Slovník vybraných pojmů

A

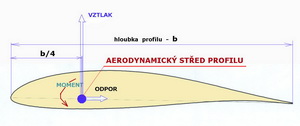
Aerodynamický střed (centrum) profilu, křídla nebo letounu je bod, ku kterému jsou momenty vznikající ze změn úhlů náběhu stálé.

Aerodynamický střed profilu se nachází přibližně v jedné čtvrtině jeho hloubky.
Aerodynamický střed křídla (nosné plochy) se nachází přibližně v jedné čtvrtině jeho střední aerodynamické tětivy.
Aerodynamický střed letounu s přirozeně fungující stabilitou by se měl nacházet vždy za jeho těžištěm.

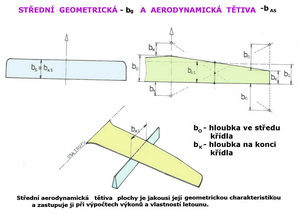
Pro dosažení stabilního letu je nutná vždy těžištní zásoba, která se pohybuje od cca 3% do 15% hloubky střední aerodynamické tětivy.

Aerodynamická tětiva je geometrická charakteristika nosné nebo ocasní plochy používaná při výpočtech výkonů a letových vlastností. Je nazývána střední aerodynamickou tětivou a obvykle je trochu větší než geometrická tětiva, která je hloubkou stejně velké obdélníkové plochy.

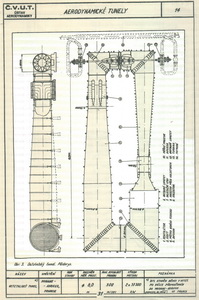
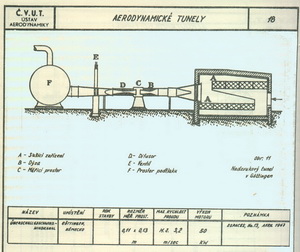
Aerodynamické tunely (AL 11/08 – Profily nosných a ocasních ploch – 5.část)

Všichni stavitelé létajících strojů a zejména jejich průkopníci v 19. století tušili a dodnes to vědí, že jejich znalosti o vztlaku a odporu nebyly a nejsou postačující. Proto začali stavět zařízení, která by jim umožnila dostat se v aerodynamice dále. Zpočátku to byly jakési „koloběhy“, kdy byly na přiměřeně velkém poloměru upevněny zkoušené předměty rotující kolem svislé osy. Toho využívali, mimo jiné, i Lilienthalové.

Pak se přišlo na to, možná, že to bylo i dříve, že by bylo možné využít nějakou“rouru“, profukovat jí vzduch a sledovat co to se zkoumaným tělesem, v ní umístěným, udělá. Tak začaly postupně vznikat větrné neboli aerodynamické tunely. Na obrázku je schéma tunelů, který používali Wrightové.

Postupem času vznikla taková monstra ke zkoumání aerodynamických vlastností profilů, křídel i celých letadel, že pro člověka neznalého dobře podstaty a cíle je jejich funkce stěží pochopitelná. Pak se přešlo od rychlostí proudů uvnitř tunelů, kolem asi 20m/s, k rychlostem přesahujícím rychlost zvuku několikanásobně a stále to pokračuje. První tunely byly v podstatě beztlakové. Průtočné nebo později cirkulační s uzavřenými nebo otevřenými měřícími prostory. Dále bylo nutno z důvodů zkoumání vlastností profilů při vyšších rychlostech než asi 150m/s přejít na tunely přetlakové.

Aerodynamickou laboratoř dnes naleznete na ploše několika tisíc metrů čtverečných a na první pohled ji nerozeznáte od nějakého průmyslového výrobního objektu. Je v ní zaměstnáno několik desítek až stovek vysoce kvalifikovaných lidí.

Následující obrázky jsou pouhým nástinem toho, co se v této branži dělo.

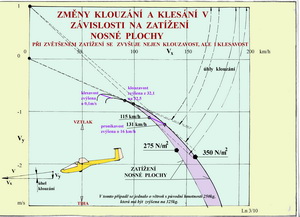
I když je dnes k dispozici mnoho výkonných počítačů a nemálo vhodných programů k získání aerodynamických charakteristik profilů, křídel i letadel jsou to stále ještě tunely, které poskytují základní i korekční informace pro navrhování létajících strojů.

B

BALAST neboli přídavná zátěž

Jednou ze zásad stavby jakýchkoliv létajících strojů je postavit je co nejlehčí.

Balast je například přidáván pro získání přechodně vyššího zatížení nosné plochy kvůli zlepšení klouzavosti při vyšších rychlostech. To využívají zejména větroně. Na přiloženém obrázku je jeden příklad rychlostních polár skutečného větroně pro dvě zatížení nosné plochy. Všimněte si, jak se zmenšily úhly klouzání (zvýšila se klouzavost) když byla zvýšena hmotnost stroje. Zároveň ale stoupla i klesavost.

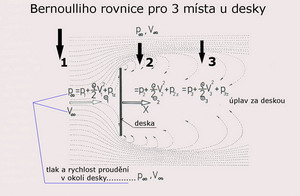
Užitečná zátěž, což mohou být pasažéři, zboží, rezervní palivo apod. charakterizuje úroveň výkonů létajícího stroje. Čím je tato zátěž větší, tím lépe pro provozovatele.

Jestliže by, ale někdo chtěl postavit letadlo s větší zátěží a použil by k tomu zbytečně mohutné konstrukce všech jeho částí, nastoupil by na špatnou cestu.

Těžší křídlo, ale i trup i ocasní plochy, má větší momenty setrvačnosti, které se projeví nepříznivě při jakékoliv změně rovnovážného pohybu ve vzduchu na pohyb nerovnovážný nebo křivočarý. Nastává to při zatáčení, zrychlování, akrobacii apod. Letové vlastnosti-řiditelnost a ovladatelnost se zhorší, což může mít velmi neblahé následky.

Pokud se však má přidávat nějaká komerční i nekomerční zátěž, se kterou je v návrhu počítáno, pak je vhodné umístit ji co nejblíže těžišti letadla. Při tom je nutné dodržet jeho polohu v mezích neohrožujících nebo výrazně neztěžujících létání stroje.

Stroje s velkou zátěží nosných ploch mohou mít určité potíže při startu a v následném stoupání. V turbulentním prostředí přijatelné intenzity jsou však ve výhodě.

Stoupání zatížených strojů je náročné na spotřebu energie a jejich pohonné jednotky musejí být dostatečně dimenzovány.

Před přistáním se mnohé stroje, ať již s užitečným zatížením (palivo) nebo jiným zatížením (vodní zátěž, bomby apod.), zbytečné zátěže zbavují, aby předešly případným poškozením při nevydařeném přistávacím manévru nebo na plochách s krátkou dráhou.

Bernoulliho rovnice

( ρ/2 ) v² + p = konst.

Bernoulliho rovnice vzešlá z Eulerovy rovnice pro, v čase ustálený, pohyb dokonalé tekutiny rychlostí V říká, že součet dynamického tlaku(první člen levé strany rovnice) a tlaku statického(druhý člen levé strany rovnice) je stálý.

Bezpilotní systémy
Unmanned Aerial Vehicles - UAV

Bezpilotní systémy nebo také prostředky jsou létající stroje bez lidské posádky, schopné plnit předem zadané a během letu doplňované či pozměňované úkoly.

Je možně je dělit do tří skupin.

Do první jsou řazeny ty jež mohou být dálkově ovládány vhodným zařízením ze Země v rozsahu viditelnosti a po splnění úkolu se vrátit zpátky.

Do druhé patří ty bezpilotní prostředky, které se mohou pohybovat obdobně jako ty předchozí, ale až za hranicí viditelnosti.

Třetí skupinu pak tvoří tzv. plně autonomní prostředky, které vyžadují vedle automatického pilota vhodný program, který jim umožňuje plnit úkoly zcela nezávisle.

Nyní jsou již dostupné takové technické prostředky, že autonomní činnost je schopen splnit i středně velký model letadla.

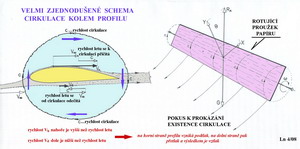
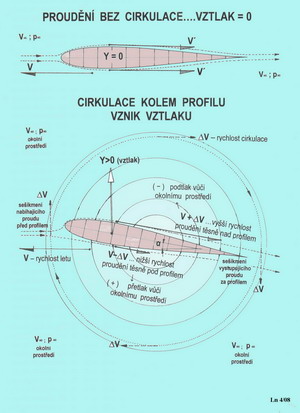
C

Cirkulace rychlosti při proudění

Tohle bude trochu náročnější na vnímání a dokonce i na přečtení. Pokusíme se představit okolnosti související s cirkulací rychlosti při proudění.

Jestliže předpokládáme, že tekutinu lze považovat za fyzikální kontinuum, tj.úplně a spojitě vyplňující daný prostor a že její nejmenší částečky mají stejné fyzikální vlastnosti jako její celek, pak jsme schopni například sledovat v určitém okamžiku stav celého proudu. Charakteristiky proudění jsou vázány na jednotlivé body uvažovaného prostoru, jemuž připisují kinematické vlastnosti.

Hmotný prvek, částice proudu, získává svoje dynamické vlastnosti teprve svým zařazením do tohoto kinematického prostoru, jež je zván rychlostním polem. V něm má každá částice proudu svoji rychlost danou její velikostí a směrem-vektorem.

Stav proudění vyjadřuje jeho proudnicový obraz. Takže ku příkladu při stálém(stacionárním) proudění jsou proudnice totožné s drahami částic proudu. S tímto stavem se nejčastěji v aerodynamice pracuje. My ho zde také využíváme.

Předním úkolem při proudění tekutin je stanovit rychlost jejich částic v libovolném bodě rychlostního pole proudu. Jsou tedy zkoumány poměrné přírůstky rychlostí částic ve třech souřadných osách. Částice se však nepohybují aniž by se při tom neotáčely. Tak vzniká vířivé pole proudění.

Jestliže bychom dokázali sečíst působení těchto vlivů na nějaké uzavřené křivce uvnitř tohoto pole, což se podařilo popsat již v 19. století např. Angličanu G.Stokesovi, tak tuto hodnotu nazýváme cirkulací rychlosti. Jedná se o výraz pro práci vykonanou vektorem rychlosti podél nějaké uzavřené křivky(a tou bude pro nás, po zjednodušení úvah, profil).

Tento jev je možné porovnat pro mnohé známým obrazcem rotačního proudění ve víru, který vznikne například ve vodě nebo při míchání kávy v šálku apod.

Jestliže vytvoříme představu, že do osy víru umístíme těleso jehož vnější tvary jsou ohraničeny uzavřenou křivkou(to je naše křídlo nekonečného rozpětí a tedy profil) vznikne kolem něho vírový pohyb a v něm se objeví cirkulace rychlosti víření. Smysl cirkulace u křídla je proti směru hodinových ručiček, nabíhá-li proud vzduchu z levé strany. Rychlost nabíhajícího proudu se nad křídlem zvětšuje o rychlost cirkulace a pod křídlem zase o ni zmenšuje. Tak dochází k rozdílným rychlostem proudění nad a pod křídlem, jejichž výsledkem je vztlak.

Před křídlem se směr nabíhajícího proudu vzduchu vlivem cirkulační rychlosti víru zvedá a za křídlem zase naopak klesá.

Aby to nebylo zase tak jednoduché, i když si mnozí čtenáři, pokud nějací byli, nejsou jisti ani tím co mohou z doposud zde sděleného využít, tak dopovím, že: cirkulace bez vztlaku, podle této teorie Žukovského a Kutty, není možná a opačně. Vztlak je tím větší, čím intenzivnější je cirkulace. A tak je to až dodnes.

Takhle nějak, jak ukazuje předchozí obrázek, to probíhá kolem profilu. V jeho pravé části je návod k uskutečnění jakéhosi ověřovacího experimentu pro přijmutí, prve, velmi kostrbatě, zjednodušeně a tím i ne úplně profesionálně vysvětlované existenci cirkulace kolem profilu.

Na dalším obrázku je učiněn pokus o zachycení cirkulace ve víru kolem křídla, který je částí vírového proudění kolem křídla konečného rozpětí.

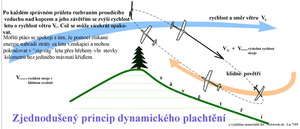
Okolnost, že na vír s cirkulací rychlosti, vázaný na křídlo v přímočarém proudění, působí vztlak má analogii v elektromagnetismu. Kolem přímočarého vodiče elektrického proudu se vytváří magnetické pole, jehož siločáry jsou kružnice kolem něj. Vytvářejí tak obrazec víru. Nachází-li se takový vodič v magnetickém poli, například mezi póly magnetu, působí na něj síla snažící se jím pohybovat napříč siločarami magnetického pole. Tato síla je analogická vztlaku.

(Tento odstavec je s malými změnami převzat z knihy Jaňour,Podzimek,Hacura – Základy aerodynamiky a mechaniky letu, r. 1953).

Pro sestavení celého tohoto povídání o cirkulaci bylo převážně použito knihy Bauer,Brůha,Jaňour- Základy proudění,Letecký průvodce 2, r.1950.

D

Dynamic soaring

Nejedná se o známý způsob létání na svahu, kdy je využíváno vzestupných proudů na jeho návětrné straně k tomu, aby byly pomocí energie větru vylepšeny aerodynamické vlastnosti letounu. Je to jiný druh létání, který je zatím provozován pouze modely letadel. Oč běží v těchto případech?

Je to ne příliš jednoduché, ale zrychlující se létání za silnějšího větru vanoucího příčně ke vhodnému svahu. Jeho závětrná strana má mít výrazně klesající tendenci a vytvářet tak přiměřeně hluboké údolí v němž je možné vykonat zatáčku o 180^o. V podstatě jsou to zatáčky na malém poloměru a s úhlem náklonu přes 80^o. Čím je vršek svahu ostřejší, tím jsou podmínky pro tento druh plachtění příznivější.

Vichr hrnoucí se po svahu vzhůru vytváří na jeho návětrné straně vzestupná proudění.

Zde je nutno letět proti větru a jak již víme je nutné při tom změnit seřízení nosné a vodorovné ocasní plochy, aby se větroň dostal kupředu. To je první letový prostor.

Druhý prostor, nabízející se k využití pro plachtění, je šikmo dole za svahem, v jeho údolí. Zde větroň může letět ve směru větru v celkem klidném ovzduší.

Jaký je asi princip?

Model vypuštěný na hřebeni svahu začne stoupat vlivem vzestupného proudění na jeho návětrné straně. Po ulétnutí určité vzdálenosti se otočí o 180^o a letí zpátky ke svahu po větru. Jeho rychlost nyní vzrostla teoreticky o rychlost vanoucího větru. Po přelétnutí hřebene svahu se ponoří do údolí s touto zvýšenou rychlostí kde panuje celkem poklidné povětří. Pak následuje další velmi ostrá zatáčka o 180^o a let zpátky ke svahu směrem vzhůru k jeho hřebenu takže jeho původní rychlost je nad hřebenem svahu vyšší skoro o rychlost větru.

Celý cyklus je možno podle libosti nebo až do úplného zničení stroje opakovat. Viz následující obrázek.

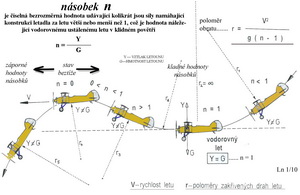
Po nějaké době se ukázalo, že i po pevnostní stránce vypiplané stroje tomuto způsobu létání nestačí. Takže bylo přikročeno k ještě robustnějším konstrukcím, větším zatížením nosných ploch, někdy i ke zvětšení rozměrů a k využití některých jiných profilů.

Kompozitové konstrukce se značným množstvím uhlíku ve všech částech modelu jsou nezbytností.

V současné době, tj. v první polovině roku 2009 je při tomto způsobu létání dosahováno s modely větroňů rychlostí větších než 600km/h.

L

Letové vlastnosti

Každý letoun musí vykazovat vedle požadovaných nebo vysněných výkonů ještě schopnost být v dostatečné míře řiditelný a současně stabilní.

Letové vlastnosti letounu zahrnují jak jeho stabilitu tak i řiditelnost, které jednak umožňují dosažení předpokládaných výkonů a současně zajišťují jeho bezpečný provoz.

Když má letoun dostatečnou schopnost vracet se, pomocí svých vlastností, po každé menší poruše dráhy letu do předchozího ustáleného pohybu pak je dynamicky stabilní.

Jestliže je nutné převést letoun z jednoho ustáleného stavu letu do druhého, k čemuž poslouží otáčení kolem některé ze tří jeho os, pak mluvíme o řiditelnosti.

Jaký je rozdíl mezi stabilitou a řiditelností? U dynamicky stabilního letounu je patrná snaha zaujmout předchozí ustálenou polohu automaticky díky jeho aerodynamickým charakteristikám. Pilotův zásah není vyžadován pokud není porucha stavu výrazná. Jestliže ale oprava letového stavu vyžaduje zásah pilota a tím změnu sil a momentů působících za letu, pak se jedná o řiditelnost.

Řiditelnost letounu zahrnuje v sobě ovladatelnost, obratnost, vyvažitelnost a tíživost.

Ovladatelnost je posuzována jako možnost pohybovat se ustáleným letem pomocí hlavních řídících prvků stroje. Při tom se jedná o ovladatelnost:

-podélnou, to jest takovou, jak velkého rozsahu letových rychlostí je schopen letoun dosáhnout v ustálených letech pomocí výškového kormidla při zvoleném výkonu pohonné jednotky, při nějaké poloze vztlakových klapek apod.

-stranovou, jež udává při daném výkonu pohonné jednotky( za symetrického tahu) jak velkého rozsahu příčného náklonu, úhlu vybočení a sklonu dráhy letu je možné docílit z přímočarého letu(popsaného rychlostí, tahem pohonů a polohy letounu) účinkem směrového kormidla a křidélek. U vícemotorových letounů je to schopnost letět ještě přímočaře při nejmenší rychlostí a nesymetrickém tahu pohonu.

Obratnost je schopnost letounu uskutečňovat různé obraty a přecházet z jednoho ustáleného stavu do jiného zvolenou rychlostí a otáčet se kolem všech tří os letounu v mezích maximálně přípustných sil a výchylek řídících prvků.

-integrální obratnost udává v jakém čase je možné uskutečnit nějaký obrat(přemet, zatáčku, výkrut,..)

-elementární obratnost popisuje jak rychle je možné s letounem přejít z jednoho ustáleného stavu letu do jiného

-úhlová obratnost(rotace kolem jedné ze tří os aerodynamické soustavy letounu) udává jak velké úhlové rychlosti je možné dosáhnout náhlým zásahem do řízení. Při tom je posuzováno nejen dosažení maximální možné úhlové rychlosti, ale i to jak rychle letoun na zásah pilota reaguje. Mluví se také o „poslušnosti“ letounu.

Vyvažitelnost je vlastnost při níž je možné vhodnou úpravou(zařízením) odstranit trvale působící sílu v řízení, která může obtěžovat pilota. Vyvažitelný má být každý ustálený let, jestliže probíhá déle než asi 5 minut. Při tom nesmí dojít k porušení rovnováhy daného ustáleného letu.

Tíživost souvisí se změnami sil v řízení nebo změnami ustálených stavů, jestliže se změní například poloha těžiště, vysune(zasune) se podvozek, změní se úhly nastavení klapek nosné plochy, výkon pohonné jednotky nebo vybočení letounu z přímého směru letu.

Neopomenutelnou pozornost vyžaduje stav kdy dochází k náhlé změně výsledné aerodynamické síly na nosné ploše. Po překročení kritického úhlu náběhu dojde k náhlému odtržení proudu vzduchu-obvykle na horní straně nosné plochy a to během několika desetin sekundy.

Pak je tu ještě potřeba optimalizace ve spolupůsobení letových vlastností.

Protože letové vlastnosti jsou výsledkem správného fungování všech částí letounu a působením jeho hmot vzhledem k těžišti, musí být jejich účinky posuzovány společně. Některé aerodynamické a geometrické charakteristiky letounu se sice vzájemně příznivě mohou ovlivňovat jiné však působí proti sobě. Tak například posunutí polohy těžiště směrem k náběžné hraně nosné plochy sice zajistí větší míru podélné stability, ale zhorší ovladatelnost a také výkony, protože letoun se nepohybuje po dobu tohoto letu v okolí nejvhodnějšího úhlu náběhu. Nebo srázový úhel za nosnou plochou může při její nevhodné vertikální poloze neblaze ovlivňovat funkci VOP. A podobně.

Důležitá je i znalost proměnlivosti letových vlastností. Ta se sice nemusí týkat každého stroje každodenně, ale je třeba zvážit například proměnlivost při létání v různých výškách, při různých teplotách, při deformacích povrchů(déšť, námraza), změnou Reynoldsova a Machova čísla, přehřátí motorů, atd, atd.

N

Násobek

Jestliže se letoun pohybuje v ovzduší Země působí na něj následující síly:

• hmotnost – je to stále stejná síla působící směrem ke středu Země
• aerodynamické síly – se během letu mění, protože jsou závislé na rychlosti letu a postavení letounu vůči směru jeho pohybu. Je to především vztlak a odpor, které jsou převážně doprovázeny ještě klopným momentem.
• síly od pohonu – které vnáší do letounu pohonná jednotka a vyvolává ještě reakční a gyroskopický moment. Nezanedbatelné síly se přenášejí na bezmotorový letoun i při startu pomocí navijáku či aerovleku.

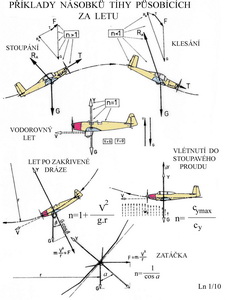
Tyto tři skupiny vnějších sil působí na letadlo při ustáleném rovnovážném letu, tj. tehdy kdy letadlo letí přímým letem a ani nezrychluje nebo nezpomaluje.

Když se ale letadlo nepohybuje ustáleným přímočarým pohybem, což je skoro vždy, dochází k působení dalších sil a momentů. Původní rovnováha letu se poruší a letadlo se snaží zachovat stav pohybu před započetím těchto dalších, nově vzniklých, sil. Tato snaha letícího stroje se projevuje jako jeho setrvačná síla a její velikost je dána součinem jeho hmotnosti a okamžitého zrychlení pohybu. Tak vstupují do soustavy doplňkové síly.

Jakmile se změní tvar dráhy letu, s čímž souvisí i změna rychlosti a postavení letadla, vznikne doplňková síla i moment. Ty mohou několika násobně převýšit hmotnost letounu a porovnávají se se zatížením působícím na ně v ustáleném vodorovném letu, kdy je v rovnováze celkový vztlak letadla s jeho tíhou. Tento poměr zatížení je nazýván násobkem.

Jeho smysly působení mohou být vzhledem k zemskému středu opačného směru. Tj. mohou působit nahoru i dolů. Pak mluvíme o násobcích kladných nebo záporných. Všechny důležité části létajícího stroje jsou pak navrhovány pro namáhání poněkud vyšší s koeficientem větším než 1. Tomuto koeficientu se říká jistota, o kterou je provozní násobek zvětšen.

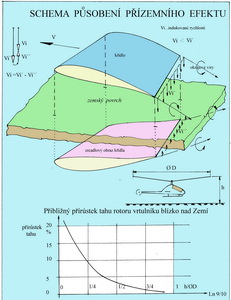
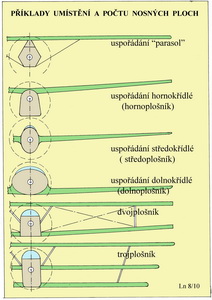
Maximální hodnoty násobků pro jednotlivé skupiny letounů a jejich předpokládaný letový provoz jsou určeny příslušnými předpisy a musí být při jejich projektování respektovány a jednotlivé části i příslušenství letounů na ně, včetně nezbytné rezervy, dimenzovány.

Totéž platí pro osádky letounů, aby nedocházelo ke snižování jejich fyzických a psychických schopností nutných pro řízení nebo dokonce k poškození jejich zdraví.

Podrobnější text v Akademii letectví 4/10.

P

Přízemní efekt

Pokud se pohybují letouny v malé výšce nad Zemí tak se při tom uplatňuje tak zvaný přízemní efekt, kdy křídlo pohybující se nad Zemí ve výšce menší než jeho rozpětí má menší indukovaný odpor a proto lepší výkon. To platí například také pro vrtulníky a vírníky, když jsme to již určitě pozorovali u ptáků,

Jedná se o okrajové víry vznikající na křídlech konečných rozměrů. Přetlak pod křídlem se snaží na jeho koncích proniknout do tlaku nižšího nad křídlo za vzniku intenzivních vírů. Ty způsobí odklonění výsledné vztlakové síly směrem proti letu a jeho složka tak vytváří přídavný odpor, tzv. indukovaný. Ten je přímo závislý na velikosti vztlaku, štíhlosti a půdorysném tvaru křídla.

V blízkosti zemského povrchu (pevná půda nebo vodní hladina) je nepříznivý účinek těchto vírů zmenšován, takže klouzavost se zvětšuje a klesavost se zmenšuje.

Příklady mohou být následující:
-jestliže se letoun s pevným křídlem pohybuje ve výšce menší než je polovina jeho rozpětí pak je možné očekávat zlepšení jeho výkonů alespoň o 10%
-u vrtulníků a vírníků má malá vzdálenost od zemského povrchu na průběh tahu jejich rotorů také podobný příznivý účinek.

Konečný rozměr rozpětí křídla letounu, společně s jeho tvarem, je příčinou okrajových vírů. Ty vytvářejí sešikmení proudu za křídlem směrem dolů a v důsledku toho mění jeho původní úhel náběhu o indukovanou složku. Sešikmený směr rychlosti proudu za křídlem je geometrickým součtem původní rychlosti letu V a t.zv.indukované rychlosti Vi, jak je patrno z obrázku.

Proud přichází ke křídlu nyní pod menším úhlem. Vztlak jakožto síla kolmá na směr příchozího proudu vzduchu je nyní odkloněn dozadu o indukovaný úhel náběhu a svojí složkou vytváří přídavný– indukovaný, odpor.

Horní část obrázku využívající vírové teorie křídla zjednodušeně graficky ukazuje, že původní indukovaná rychlost křídla Vi´ se zmenší o indukovanou rychlost Vi´´ virtuálního, zrcadlově umístěného, křídla pod ním. Jejich geometrickým součtem je výsledná indukovaná rychlost Vi skutečného křídla, která je menší původní než Vi´ náležející letu ve volné atmosféře, tj. za letu alespoň ve výšce rovné rozpětí křídla nad Zemí.

A konečným efektem je pak mírné zvýšení vztlaku za současného snížení indukovaného odporu, což zlepšuje výkony letounu. To jsou výhodné okolnosti při startech a obvykle i při přistáních letounů, vrtulníků a vírníků (viz spodní část obrázku).

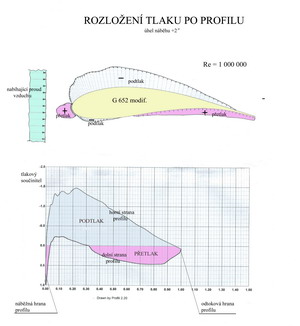
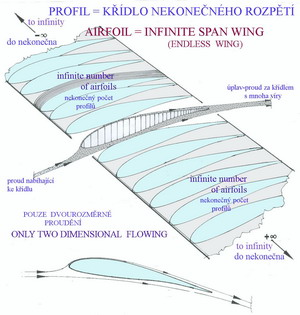
Profily nosných a ocasních ploch, ale i listů vrtulí a rotorů.

Co je to profil?

Profil je uzavřená rovinná křivka vzniklá řezem nosné či ocasní plochy a také listem vrtule nebo rotoru (a rovněž lopatkou rotačního stroje) v rovině kolmé na jejich podélnou osu.

Protože profil je pouze rovinným obrazcem nelze mu přiřazovat vlastnosti jimiž jsou vztlak, odpor, moment apod. Proto jej nahrazujeme při dalších úvahách pojmem křídla nekonečného rozpětí, u něhož již můžeme na důsledcích dvourozměrného obtékání kolem něj posuzovat jeho aerodynamické vlastnosti. Příklad křídla nekonečného rozpětí je na obrázku.

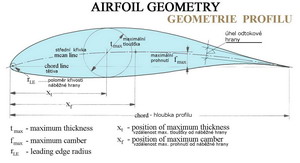
Abychom mohli porovnávat vlastnosti jednotlivých profilů je třeba je nějak geometricky popsat. Samotný tvar křivky nám nestačí. Proto je obrys profilu popsán vhodně zvoleným počtem souřadnic v pravoúhlém systému, které definují jeho tvar. V některých případech má souřadný systém počátek vlevo(na náběžné hraně) v jiných zase vpravo(na odtokové hraně). Na dalším obrázku je schéma profilu v souřadném systému s uvedením některých dalších geometrických charakteristik.

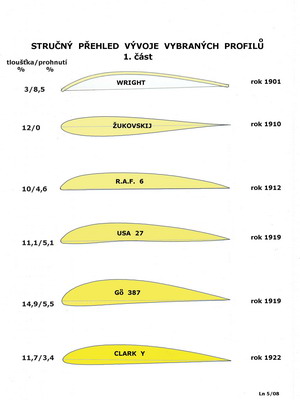
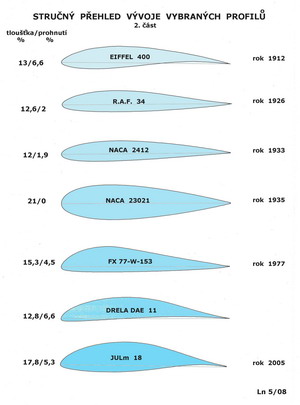
V předchozím obrázku jsou uvedeny zbývající základní geometrické charakteristiky profilu, které je vhodné pochopit a porozumět jim.

Jednotlivá letadla určená k různým účelům využívají přirozeně i profilů s různými tvary a vlastnostmi. Jeden profil není schopen vyhovět úspěšně zcela rozdílným požadavkům létajících strojů.

Na dalších dvou obrázcích je velmi stručně a nekompletně uveden pokus zachytit jakýsi vývoj profilů od počátku 20. století dodnes, pro oblast nižších rychlostí letu, dejme tomu do 450km/h.

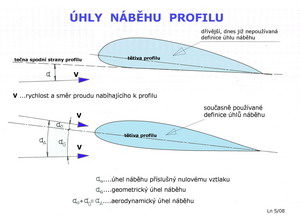
Aerodynamické vlastnosti profilů závisí nejen na jejich tvaru, ale také, mimo jiné, na poloze vůči směru letu. Tato skutečnost je vyjadřována úhlem, který svírá tětiva profilu se směrem letu(nebo jinak řečeno se směrem proudu nabíhajícího k němu). V aerodynamické praxi se obvykle lze setkat se třemi pojmy úhlů náběhu:

1.úhel náběhu při nulovém vztlaku profilu, který je pro prohnuté profily vždy záporný, ale pro souměrné profily je vždy roven nule

2. úhel náběhu sevřený mezi tětivou profilu a směrem letu, je to tzv. geometrický úhel náběhu. Ten může mít hodnoty kladné i záporné

3.konečně je to aerodynamický úhel náběhu, který je součtem obou dvou předchozích hodnot.

Všechny tyto úhly jsou na následujícím obrázku uvedeny. Je zde ještě připomínka dřívějšího způsobu vyjadřování úhlu náběhu profilu, který byl ale opuštěn kvůli nemožnosti jednotného posuzování různě tvarovaných profilů.

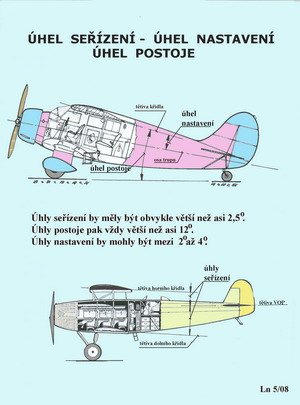
Pak jsou to ještě jiné úhly související s polohou profilu nosné plochy vůči létajícímu stroji na němž je použit. Viz další obrázek.

Jsou to následující pojmy, které by měly být používány s plnou zodpovědností k důležitostem, jaké zaujímají při návrhu letadla.

a)úhel nastavení je ten úhel, který svírá tětiva křídla s osou trupu

b)úhel seřízení je ten, který svírají tětivy křídla(křídel) s tětivou VOP

c)úhel postoje na Zemi je tím úhlem, který umožňuje využít co nejvyšší součinitele vztlaku při startu a přistání, aby k tomu potřebná dráha nebyla tak dlouhá a rychlosti, zejména při přistání, nepřiváděly posádku v úžas nad tím co mají ovládat.

Proudění laminární a turbulentní

Jestliže se pohybují částice proudu tak, aby se jejich dráhy nekřížily, tak pro takovýto druh proudění používáme názvu laminární. Je to proudění v tenkých vrstvách vzájemně se nemísících, takže se používá pro ně také pojmu – vrstevnaté proudění. Tento druh proudění se vyznačuje nízkým odporem, pokud jsou pro jeho vznik dodrženy nezbytné podmínky. Je ale také dost nestálé a když mu do cesty vstoupí nějaké překážky-zvětšená drsnost povrchu, prudká změna tvaru apod., ztratí svůj původní charakter a tím i svoji výhodu nízkého odporu.

Když se však částice proudu pohybují neuspořádaně, jejich dráhy se navzájem kříží, je takové proudění nazýváno prouděním turbulentním. Odpor těles tímto proudem obtékaných je oproti laminárnímu větší. Tento druh proudění má ale stálejší charakter a je schopen proudit kolem drsnějších povrchů, i těch co mění svůj tvar významněji, úspěšněji než proud laminární. Je to dáno hlavně příznivě působícími dynamickými účinky částeček proudu, které jsou odvozeny od jejich rychlostí.

V mnoha případech může být výsledný odpor turbulentního proudu nižší než u vynucovaného proudu laminárního.

Jestliže nastane laminární obtékání nějakého tělesa, čemuž dochází v jeho přední části prakticky vždy, pokud není výrazně zdrsněna či nevhodně tvarově deformována, přechází laminární proudění na nějaké části povrchu tělesa v proudění turbulentní. Pokud k tomu dochází, je možné postupně pečlivě tvarovat toto těleso a současně zjemňovat jeho povrch, s cílem prodloužit laminární proud co nejdále. Mnohdy tomu však tak není. Laminární proud se nestačí změnit v přilehlý proud turbulentní a od povrchu tělesa(nosné nebo ocasní plochy) se odtrhne. Vznikne tak obrovský nárůst odporu, který předchozí úsilí, o vytvoření co nejmenšího odporu vlivem využití laminárního proudu, zcela zhatí.

Na připojeném obrázku je schéma laminárního a turbulentního proudění, na příkladu rovné desky postavené rovnoběžně se směrem proudu, ukázáno.

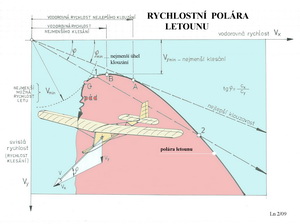
R

Rychlostní polára

Rychlostní poláru letounu sestrojíme tak, že pro jednotlivé fáze jeho letu spočítáme pomocí jeho aerodynamické charakteristiky z celkové rychlosti letu V rychlost vodorovnou V_x a rychlost svislou V_y.

Vodorovná rychlost popisuje pohyb letounu podél zemského povrchu a svislá rychlost zase pohyb směrem k němu(klesání) nebo od něho(stoupání). Předpokládá se nehybná okolní atmosféra, což se v praxi takřka nestává, jak jsme již naznačili v některých dřívějších článcích.

Obě prve spočítané rychlosti vyneseme do grafu, jehož příklad je v následujícím obrázku.

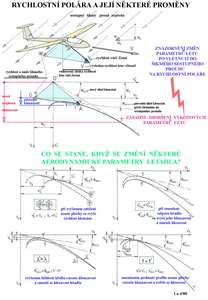
Silně vytažená čára je rychlostní polára letounu s několika vyznačenými body na ní.

Vedeme-li z počátku souřadnic tečnu k této křivce získáme v bodě dotyku A údaj pro rychlost letu při níž je dosahováno nejlepší klouzavosti. Ve všech ostatních případech je klouzavost horší.

Vedeme-li k poláře tečnu vodorovnou dospějeme v bodě B k rychlosti letu při níž je dosahováno nejmenší klesavosti.

Postupujeme-li po poláře dále vlevo dostáváme se k bodu G, který označuje nejmenší možnou, ještě bezpečnou rychlost letu. Pokusy o její další zmenšování vedou k odtržení proudu od nosné plochy letounu a k jeho pádu.

Pak jsou tu ještě body 1 a 2 na poláře. Jejich spojnice ukazuje příklad jak je možné při stejné klouzavosti letět dvěma různými rychlostmi.

Čím je sestupná pravá část poláry strmější tím horší je pronikavost letounu v povětří v němž se nachází.

Ještě je tu následující obrázek s některými účinky změn prostředí i aerodynamických a geometrických charakteristik letounu na podoby rychlostní poláry.

Z příkladů ve spodní části obrázku je možné získat představu o tom jak se změní některé aerodynamické parametry letounu, když se zvýší zatížení nosné plochy, zmenší odpor , zvýší štíhlost křídla nebo použije profil s jiným prohnutím.

S

Stabilita letounu

Pro pohyb letounu platí obvykle pohybové rovnice dle Newtonových zákonů. Pokud se stroj pohybuje rovnoměrně a přímočaře jsou všechny na něj působící síly v rovnováze a jejich součet je nulový. Pokud tomu tak není vzniká za pohybu letounu další doplňková síla. Ten při tom mění buď rychlost nebo se pohybuje po zakřivené dráze nebo koná obojí najednou. Tím se zabývá mechanika letu, která řeší výkony a letové vlastnosti létajících strojů, mezi jinými i stabilitu letu.

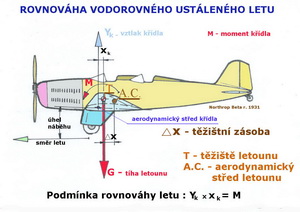
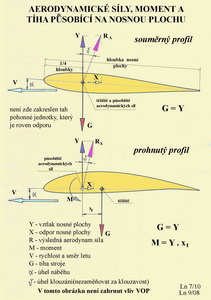
Na tomto obrázku jsou schematicky zachyceny tři hlavní skupiny sil působících na letící stroj.

Z gravitačních sil je to tíha letounu - G.

Ze sil vzniklých vlivem prostředí je to výsledná aerodynamická síla – RA.

Ze sil od hnací skupiny je to tah – T.

Pak je tu ještě uvedena rychlost a směr letu – V a doplňkové síly – Z, které jsou právě tak velké, aby uzavřely silové obrazce, kdy je dosaženo momentálního rovnovážného stavu.

Vlevo nahoře je to grafický součet vektorů těchto sil – G, RA, T a F. Doplňková síla F vzniklá změnou tvaru dráhy letu způsobila, že letoun klesá. Aby tomu bylo zabráněno je třeba buď zvětšit výslednou aerodynamickou sílu RA nebo zvětšit tah T nebo obojí.

Vpravo dole je jiný silový diagram, kdy geometrický součet gravitace, výsledné aerodynamické síly a tahu dovoluje letounu stoupat. Jak a kterým směrem ukazuje vektor síly F.

V dalším obrázku jsou dvě schemata působení aerodynamických sil a sil tíže v rovnovážném letu a sice pro profil souměrný(nahoře) a pro profil prohnutý(dole).

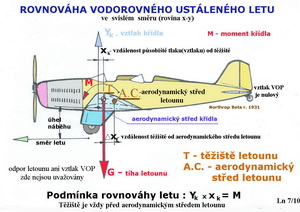
U profilu souměrného je těžiště letounu při rovnoměrném vodorovném přímočarém letu velmi blízko aerodynamickému středu nebo je s ním totožné.

Kdežto u profilu prohnutého, kde již působí klopný moment M, je těžiště letounu za aerodynamickým středem nosné plochy (1 hloubky střední aerodynamické tětivy). Ne však za aerodynamickým středem letounu.

Tím je, ve vodorovném přímém ustáleném letu, vlivem účinku dvojice sil Y(vztlak) a G(tíha) kompezován účinek klopného momentu, takže nedochází ke klopení(otáčení podle příčné osy letounu). Všimněte si, že vztlak VOP je zde nulový.

Ale kam umístit těžiště letounu, aby takový let byl zajištěn?

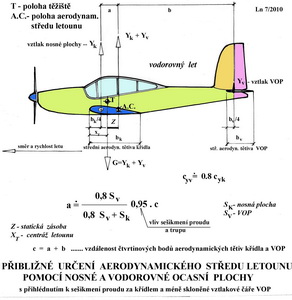
Z předchozího obrázku je patrné, že aerodynamické centrum nosné plochy je asi ve 1 její střední aerodynamické tětivy(to již víme z dřívějška). Zde působí její odpor a vztlak jejichž součtem je výsledná aerodynamická síla.

Za ním se v určité vzdálenosti nachází těžiště letounu, jehož polohu ovlivňuje VOP zásadním způsobem. V případě, že klopný moment nosné plochy působí v uvedeném smyslu, je jeho vzdálenost od 1 bodu střední aerodynamické tětivy křídla úměrná velikosti klopného momentu.

Když bude klopný moment nulový bude se nacházet těžiště letounu velmi přibližně v 1 střední aerodynamické tětivy.

Jestliže ale bude mít klopný moment opačný smysl působení je nutné posunout těžiště letounu před 1 hloubky střední aerodynamické tětivy.

Kde se nachází aerodynamický střed letounu?

Aerodynamický střed nosné plochy se nachází ve cca 25% její střední aerodynamické hloubky.

Jestliže k nosné ploše přiřadíme další části letounu – trup, motorové gondoly, podvozek,... posune se jeho A.C. mírně dopředu.

Když však ale přiřadíme k nosné ploše ještě VOP – vodorovnou ocasní plochu(nepleťte si ji s výškovkou, protože to je jen její pohyblivá část) posune se A.C. letounu dozadu od A.C nosné plochy.Viz následující obrázek.

Je v něm vyjádření vlivu velikosti a polohy VOP na polohu A.C. letounu. To má významný vliv na posun A.C. směrem dozadu od 1 bodu střední aerodynamické tětivy nosné plochy.

Tento příznivý účinek VOP je ještě větší, když VOP není umístěna za nosnou plochou v oblasti sešikmení proudu.

Ještě je nutné počítat počítat s vlivem obvykle menší štíhlosti a také menšího Re čísla u ní.

Takže jestliže známe velikost nosné plochy, velikost VOP a jejich vzájemnou polohu můžeme, při prve uvedených předpokladech, stanovit přibližnou polohu A.C. letounu podle vztahu uvedeného v předchozím obrázku.

Stabilita:

Stabilitu letounu můžeme rozdělit do několika skupin a posuzovat letové vlastnosti v podélném pohybu(podél osy příčné), v pohybu směrovém(podél osy svislé), v pohybech příčných(kolem osy podélné) a konečně v pohybech stranových(současně podél osy podélné a svislé).

Každý letoun může být dostatečně, málo, vhodně nebo vůbec ne stabilní.

Stabilita podélná souvisí s pohyby letounu kolem jeho příčné osy . Zde mají rozhodující význam klopné momenty vzhledem k těžišti, které určují do jakého úhlu náběhu se letoun nastaví během letu. Viz další obrázek.

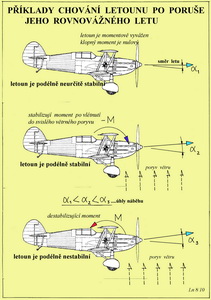
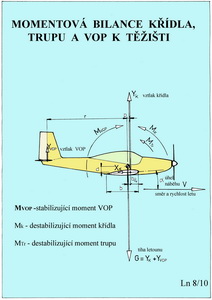
V horní části obrázku je pokus znázornit letový stav AVIE jakožto momentově vyvážený. Výsledný moment letounu k těžišti je nulový a letoun se pohybuje rovnovážným ustáleným letem.

Ale jen tak dlouho dokud nedojde k nějakému vnějšímu podnětu, například při vlétnutí do svislého větrného poryvu. To je znázorněno uprostřed obrázku.

Letoun okamžitě zvětší úhel náběhu svého pohybu a má snahu stoupat a zpomalovat let. To je obvykle nejen nežádoucí, ale i nebezpečné. Jestliže za této situace vznikne na letounu klopný moment ( zde se znaménkem minus – těžký na hlavu) snažící se ho navrátit do původního letového stavu pokládáme letoun s takovouto vlastností za stabilní. Poloha těžiště je vždy před A.C. letounu ( ve směru letu).

Když však takovýto klopný moment nevznikne, bude mít letoun snahu se pohybovat v novém letovém režimu nastálém po vnější poruše. Nebude tedy ani stabilní ani nestabilní. Bude se chovat indiferentně,t.j. nevyzpytatelně. U tohoto letounu, ve srovnání s předchozím „hodným“ strojem, budou polohy těžiště a A.C. velmi blízké a nepřesáhnou zřejmě 0,5% střední aerodynamické hloubky jeho nosné plochy.

Pokud, ale vznikne na letounu za prve zmíněné situace vlivem vnějšího podnětu, klopný moment (zde se znaménkem plus) snažící se vzniklý nárůst úhlu náběhu dále zvětšovat, takže o návratu do původního stavu nemůže být ani zmínky, pak je takovýto letoun nestabilní. To je zachyceno ve spodní části předchozího obrázku.

Vezměme ještě na pomoc následující obrázek, kde jsou uvedeny případy působení třech důležitých částí letounu. Z hlediska výkonů již víme, že to je hlavně nosná plocha, která je ovlivňuje, ale teď nemluvíme o výkonech. Abychom jich dosáhli musíme mít letoun ještě s nezbytnými letovými vlastnostmi. A jednou z nich je podélná stabilita.

Pro dosažení potřebné míry stability není nejdůležitější nosná plocha (křídlo), ale je to VOP (vodorovná ocasní plocha) jinak zvaná též stabilizátor ( nikoliv však výškovka, jak stále mnozí používají). A proč tomu tak je může být patrné z následujícího obrázku.

Z obrázku lze poznat, že klopný moment VOP má opačný smysl působení než destabilizující klopivé momenty křídla a trupu.

Chceme-li tedy využít přízivého působení klopného momentu VOP ke stabilizaci letu v podélném směru, musíme ji umístit do vhodné vzdálenosti za nosnou plochou a vybavit ji potřebnou velikostí. Poměříme-li její plošnou velikost s nosnou plochou a rameno na němž působí se střední aerodynamickou tětivou nosné plochy, získáváme bezrozměrný údaj zvaný mohutnost VOP.

A nyní ještě pohled na podélnou stabilitu odjinud. Na dalším obrázku je diagram na jehož svislou osu je vynášen součinitel celkového klopného momentu letounu – mz a na osu vodorovnou úhel náběhu letounu -?.

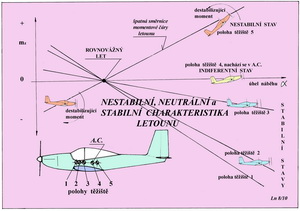
Z něj můžete pochytit, že součinitel klopného momentu samotného trupu se se zvětšujícím se úhlem náběhu posouvá k větším hodnotám.

Pro samotné křídlo je průběh obdobný.

Obojí vede k větší a větší snaze pohyb destabilizovat.

Pro naše úvahy je teď důležitá poloha těžiště a proto je klopný moment letounu, zde zmiňovaný, vztahovaný k jeho těžišti.

Co je ze stále stejného diagramu zcela zřetelné je to, že momentová čára VOP má opačnou směrnici (sklon) než samotný trup nebo samotné křídlo. Takže v části diagramu nad osou úhlů náběhu se kladný klopný moment VOP se zvětšujícím se úhlem náběhu sice zmenšuje, ale při tom působí příznivě směrem k obnově původního stavu letu.

Pod osou úhlů náběhu se klopný moment zvětšuje, ale má opačný smysl než prve. Náhle zmenšený úhel náběhu se tak snaží zvětšovat, aby bylo dosaženo jeho původní hodnoty, která je v průsečíku momentové čáry (přímky) s vodorovnou osou.

Obojí má za následek snahu obnovit původní letový stav. VOP na vhodném rameni tedy působí z hlediska stability nesmírně příznivě.

A nakonec je tu křivka(přímka) poslední a ta platí pro kompletní letoun - trup, křídlo i VOP. Její sklon je o něco menší než sklon VOP, ale účinky na podélnou stabilitu letounu jsou obdobné. Protíná osu úhlů náběhu v místě, kde se nachází rovnovážný stav letu letounu.

Na stejném typu diagramu jako prve předvedeme, jak to asi dopadne pro několik případů stabilitních stavů letounu.

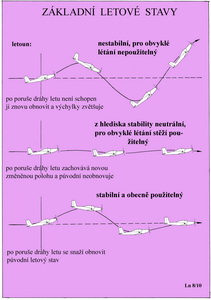
Poloha těžiště č. 5: mohutnost VOP nestačí na to, aby změnila tuto nepříznivou stabilitní charakteristiku letounu vzhledem k této poloze těžiště – leží až za A.C. Letoun je pro obvykle létání nejen nepoužitelný, ale i nebezpečný pro osádku i okolí.

Poloha těžiště č. 4 v A.C.: letoun je již sice schopen letu, ale pilotovi (modeláři) jeho úlohu v řízení nijak neusnadňuje, protože kam se naklopí, ale i nakloní, tam jeho poloha setrvá tak dlouho dokud nepřijde nějaký vnější podnět nebo zásah pilota. Změny polohy jsou velmi prudké a velké. Pro obvyklé létání, nedoporučený stav.

Poloha těžiště č. 3: ta je zjevně před polohou A.C. Letové vlastnosti takovéhoto letounu jsou již prakticky použitelné a závisí jen na jeho provozovateli jak daleko před A.C. nebo jak blízko k němu těžiště umístí.

Polohy těžiště č. 2 a 1, označují polohy těžiště ještě blíže náběžné hraně křídla než prve a podélné stability je dost a dost. Jenže v případě 1 až příliš, což se nepříznivě projeví na letových vlastnostech i výkonech. Letoun se sice pohybuje vzduchem, ale jeho pohyb je těžkopádný a nemotorný.

V dalším obrázku je schema velmi pravděpodobných pohybů letounu, jestliže je jeho stabilita nedostatečná (nahoře) nebo neutrální (uprostřed) a nebo dostatečná (dole) a pro obvyklé létání vhodná.

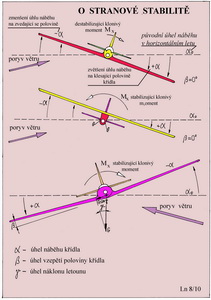
Stabilita stranová:

Při posuzování stranové stability nemůžeme pojednávat odděleně o pohybech zatáčivých, klonivých a bočivých neboť na sebe navazují a musíme je podrobit zkoumání z hlediska dynamické stability.

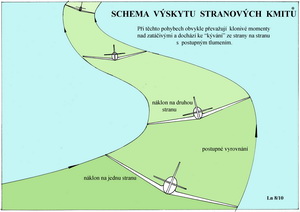
Jedním z typických stranových pohybů jsou stranové kmity. Častěji než u skutečných letounů dochází k tomu jevu u modelů letadel či UAV. Co se stane nebo může stát po náhodném naklonění létajícího stroje?

Je-li stabilizující klonivý moment, po předchozím letu s vybočením, příliš velký ve srovnání s momentem zatáčivým, dojde k prudkému vyrovnávání náklonu. Stroj pak přejde přes původní horizontální polohu do opačného náklonu a celý jev se může periodicky opakovat. Přitom vlivem současného působení zatáčivých momentů stroj mění směr letu. Schematicky je tento jev zachycen v následujícm obrázku.

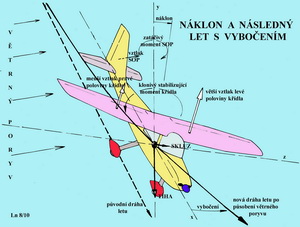
Dá se prokázat, že na nestabilitě stranových kmitů se výrazně podílí velký klonivý moment vzniklý při vybočení a nedostatečná snaha udržet původní směr letu. Příčinou je zbytečně velké vzepětí nosné plochy a malá SOP. Působí zde proti sobě vlivy vzepětí a velikost VOP.

Při létání existují ještě jiné nebezpečné letové stavy související se stranovou stabilitou. Jejich příčinou je spirální nestabilita.

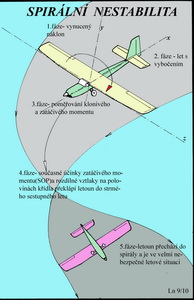
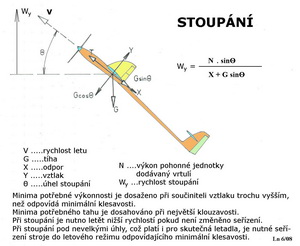
Všechny letouny i modely mají tendenci vykazovat nějakou míru této nemilé letové vlastnosti, přestože mnohé z nich mají dostatek vlastní(inherentní) stability.

Ke spirální nestabilitě přispívá příliš velká SOP a malé vzepětí křídla. To je v případech kdy je statická směrová stabilita mohutná ve srovnání se schopnostmi letounu vyrovnávat příčné náklony. Nebezpečí vzniku tohoto stavu je častější při letech s velkým úhlem náběhu.

Jestliže je stranová stabilita letounu(modelu) porušena vnějším zásahem, třeba větrným poryvem, pak následný let s vybočením se snaží mohutná SOP natočit do původního směru. Nedostatečné vzepětí křídla se sice současně, ale nesměle snaží znovu nabýt příčné rovnováhy. Polovina křídla nacházející se při tomto kombinovaném pohybu se na vnější části zatáčky pohybuje rychleji než ta druhá vnitřní část. Výsledkem je rozdíl vztlaků mezi vnější a vnitřní polovinou křídla a tím větší náklon do zatáčky. Zároveň působí v tomto smyslu nepříznivě i SOP a letoun přechází do strmého klesavého spirálního letu.

Celá záležitost může být zhoršena také nesprávnou polohou těžiště.

Stoupání létajícího stroje

Stoupavý let je jedním z manévrů létajících strojů, je-li k dispozici přebytek výkonu pohonné jednotky.

Pro dosažení ustáleného stoupavého letu je třeba zachovat rovnováhu působících sil. V podstatě se při stoupání jedná o zvedání letounu do výšky požadovanou rychlostí stoupání a zároveň o překonávání odporu při tomto letu vznikajícím. Obvykle se stoupání posuzuje při nějakém úhlu stoupání, kterému při dané výkonnosti odpovídá určitá rychlost letu.

Na připojeném obrázku jsou vzorec pro výpočet rychlosti stoupání pro zvolený úhel a k tomu nezbytný komentář, zachyceny.

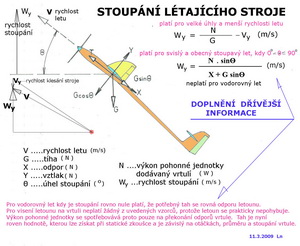
Stoupání létajících strojů - doplněk

Tento krátký vzkaz související se stoupáním létajících strojů zveřejňujeme proto, že se vyskytly celkem oprávněné připomínky, čemuž jsme rádi, k dřívější obdobné informaci v našem magazínu uvedené.

Zde uváděná informace zpřesňuje a doplňuje podmínky platnosti uváděných vztahů pro rychlosti stoupání v motorovém letu.

Tak je možné při znalostech výkonu pohonné jednotky, její účinnosti (včetně účinnosti vrtule), rychlosti klesání příslušející letovým podmínkám klouzavého letu a hmotnosti stroje stanovit celkem obstojně rychlost stoupání při zvolených rychlostech letu.

Druhý z uvedených vztahů má širší platnost než ten první.

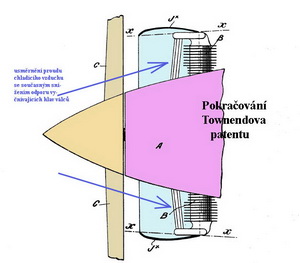
T

Townendův prstenec ( AL 1/09 – Ohlédnutí do minulosti – 5.část)

Hvězdicové motory vrtulových pohonných jednotek, dříve hojně používané, byly zdrojem zvýšeného odporu létajících strojů. Jednak měly válce, obvykle jich bylo kolem devíti a více, umístěné na poměrně velkém průměru a jednak je bylo třeba dobře chladit, takže je nebylo možno příliš ukrývat v obrysech trupů.

Výsledkem mnohého „přemýšlování“ ve třicátých letech 20. století pak byl návrh upravit kryt motoru tak, aby byl snížen odpor a zajištěno dostatečné chlazení.

A tak spatřil světlo světa návrh Angličana, jménem Hubert Charles Henry Townend, který byl patentován například v Kanadě 14.10.1930. Jedno ze schémat patentové přihlášky je na připojeném obrázku. Je doprovázen obrázkem s jednou z aplikací na francouzském turistickém hornoplošníku „Phrygane“ z roku 1935.

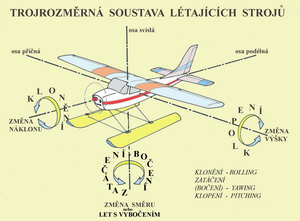
O nějakou dobu později byl v USA v National Advisory Comitee for Aeronautics navržen obdobný kryt s prodlouženou hloubkou stěny – „N.A.C.A. cowling“, který se pak také hojně používal.

Trojrozměrná soustava létajících strojů

Trojrozměrná soustava sestávající ze tří os s počátkem umístěným v těžišti letounu(modelu), umožňuje určení na něj působících sil a momentů.

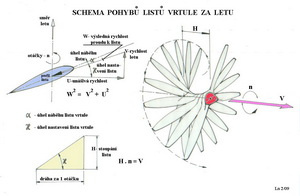
Vyjádření sil a momentů v aerodynamické souřadnicové soustavě, včetně používaného názvosloví je uvedeno v následující tabulce:

Osa podélná

odpor X(Q), součinitel odporu cx ,

X=c_x . ρ/2 . V² . S

charakteristický rozměr – velikost nosné plochy…..S

klonivý moment , součinitel klonivého momentu mx , M_x=m_x . ρ/2 . V² . S . l

charakteristický rozměr – rozpětí nosné plochy …. l

Osa svislá

vztlak Y , součinitel vztlaku cy , Y= c_y . ρ/2 . V² . S

zatáčivý moment , součinitel zatáčivého momentu my , M_y= m_y . ρ/2 . V² . S . l

charakteristický rozměr - rozpětí nosné plochy…..l

Osa příčná

příčná síla Z , součinitel příčné síly cz , Z=c_z . ρ/2 . V² . S

klopivý moment , součinitel klopivého momentu mz , M_z=m_z . ρ/2 . V² . S . bAS

charakteristický rozměr-střední aerodynam. tětiva…..b_AS.

Všimněte si, že ve všech vzorcích je zastoupen dynamický tlak ρ/2.V² proudu vzduchu nabíhajícího na nosnou plochu, jinak řečeno je to při rychlosti letu V.

V

Vrtule

Jestliže chceme k pohonu létajících strojů využít principu akce a reakce, kdy je pohonnou jednotkou uváděno do pohybu značné množství hmoty ne příliš velkou rychlostí(vztaženo například k výstupním rychlostem z trysek reaktivních motorů) dozadu za letadlo, tak využijeme schopností, kterou poskytuje vrtule.

Jak asi pracuje takový element letadla je uvedeno schematicky v následujícím obrázku, kde je zachycen šroubový pohyb vrtule, protože ten při pohonu a za letu každá její část, mimo osy, vykonává.

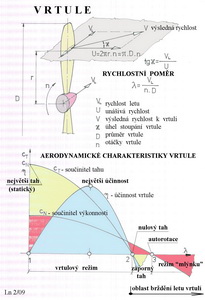
Vpravo nahoře je graficky znázorněna závislost mezi stoupáním vrtule a jejím rotačním pohybem. Stoupání vrtule - H udává dráhu jakou může vrtule urazit za jednu otáčku.

Vlevo nahoře je uveden trojúhelník vektorů rychlostí s nimiž se vrtule během letu potýká. Mezi tětivami profilů listu a vektorem výsledné rychlosti, zde označené W, jakou se pohybují ve vzduchu po šroubovici, je třeba zachovat vhodný úhel náběhu, při němž budou aerodynamické výkony profilu nejlépe využity.

Vlevo dole je uvedena grafická a početní závislost mezi rychlostí letu V a stoupáním vrtule H během otáček n v průběhu jedné sekundy.

A pak je tu další obrázek s obdobným znázorněním funkce vrtule jako obrázek předchozí, pouze s trochu jiným označením.

Na každý element vrtule „dotírá“ jiná rychlost obtékajícího vzduchu, zde označená V. Tato rychlost je geometrickým součtem rychlosti letu V_L a rychlosti unášivé(rotace) U. Výsledná rychlost svírá s rovinou rotace úhel κ (kapa).

Jestliže uvedeme rotující vrtuli do pohybu můžeme s výhodou popisu jejich vlastností použít poměru rychlosti dopředného pohybu(letu) V_L a součinu otáček a průměru vrtule(ve jmenovateli). Tomuto výrazu se říká rychlostní poměr. Pomocí něho lze popsat pohyb vrtule ve vzduchu.

U vrtule nás zajímá především velikost tahu, který je schopna vyvinout a výkon, který je schopna přenést z motoru na letoun. Obě tyto veličiny vztaženy pomocí součinitele tahu c_T a součinitele výkonnosti c_N ku rychlostnímu poměru λ mají pak stejnou funkci jakou součinitele vztlaku a odporu v závislosti na úhlu náběhu(což již známe).

A teď ke spodní části obrázku. Zde jsou na svislou osu vynášeny součinitele tahu a výkonnosti společně s účinností vrtule. Na ose vodorovné je průběh rychlostního poměru.

V bodě 1 stojí otáčející se vrtule na místě a má největší tah, protože zkroucený list vrtule je ofukován po celé své délce(poloměru) pod velkými úhly náběhu. Pokud jsou takto posuzovány vrtule s většími hodnotami stoupání pak se setkáme s velkým spotřebovávaným výkonem motoru a také často s velkým hlukem způsobeným odtrháváním proudu od listů. Účinnost je rovna nule, přes značný příkon, protože vrtule stojí na místě a nekoná proto svým tahem užitečnou práci. V podstatě pouze rozhání vzduch.

Jestliže se letoun dá s rotující vrtulí do pohybu dostáváme se do tzv. vrtulového režimu, kdy účinnost celého procesu nejprve rychle stoupá, aby po dosažení svého maxima začala zase klesat. Když stále zvyšujeme rychlostní poměr λ, k tomu dochází např.při stejných anebo menších otáčkách a snahou o zvýšení rychlosti letu, využitelný tah vrtule se zcela vytratí stejně tak jako účinnost. Pro to, aby se vrtule mohla stále otáčet i v tomto režimu potřebuje nezbytnou výkonnost pro překonání aerodynamických odporů. Je to bod 2 v diagramu.

Naší snahou je proto vždy zvolit pro svůj létající stroj takový rychlostní poměr, aby účinnost vrtule byla co největší. S tím bezprostředně souvisí i volby průměru a úhlů nastavení listů. To je dost komplikovaná záležitost, kterou teď nebudeme vysvětlovat.

Při dalším zvětšování λ se dostáváme s vrtulí do režimu brzdění. Vrtule mezi body 2 a 3 vyvozuje záporný tah(proti směru letu a tedy se sčítá s celkovým odporem), i když stále ještě nějakou výkonnost spotřebovává.

Jakoukoliv výkonnost přestane vrtule potřebovat dostane-li se do režimu autorotace, je to bod 3, kdy se samovolně otáčí(pokud jí v tom nebrání nějaké odpory). Takhle běžně pracují rotory vírníků a také rotory vrtulníků při sestupu bez motoru.

Dalším posunutím na ose rychlostního poměru vpravo se dostane vrtule do tzv. režimu „mlýnku“, kdy sice stále brzdí, ale je již schopna dodávat výkonnost. To je princip využívaný u větrných elektráren nebo pro znovu spuštění motoru letadla dynamickým účinkem vzduchu při zvýšené rychlosti klouzavého letu.

Vyvíječe vírů( Vortex Generators )

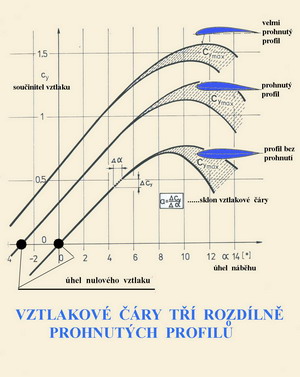
Plůtky ve formě tenkých a k povrchu ploch kolmo postavených plošek svírají se směrem proudu nabíhajícího k nim různé úhly náběhu. Jimi způsobené víry oživují proud mezi nimi přenášením energie proudu z vnějšku mezní vrstvy k povrchu obtékané plochy a tím uvádějí do pohybu na nich ulpívající částice proudu, jež jsou z hlediska proudění nežádoucí přítěží.

Takto povzbuzený proud má větší schopnosti neodtrhávat se tolik od obtékaných ploch s velkým zakřivením, což mohou být například místa u vztlakových klapek s větší výchylkou.

Odpor tak poněkud klesne a tak se může celková účinnost plochy zlepšit. Je možné to úspěšně aplikovat jak u nosných tak i ocasních ploch. Není však možné tím zcela odstranit nepříznivé účinky příčin, jež způsobily nežádoucí následky.

Vztlakové čáry profilů

„Posláním“ každého profilu nosné nebo ocasní plochy je vytvářet vztlak. Odpor při tom vznikající je obvykle nutným průvodním zlem.

Jednou z aerodynamických charakteristik profilu je průběh součinitele vztlaku na úhlech náběhu. Vztlak je hlavně ovlivněn prohnutím profilu a rozložením tloušťky po jeho hloubce.

Při dostatečně rozvinutém proudění kolem profilu má vztlaková čára, ve své převážné části, tvar přímky. Ve své horní části je vždy zakřivena u vyšších úhlů náběhu směrem doprava(k větším součinitelům odporu), dosahuje svého maxima a po jeho překročení klesá dolů. Odpor při tom stále narůstá. Jestliže je průběh její horní části plochý, tj. s malým zakřivením, jedná se obvykle o nezáludný profil u něhož dochází k odtrhávání proudu postupně od odtokové hrany kupředu. Jestliže má však její horní část zakřivení velké, s prudkým poklesem hodnot součinitele vztlaku, nelze očekávat pohodu při létání s velkými úhly náběhu.

Na připojeném obrázku jsou tři příklady vztlakových čar různě prohnutých profilů zachyceny.

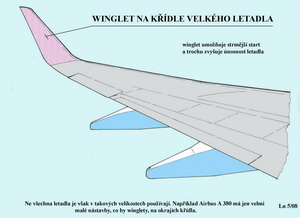
W

Winglety

Nejprve připomeneme anglický výraz, kterým je „washout“. To je případ kdy se snažíme upravit tvary a tím i vlastnosti křídla jestliže opatrně a rozvážně působíme na rozložení vztlaku podél jeho rozpětí. Vztlak je obvykle největší uprostřed křídla a směrem ke koncům klesá až na nulu. Zde, bez dalšího vysvětlování, upozorníme na metodu Multhopovu, Schrenkovu či Prandtlovu, které nezbytně provázejí designéry nosných ploch již po mnoho desetiletí. Jedná se mimo jiné o to, aby nedocházelo k prvotnímu odtrhávání proudu vzduchu od křídla v oblasti křidélek. To je velmi nežádoucí. Zmíněné metody spojené s úpravami tvarů křídel tomu pomáhají zabránit. Celkový dosažitelný vztlak křídla však poněkud klesne.

Winglety, což jsou nástavby pevných křídel letadel, mají právě opačnou úlohu než „washout“, podporují efektivnější využití vztlaku vyvozovaného na koncích křídla. Používá se pro to i výraz „aerodynamic wash-in“. Winglety by tedy měly působit podobně příznivě jako zvýšení štíhlosti křídla, aniž by se muselo zvětšovat jeho rozpětí. Tím zlepšují využití vztlaku na okrajích křídel a také zmenšují indukovaný odpor způsobený okrajovými víry křídla.

To znamená, že se příznivě uplatní při letech s většími úhly náběhu. Při létání s menšími součiniteli vztlaku, tj. při přeskocích kluzáků z jednoho místa na druhé, ač se u některých větroňů používají, mohou být při nesprávném návrhu spíše brzdou. Zejména v případech nevhodně volených a vůči okrajovým vírům nesprávně nastavených profilů.

Winglety však také tím, že „zachraňují“ část vztlaku u konců křídel, vytvářejí větší kroutící moment na křídle a to vede přes jeho nutné zpevnění v kroucení k jeho vyšším hmotnostem. Mohou také vyvolat zvýšený požadavek na washout kvůli citlivosti na spirální nestabilitu a tím i ke zhoršení optimálního rozložení vztlaku u daného tvaru křídla.

Jako jeden z prvních použil winglety Rutan na své „Vari Eze“ v roce 1975.

Na následujícím obrázku je ukázka wingletu na křídle velkého dopravního letadla.

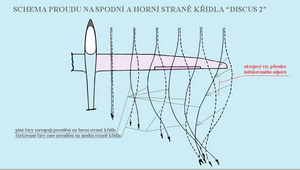
Další obrázek přibližuje schema proudění na spodní a horní straně jedné poloviny křídla . Zaznamenejte jak je obrazec proudění na horní straně „vyboulen“ směrem ke středu křídla a proudění na spodní straně zase k jeho okrajům. Tomu mají částečně zabránit winglety a pomoci tak snížit celkový odpor křídla při částečném zisku vztlaku.

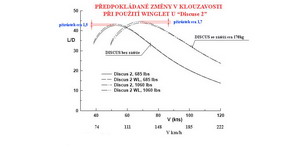
A na dalším obrázku je diagram předpokládaných průběhů klouzavostí u větroně Discus 2 , jednou se zatížením nosné plochy a podruhé bez něj, jestliže jsou či nejsou použity winglety. Jaké, to se neuvádí. Z diagramu je patrno, že přírůstky klouzavostí nejsou závratné i když jsou nějaké očekávány.

Od čeho je odvozeno slovo winglet přesně nevíme.

Mohlo by to však být spojeno s tím, že Angličan Fr.W.Lanchester v roce 1897 patentoval, kvůli ovlivnění vírů vznikajících na koncích křídel konečných rozpětí, „wing-end-plates“. Z toho mohl název winglet vzniknout. Je to však pouze naše domněnka.