Podobnost v aerodynamice
není čistě náhodná, jak se uvádí v mnoha jiných případech, aby nedošlo ke kolizi s právem, ale zcela adresná a neopomenutelná

V tomto pojednání nemáme na mysli podobu někoho s někým nebo připodobnění nějaké příhody s jinou, ale podobnost mezi ději jež probíhají při proudění tekutin a pro nás zvláště ve vzduchu. V mechanice tekutin jež mají reálné fyzikální vlastnosti – měrnou hmotnost, viskozitu a jež pro rychlosti plynů do asi 100 m/s pokládáme za nestlačitelné, působí ještě další stavové veličiny jimiž jsou teplota a tlak. Tyto veličiny obvykle působí společně a navíc se v průběhu času mění. Vzniká tak nekonečné množství variant dějů, které bychom, alespoň čas od času, chtěli nějak porovnat a pochopit.

Když se k tomu ještě připojí vliv geometrických tvarů a velikostí těles pohybujících se v prostředích tekutin nějakými rychlostmi je o neuspořádanosti z toho získávaných údajů postaráno. A to se nám nejen nelíbí, ale ani nehodí. A jak z toho tedy ven???

Je dost dobře nemožné sledovat při každém řešení létajících strojů působení prve uvedených okolností do nejmenších podrobností. Mnohem vhodnější je pokusit se získané poznatky zobecnit, případně se pokusit o jejich převod(přepočet) do jiných podmínek. Tak je možné například určit aerodynamické charakteristiky profilů ( součinitelé odporu, vztlaku a momentu) a nebo letové vlastnosti letadel z měření na jejich zmenšených modelech.

Jestliže však nevymezíme zcela jednoznačně způsob pro převod někde a nějak získaných údajů na podmínky jiné nejen, že se nedobereme chtěného výsledku, ale snadno dojdeme na scestí, jehož úskalí mnohdy ani nepoznáme. Taková činnost je pak zbytečná a zavádějící.

Co tedy chceme? Chceme mít možnost sledovat dva fyzikální děje takových za podmínek, abychom je mohli prohlásit za podobné. A co k tomu potřebujeme?

Jestliže budeme chtít prohlásit dva sledované jevy za podobné musíme pro ně zaručit :
    geometrickou (tvarovou) podobnost
    kinematickou (pohybovou) podobnost
    dynamickou ( silovou) podobnost.

Úplné dodržení všech prve uvedených podmínek není mnohdy možné, takže se musíme vzdát přání dodržet úplnou podobnost sledovaných dějů a musíme se spokojit s jejich částečnou podobností, která však musí obsahovat všechny vlivy na uvedené děje působící rozhodujícím způsobem.

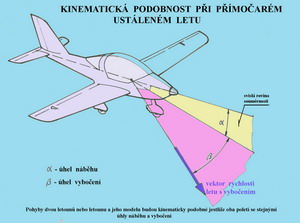
Na připojeném prvním obrázku je uveden příklad geometrické podobnosti dvou těles, v našem případě létajících strojů. Modelu označeného číslem 2 a jeho skutečného vzoru označeného číslem 1. Jsou-li oba stroje geometricky podobné, což znamená, že všechny jejich rozměry jsou ve stejném poměru změněny, pak stačí udat jeden, tzv. charakteristický rozměr. Obvykle volíme takový, který souvisí s nejdůležitějšími vlastnostmi tělesa.

U profilů je to jejich hloubka, u křídel jejich rozpětí a pro vrtule či rotory jsou to jejich průměry apod. Protože při proudění tekutin jsou velmi často výsledné účinky ( nás zajímají hlavně :vztlak, odpor, moment,..) odvislé od vznikajících sil a momentů, jež působí na nějakých plochách, je vhodné používat místo délkového rozměru charakteristickou plochu. Například půdorysnou plochu křídla a to i tu, která prochází trupem, příčný průřez pro trup a motorové gondoly apod.

Jestliže chceme posuzovat charakter proudění, který je podstatně závislý na vzájemném pohybu těles a proudícím prostředí (nebo prostředí nabíhajícím na ně, abychom využili principu relativnosti ), pak je nutné zaručit vedle podobnosti geometrické i podobnost pohybů (jejich kinematiky). Dva jevy mohou být podobné jedině tehdy jestliže vektory rychlostí budou mít v geometricky odpovídajících místech stejný směr. Obě tělesa se při tom mohou pohybovat různými rychlostmi. Nemůžeme však posuzovat případ kdy se jedno těleso otáčí a druhé vykonává pouze pohyb posuvný, bez otáčení.

Nejjednodušším případem pro nás bude rovnoměrný přímočarý pohyb letounu v klidném prostředí. Pro určení takového pohybu stačí udat polohu vektoru rychlosti s ohledem na něj. Tak jak je to uvedeno schematicky v dalším obrázku.

U vrtulí, například, je posouzení kinematické podobnosti poněkud složitější, protože se jedná o pohyb složený z pohybu rotačního a posuvného.

A nyní podobnost dynamická. Aby byly dva jevy dynamicky podobné musí být v obou případech u geometricky si podobných míst všechny zde působící síly podobné. Jedná se často o současné působení tlakových a třecích sil, sil tíže a nějakých sil vnějších.

Můžeme posuzovat podobnosti:

• výsledných a tlakových sil
• výsledných a vnějších sil
• výsledných, tlakových a vnějších sil
• výsledných a gravitačních sil
• výsledných a třecích sil.

My se soustředíme na podobnost poslední a sice na vztah mezi výslednými a třecími silami. A tím je Reynoldsovo číslo, které jakožto bezrozměrný údaj popisuje současný vliv setrvačných a třecích sil při proudění a z toho plynoucí účinky na tělesa pohybující se v tekutinách. Nás zajímá vzduch a létající stroje v něm.

Trochu historie, kvůli připomenutí gigantů vědy jež stáli ve své době u zrodu nových poznání, zajisté neuškodí.

Když v roce 1827 Francouz Navier a po něm nezávisle Angličan Stokes popsali proudění nestlačitelné, ale viskozní Newtonovské tekutiny podali základ pro výpočet vhodných a případně nejvhodnějších tvarů těles v nich se nacházejících. Dnes je tato soustava rovnic již řešitelná velkými počítači, což dříve možné nebylo.

Newtonův zákon viskozity lze zapsat například takto: ( začíná trochu přituhovat, jak jsme slíbili)

τ = -η . d_u / d_x

Zde znamená :
τ ….. tečné napětí v tekutině
η ….. dynamickou viskozitu
d_u….. rychlost proudění
d_x….. souřadnici kolmou na směr proudění.

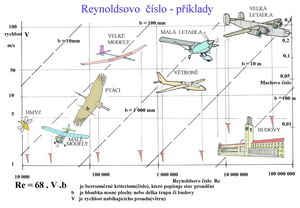
Američan Osborne Reynolds narozený v roce 1842 vytvořil v roce 1883 kriterium, které hodnotí podmínky nastávající při proudění různými rychlostmi, kolem různě velkých těles a za různé teploty a tlaku. Tím umožnil posuzovat okolnosti při nichž je možné zobecňovat výsledky dosažené při jednom ději na děj jiný. Jedinou, ale neopomenutelnou podmínkou je, aby jím vytvořené kriterium mělo v obou případech stejnou hodnotu. Jinak oba děje posuzovat zodpovědně nelze.

Toto jeho kriterium zvané Reynoldsovo číslo je jednou z nejdůležitějších pomůcek, ne-li nejdůležitější, při určování výsledků proudění tekutin na v nich ponořená tělesa. Je společně s dalšími bezrozměrnými čísly například Nusseltovým, Grashofovým, Froudeovým a Prandtlovým tak důležité, že se bez nich výpočty při jakýchkoliv prouděních a při přenosech tepla konvekcí nemohou uskutečnit.

Re číslo vyjadřuje svoji hodnotou stav „utkání“ mezi setrvačnými a třecími silami proudění, které spolu neustále soupeří. Převažují-li vlivy setrvačných sil Re číslo vzrůstá a podmínky dobrého obtékání těles se zvětšují- vztlak mírně vzrůstá a odpor zpočátku velmi rychle klesá. To je pro nás velmi příznivé.

Jestliže však převažují účinky třecích sil, jejichž příčinou jsou viskozity tekutin, pro nás to je vzduch, Re číslo klesá a podmínky obtékání se zhoršují - odpor vzrůstá a vztlak klesá. To si nepřejeme vůbec. Za to ale Re číslo nemůže, pouze nás na to upozorňuje a nabádá k tomu, abychom s tím něco udělali nebo se s tím smířili.

Nebo ještě jinak řečeno: Reynoldsovo číslo je vhodným parametrem pro posuzování stavu proudění. Vznik turbulentního (vířivého) proudění je způsoben porušením rovnováhy mezi silami tření uvnitř tekutiny, které se obecně snaží stabilizovat proud do spořádaných vrstev – laminárního (vrstevnatého) proudění a setrvačnými silami proudu. Od určitého poměru mezi nimi, kdy setrvačné síly začnou být rovnocenné silám třecím, dávají možnost vzniku tzv. kritickému stavu, kdy se střídavě mění vrstevnaté proudění ve vířivé. To jsou typické příklady mnoha menších modelů letadel při nichž na nosných a stabilizačních plochách kolísají hodnoty vztlaku a odporu dramaticky.

Hodnoty kriteria takového proudění, zvaného kritické Reynoldsovo číslo, se pohybují pro všeliké profily v rozmezí 25 000 až 150 000. Menší hodnoty platí pro tenké a také ne příliš prohnuté profily. Větší hodnoty pak pro profily s tloušťkami nad asi 17%. Jak lze snadno a rychle spočítat velikost Reynoldsova čísla? To popisuje následující rovnice s níž by se měl každý, kdo chce trochu porozumět proudění kolem letadel, úspěšně vypořádat.

Re = 68 . b . V ( - )

V tomto vztahu jsou zastoupeny třecí síly vzduchu číselnou hodnotou 68, což je převrácená hodnota kinematické vazkosti vzduchu pro teplotu cca 15^o C.

V zimě, kolem asi -10^o C je její hodnota cca 80 – viskozita plynů s klesající teplotou klesá a proto všechny létající stroje v zimě vykazují lepší výkony než v létě, jak si jistě alespoň někteří z čtenářů všimli. Naproti tomu v létě při teplotách kolem cca 35^o C. viskozita plynů stoupá (na rozdíl od kapalin) a do Re čísla můžeme dosadit číselnou hodnotu pouze do cca 60. Re číslo je tedy menší než v zimě a to o cca 25%, což je skutečnost již nezanedbatelná. S potížemi při létání se proto setkávají i větší letadla jestliže létají za těchto teplot. U modelů letadel je tato zhoršená skutečnost evidentní i pro málo zkušené modeláře na první pohled, i když si mnozí myslí jaké je to skvělé počasí pro let. Jaká šalba neinformované mysli! Teď již to však víte a proto buďte za horka obezřetní nejen na sebe, ale také na svoje létající stroje.

Symbol b jakožto zástupce geometrické podobnosti představuje zde hloubku střední aerodynamické tětivy nosné plochy létajícího stroje a dosazuje se v mm.

Symbol V zastupuje kinematickou podobnost děje a zde je to rychlost letu. Dosazuje se do tohoto vzorce v m/s. Jakých asi hodnot mohou v našem „hobby“ Reynoldsova čísla dosahovat? Na dalším obrázku je to stručně graficky uvedeno.

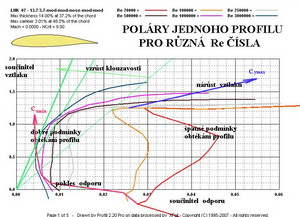
Pomohu trochu s pochopením.

Na vodorovné ose jsou hodnoty Re čísel pro obrázky zastoupené příklady nad nimi a to při teplotě kolem 150C. Začínáme vlevo dole s hmyzem a končíme vpravo velkými letadly a budovami. Na svislé ose souřadného systému vlevo je vynášena rychlost letu v v m/s. Šikmé čárkované čáry zastupují charakteristický rozměr, kterým je zde hloubka křídel b udávaná v mm a m. Vpravo na svislé ose jsou orientační hodnoty Machova čísla, které udává poměr rychlosti letu ku rychlosti zvuku za daných podmínek tlaku a teploty.

Z diagramu vidíte, že hmyzí nosné pohyblivé plochy dosahují obvykle průměrných hodnot Re čísel kolem 10 000 až 20 000.

Ptáci jsou již na tom lépe a jejich Re čísla mohou přesáhnout značně hodnotu 100 000, což je pro jejich tenké, i když dost prohnuté, profily již výhodné. . Ptáci se ale i s takovouto nevelkou přízní povětří, na rozdíl od nás, dokáží dost dobře vyrovnat Nemluvě o jiných příznivých účincích různých „fines“ s kostmi a peřím, jež jsme ještě asi úplně nepochopili

Naproti tomu u malých modelů letadel dosahujících na svých nosných plochách nepříliš vysokých Re čísel se to nezřídka projevuje na jejich nepřesvědčivých výkonech i vlastnostech. Bráníme se tomu tím, že volíme tenčí profily, asi tak do 9% maximální tloušťky, pro něž nejsou tak nízké hodnoty Re čísel ( 50 000 až 85 000) ještě úplně zničující. Velké modely a zejména rychle létající modely(někdy i přes 100m/s) mají Re čísla několik set tisíc, což již signalizuje, že podmínky obtékání mohou být dost příznivé. Větroně a malá letadla mají již díky svým rozměrům a zatížením nosných ploch Re čísla již přijatelná, dokonce dobrá. Proudění je kolem jejich ploch při Re číslech větších než cca 1 000 000 již vyvinuté natolik, že poměr vztlaku ku odporu je obvykle výborný.

Velká letadla mají u svých ploch Re čísla vyšší než cca 7 000 000 a to je činí méně choulostivými k nepříznivým účinkům třecích sil, pokud ovšem jejich povrchy nejsou nepřiměřeně hrubé, s mnoha výčnělky a nerovnostmi. To však platí ale i pro menší létající stroje, kde hrubé a nerovné povrchy se spoustou výčnělků jsou zdrojem zbytečných přídavných odporů.

Aerodynamika velkých budov, jejichž jeden náčrt je pro informaci vpravo dole, je samostatnou kapitolou pro stavaře a my se jí zde nebudeme zabývat, protože budeme mít dost starostí s svými pohybujícími se stroji.

S čím se ale tady velmi často budeme zabývat je vliv velikostí Reynoldsových čísel na aerodynamické charakteristiky profilů, kterými osazujeme nosné plochy. Na dalším obrázku je takováto skutečnost připomenuta zobrazením několika polár profilu s maximální tloušťkou 13,7% a prohnutím 3%, při různých Re číslech.

Součinitelé vztlaku a odporu vynášené na vodorovnou a svislou osu souřadného systému jsou zde zastoupeny šesti křivkami roztodivných tvarů.

Pro nejnižší Re = 70 000 je křivka úplně vpravo nepěkně deformovaná ve střední části směrem k velkým součinitelům odporu. To svědčí o velmi nedokonalém obtékání profilu i když součinitel vztlaku není zase tak nejhorší.

Druhá křivka-polára má již lepší tvar. Její celá střední část se posunula výrazně směrem k menším součinitelům odporu a vztlak mírně vzrostl. To svědčí o tom, že při tomto Re=100 000, se obtékání profilu velmi zlepšilo i když není ještě nijak výtečné. Profil se nachází za kritickou oblastí obtékání, kdy mají ještě značný nepříznivý účinek třecí síly.

Pro Re=250 000 jsou již aerodynamické charakteristiky podstatně lepší. Odpor znovu významně klesl na méně než polovinu předchozí hodnoty v rozmezí součinitelů vztlaku 0,1 až 0,9. Setrvačné síly již značně eliminovaly nepříznivé účinky viskozity vzduchu, po případě malé rychlosti letu.

Při Re=500 000 je již součinitel odporu menší než 0,01 pro poměrně široké rozmezí součinitelů vztlaku. Podívejte se také jak zde vzrostla maximální klouzavost profilu, což je nejlepší poměr součinitele vztlaku ku součiniteli odporu. Je to ta zelená plná čára vedená ke křivce z počátku souřadnic. Klouzavost profilu je teď 2:0,0178= 112, když pro Re=100 000 byla 2:0,0355=56,3, tj. nyní je dvojnásobná.

Při Re=1 000 000 dosahuje součinitel vztlaku hodnoty blízko 1,5 a nejmenší součinitel odporu je v poměrně širokém rozmezí úhlů náběhů kolem 0,006. To již stojí za povšimnutí.

A nakonec pro Re=3 000 000, což by mohly být například podmínky při rychlejším letu větroně, je minimální součinitel odporu kolem 0,0044 při nárůstu maximálně dosažitelného součinitele vztlaku až k 1,65. Maximální klouzavost profilu je nyní 2:0,0128= 156, o 28% lepší než u půlmilionového Re čísla.

Jestliže bychom uvažovali o použití tohoto profilu, jímž byl hypoteticky opatřen skutečný větroň, na model jehož Re číslo by bylo kolem 100 000, pak musíme počítat s tím, že jeho maximální klouzavost bude přinejmenším 156:56,3 = 2,77krát horší. A to nám napovědělo Reynoldsovo číslo.

Z toho plyne následující nápověda: nesnažte se „roubovat“ stejné profily jaké mají skutečné vzory na vaše modely v naději, že to bude skvělý počin. Počin to bude, ale s opačným účinkem a značným zklamáním.

Pro stavitele skutečných letadel si netroufám podat jakoukoliv nápovědu, protože jejich profesionální přístup jim jistě nezabrání neposoudit vliv Reynoldsova čísla na výkony a vlastnosti jejich výtvoru.

Co ještě dodat? Asi již nic, protože k Reynoldsovu číslu se budeme ještě vracet vícekrát.

Takže pouze připomínám, že zde probírané bezrozměrné kriterium stvořené panem O.Reynoldsem před cca 125 lety je veledůležitým vodítkem pro letecké modeláře a velmi důležitým ukazatelem i pro stavitele skutečných letadel při jejich cestě za pronikáním do atmosféry Země pomocí svých létajících strojů. Snažte se mu porozumět co nejlépe.

P.S.: Ještě několik, snad zajímavých, informací o tom jakých hodnot je dosahováno při různých, i když dost těžko srovnatelných dějích a to ne jenom ve vzduchu. Z webových stránek Wikipedie jsem vybral:

	Reynoldsovo číslo
pohybující se spermie (jsou to již ty líné nositelky rozmnožování, jimiž jsou údajně „vybaveny“ současné mužské generace jejich původců?)	0,01
krev v mozku	100
krev v aortě	1 000
rychle rozehraný míč v basketbalu	250 000
plovoucí člověk	4 000 000
plejtvák obrovský	300 000 000
zámořská loď	5 000 000 000

Prameny
Bauer, Brůha, Jaňour – Základy proudění, 1950
Internetové stránky Wikipedie
Vlastní archiv