Profily nosných a ocasních ploch, listů vrtulí a rotorů
1. část

Co je to profil?

Profil je uzavřená rovinná křivka vzniklá řezem nosné či ocasní plochy a také listem vrtule nebo rotoru (a rovněž lopatkou rotačního stroje) v rovině kolmé na jejich podélnou osu.

Navrhnout vhodný tvar profilu znamená vytvořit takovou uzavřenou křivku, která by mohla pomoci tvarovat povrchy křídla k dosažení požadovaných aerodynamických výkonů a vlastností. Největší důležitost je při tom kladena na dosažení co největšího poměru vztlaku ku odporu - to je tzv. aerodynamická jemnost profilu. Za velmi dobré profily jsou považovány ty, jejichž hodnoty aerodynamických jemností jsou nad hodnotou 150. Pak následuje požadavek dosahování co nejvyššího vztlaku s vhodnými průběhy momentů.

V průběhu cca 100 let byly zaváděny mnohé metody navrhování profilů. Například metoda singularit obcházející potíže se snahami rozšířit původní teorie profilů stavěné na konformních transformacích( např. Rus Žukovskij).

Tyto obsáhlé práce, zaměstnávající tisíce lidí v aerodynamických laboratořích na celém světě, byly postupně doplňovány metodami experimentálního a teoretického zkoumání vlastností mezné vrstvy, kde se projevují hlavně účinky třecích sil a vytvořily současný základ navrhování profilů pro jejich rozsáhlé používání v letectví a strojního inženýrství točivých strojů(ventilátory, dmychadla, turbiny, kompresory atd).

Mnozí konstruktéři letadel se snažili využít poznatků z ptačích křídel. Kopírovali proto jejich tvary i tvary profilů. Bylo to určitě podnětné, i když se tvary křídel mrtvých ptáků i jejich profilů lišily od stavu, kterým disponovali ptáci živí. Ještě ve dvacátých letech dvacátého století byla křídla ptáků a způsoby jejich létání předmětem zájmu mnoha jedinců. O tom, zda byly využity již všechny informace ze světa ptáků a hmyzu, je ale i dnes těžké rozhodnout.

Ohlédneme-li se dále do minulosti letectví můžeme zjistit, že osudy profilů letadel těžších vzduchu se ubíraly klikatými cestami.

Počátkem 16. století Leonardo da Vinci poznal, že pro let není nutný jen mávavý pohyb křídel podle vzoru ptáků a hmyzu. Pochopil, že křídlo může být nehybné vůči ostatním částem létajícího stroje a opatřené profilem s vhodným tvarem a přiměřenou tloušťkou. Zabýval se i myšlenkou rotujících křídel. Pak se jeho poznatky zachycené v jeho poznámkových „kodexech“ někam vytratily a byly po několik set let znepřístupněny.

Na počátku 19. století to byl Angličan George Cayley, který vyzbrojen poznatky Newtonovými, Eulerovými i svými vlastními navrhoval a také při svých experimentech používal, celkem úspěšně, profil vhodné tloušťky a prohnutí. To byl podnět, který ale byl, dost nepochopitelně, následujícími pionýry letectví v tom století nevyužit.

Teprve na konci 19.století Němec Otto Lilienthal obrátil pozornost všech, kdo chtěli naslouchat, správným směrem, i když jeho profily byly tenké a s nemalým prohnutím.

Cayleyho „nápovědu“ týkající se profilů nosných ploch nevyužil nikdo před koncem 19. století. To znamenalo zmaření mnoha nákladných pokusů s létajícími stroji v té době, přestože někteří byli již dost blízko.

Nejpoužívanějším tvarem profilu křídel byla rovná deska, viz následující obrázek, která však neumožňovala svými vlastnostmi dosahovat potřebného vztlaku a také zajistit dostatečnou provozní pevnost, takže vyztužení takových obrovských křídel připomínalo plachtoví se stožáry u lodí. Odpor těchto nosných ploch byl značný. Ne příliš šťastný vliv zde měl i Newtonův vzorec pro výpočet aerodynamické síly v němž byl zakotven i sinus úhlu náběhu desky. Ten posouval skutečně dosažitelný vztlak do velmi malých hodnot a proto měla křídla tehdejší doby s profily ve tvaru rovných desek zbytečně obrovské plochy.

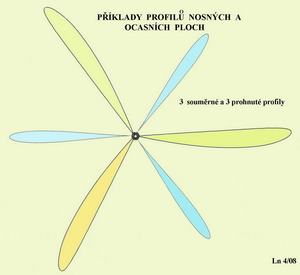
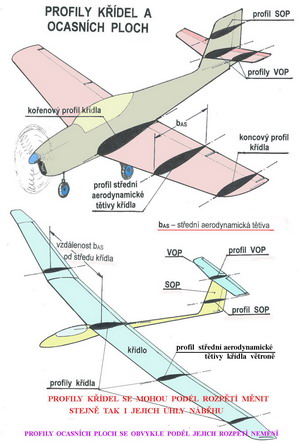
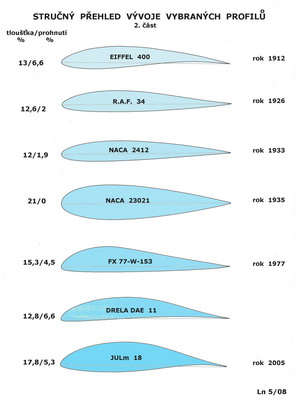
K letům nepomohly těmto strojům ani některé skvělé konstrukce parních strojů, které v té době byly jedinou možností sestrojit vrtulovou pohonnou jednotku. Profily listů vrtulí měly, jak jinak, také tvar rovných desek a u některých nebyla ani dodržena zásada potřebného zkroucení listů podél průměru. Účinnost těchto pohonných jednotek nemohla být jiná než bídná a proto pro lety nedostatečná.

V roce 1871 však Francouz Alphonse Pénaud předvedl úspěšný let svého modelu s tlačnou vrtulovou pohonnou jednotkou členům Francouzské akademie. V křídle i vodorovné ocasní ploše měl tenký prohnutý profil. Model proletěl, poháněn energií gumového svazku, vzdálenost několika desítek metrů. Zdálo by se tedy, že důkazů o možnostech uskutečnit let s pevnými křídly je již dost, ale trvalo to ještě více než dvacet let než O.Lilienthal to na svých závěsných kluzácích dokázal a prokázal.

Na následujícím obrázku je příklad toho jaké profily mohou být obsaženy v nosných a ocasních plochách létajících strojů.

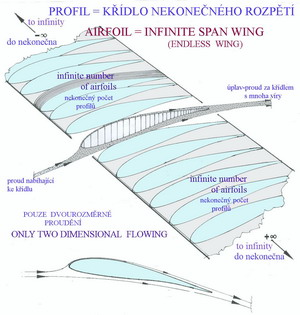
Protože profil je pouze rovinným obrazcem nelze mu přiřazovat vlastnosti jimiž jsou vztlak, odpor, moment apod. Proto jej nahrazujeme při dalších úvahách pojmem křídla nekonečného rozpětí, u něhož již můžeme na důsledcích dvourozměrného obtékání kolem něj posuzovat jeho aerodynamické vlastnosti. Příklad křídla nekonečného rozpětí je na obrázku.

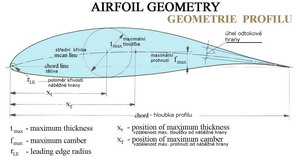
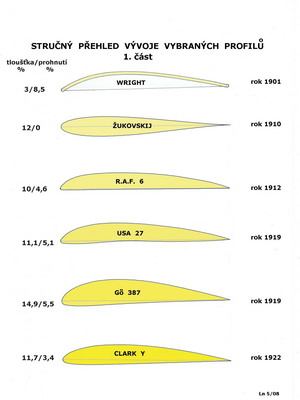
Abychom mohli porovnávat vlastnosti jednotlivých profilů je třeba je nějak geometricky popsat. Samotný tvar křivky nám nestačí. Proto je obrys profilu popsán vhodně zvoleným počtem souřadnic v pravoúhlém systému, které definují jeho tvar. V některých případech má souřadný systém počátek vlevo(na náběžné hraně) v jiných zase vpravo(na odtokové hraně). Na dalším obrázku je schéma profilu v souřadném systému s uvedením některých dalších geometrických charakteristik.

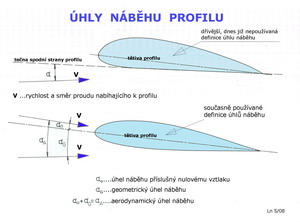
Na dalším obrázku jsou ještě jiné geometrické charakteristiky profilů zachyceny. Jsou to:

• Tětiva profilu, která spojuje náběžnou a odtokovou hranu křídla nekonečného rozpětí(profilu, jak jsme již vyjádřili dříve). Její délka - hloubka profilu je vztažnou hodnotou pro bezrozměrné profilové veličiny.
• Střední křivka je spojnicí středů kružnic vepsaných do obrysu profilu. Maximální vzdálenost mezi tětivou a střední křivkou představuje největší hodnotu prohnutí profilu. Je rovněž důležitá jeho vzdálenost od náběžné hrany.
• Rozdíly mezi souřadnicemi horní a spodní strany profilu udávají velikosti tlouštěk v těch místech. Největší tloušťka profilu je v místě vepsané kružnice s největším poloměrem. Vzdálenost maximální tloušťky profilu od náběžné hrany je rovněž důležitá.
• Poloměr náběžné hrany určuje zakřivení obrysu profilu v jejím bezprostředním okolí.
• Úhel odtokové hrany má být pro naše případy nízkých rychlostí vždy co nejmenší.

  Z uvedených geometrických charakteristik mají největší vliv na výkony a vlastnosti profilů velikosti a průběhy tlouštěk v závislosti na prohnutí.

  V předchozím obrázku jsou uvedeny zbývající základní geometrické charakteristiky profilu, které je vhodné pochopit a porozumět jim.

  Jednotlivá letadla určená k různým účelům využívají přirozeně i profilů s různými tvary a vlastnostmi. Jeden profil není schopen vyhovět úspěšně zcela rozdílným požadavkům létajících strojů. Na dalších dvou obrázcích je velmi stručně a nekompletně uveden pokus zachytit jakýsi vývoj profilů od počátku 20. století dodnes, pro oblast nižších rychlostí letu, dejme tomu do 450km/h.

  Jak již bylo naznačeno v předchozím textu ubíral se vývoj profilů různými cestami i cestičkami, což lze pozorovat občas dodnes. Zejména letečtí modeláři, ale i stavitelé malých skutečných letadel, aplikují při tom svoje poznatky a způsoby uvažování, která jen vzdáleně odpovídají věrohodným metodám navrhování profilů.

  Mnohé populární profily 20.let 20. století byly navrhovány intuitivní metodou „pokus-omyl“. Bez jakékoliv vazby na teorii či systematické experimentování. Nedá se říci, že jejich tvůrci byli ve své době vždy neúspěšní. To ale nepotvrzuje správnost jejich cesty. Například G. Loeving použil jako profilu křídla svého hydroavionu využívajícího na horní straně tvar z profilu R.A.F. 15 a pro spodní stranu souběžné podobné křivky s vyboulením v místě uložení nosníků křídla.

  V.Clark navrhl v roce 1922 jeden z legendárních profilů nosných ploch i vrtulí známý CLARK Y. Jednoduše využil tehdy známých výsledků světoznámé aerodynamické laboratoře v německém Gőttingen. U jednoho z jejich tlustších profilů pozměnil jejich průběh(profil ztenčil) a prohnutou spodní stranu nahradil z velké části přímkou. Učinil tak údajně proto, že tak obdržel spolehlivou referenční plochu pro jednoduché nastavení úhlů náběhu po délce listu při výrobě vrtulí, kde byl angažován.

  Letečtí teoretici brzy pochopili, že k širšímu úspěšnému použití profilů je třeba systematické analytické metody, včetně testů v aerodynamickém tunelu. Tak začal obrovský rozvoj experimentování v aerodynamických tunelech po celém světě, kde na to ovšem měli dost peněz. Organizace NACA se v USA začala s rozsáhlými pracemi již v roce 1920 a to po několik let pod vedením Němce M.Munka, žáka L.Prandtla z Gőttingen. Jeho metody a způsoby jednání se však mnohým podřízeným nelíbily a tak se potýkal s častým protivenstvím. V Anglii to byla například instituce British National Physical Laboratory. Nebo Eiffel ve Francii také konal nákladné pokusy v tunelu. Jeho systém otevřeného tunelu(vstup a výstup povětří do něj začínal a končil v okolním vzduchu) byl však poměrně rychle nahrazen uzavřenými okruhy, které umožňovaly dosahování vyšších rychlostí proudění při ještě přijatelných provozních nákladech na pohonná soustrojí. Proudění se však vyznačovala poměrně značnou turbulencí, což po dlouhou dobu zůstávalo nepovšimnuto, ač to společně se značným hlukem v tunelu nezanedbatelně ovlivňovalo výsledky testování. Pokud se jednalo o Reynoldsova čísla měření nad asi 2-3 miliony, tak se nad tím daly jakž takž přimhouřit obě oči. Po čase se však míra turbulence, úroveň hluku a nerovnoměrná oteplení úseků tunelu začaly pečlivěji sledovat a napravovat. Měly značný vliv na výsledky experimentů, které tak nenapomáhaly věrohodnostem teoretických návrhů profilů.

  Problematika aerodynamických tunelů, jejichž éra ještě neskončila, je velmi rozsáhlá. Sám jsem se o tom přesvědčil, když jsem asi před 28 lety provozoval svůj malý amatérský tunel s otevřeným okruhem a průměrem měřícího prostotu cca 600mm, kde jsem dosahoval maximální rychlosti proudění do 25m/s. Větší motor než 5KW jsem neměl. Ale i tak to dělalo hrozný hluk. O obtížnostech verifikování dosažených výsledků ani nemluvě.

  Raději tunely opustíme a vrátíme se zpátky k profilům, pro jejichž navrhování již dnes existují velmi dobré výpočetní programy. Z nich neznámější je „X-FOIL“ prof. Drely z amerického Massachuset Institut of Technology. Podle jeho programu je možné navrhovat všeliké profily a sledovat jejich výkonové charakteristiky. Tento program je volně přístupný na internetu. Z něj pak vyšli autoři jiných programů tím, že ho zjednodušili. Jedním z nejznámějších je italský program „PROFILI 2.20“ od St. Duranti. Ten je nejen v tomto článku využíván.

  Chování profilů závisí nejen na jejich tvaru, ale také, mimo jiné, na poloze vůči směru letu. Tato skutečnost je vyjadřována úhlem, který svírá tětiva profilu se směrem letu(nebo jinak řečeno se směrem proudu vzduchu k němu nabíhajícímu).

  V aerodynamické praxi se obvykle lze setkat se třemi pojmy úhlů náběhu:

  1. úhel náběhu při nulovém vztlaku profilu, který je pro prohnuté profily vždy záporný, ale pro souměrné profily je vždy roven nule
  2. úhel náběhu sevřený mezi tětivu profilu a směr letu, je to tzv. geometrický úhel náběhu. Ten může mít hodnoty kladné i záporné
  3. konečně je to aerodynamický úhel náběhu, který je součtem obou dvou předchozích hodnot.

  Všechny tyto úhly jsou na následujícím obrázku uvedeny. Je zde ještě připomínka dřívějšího způsobu vyjadřování úhlu náběhu profilu, který byl ale opuštěn kvůli nemožnosti jednotného posuzování různě tvarovaných profilů.

  Pak jsou to ještě jiné úhly související s polohou profilu nosné plochy vůči létajícímu stroji na němž je použit. Viz další obrázek.

  Jsou to následující pojmy, které by měly být používány s plnou zodpovědností k důležitostem, jaké zaujímají při návrhu letadla.

  • a)úhel nastavení je ten úhel, který svírá tětiva křídla s osou trupu
  • b)úhel seřízení je ten, který svírá tětiva křídla(křídel) s tětivou VOP
  • c)úhel postoje na Zemi je tím úhlem, který umožňuje využít co nejvyšší součinitele vztlaku při startu a přistání, aby k tomu potřebná dráha nebyla tak dlouhá a rychlosti, zejména při přistání, nepřiváděly posádku v úžas nad tím, co si s tím mají počít při tak velké rychlosti a rychle se přibližujícím konci dráhy.

  Na dalším obrázku je schéma obtékání profilu při různých úhlech náběhu. Zde jsou to geometrické úhly náběhu. Jsou zde rovněž zachyceny přibližné vektory místních rychlostí proudu V v bezprostřední vzdálenosti od povrchů profilu.

  Všimněte si jak se mění vírová stopa-úplav za profilem v souvislosti se změnami úhlů náběhu. Jedná se o mírně prohnutý profil, který již při nulovém náběhu vykazuje určitý vztlak(horní schéma). Odpor je také velmi malý, ale protože i vztlak není příliš velký je aerodynamická jemnost profilu dost malá.

  Druhé schéma představuje situaci při nějakém zvýšeném úhlu náběhu, kdy se zvýšil vztlak, ale i trochu odpor. Vztlak se však zvětšil poměrně víc, takže aerodynamická jemnost stoupla.

  Další schéma ukazuje situaci při letu se záporným úhlem náběhu. Vztlak se zmenšil dramaticky, ale odpor nijak zvlášť. U více prohnutých profilů jak uvidíme později, se dokonce velmi zvětšil. Aerodynamická jemnost nabývá záporných hodnot a letadla se v těchto polohách pohybují strmým letem k Zemi nebo letí „na zádech“.

  Spodní schéma zastupuje situaci při pokusu letět při velkém úhlu náběhu, k čemuž dochází obvykle při startu nebo přistání. Někdy také při špatně vedené zatáčce, což je velmi nebezpečné. Vztlak se již nejen nezvětšil, mnohdy už se zmenšuje, ale odpor narůstá dramaticky. Výsledná aerodynamická síla se sice také zvětšuje, ale současně mění rychlost letu. To vede často k nechtěnému pádu. Pokud není k dispozici rezerva ve výkonu pohonné jednotky, dostatečná výška a zkušený pilot, je na obrovské potíže „zaděláno“.

  Zvláštní situace nastávají například u křídel malých štíhlostí, kde okrajový vír příznivě ovlivňuje přiléhavost proudu po větší části rozpětí než u křídel štíhlejších, takže je možné při přistání letět i při větších úhlech náběhu než asi 15 stupňů.

  To byl úvod do občas tajemné říše proudění kolem profilů. Teď se ještě vrátíme k tomu jak to vypadá při obtékání některých těles , jejichž výsledky byly využity pro formulování mnoha základních poznatků využitých při navrhování profilů.

  Na dalším obrázku jsou příklady přibližných velikostí odporů při proudění kolem čtyřech těles.

  Srovnejte velikosti odporů ve všech pěti případech. Jedná se o nadkritické proudění, tj. při dostatečně velkých Reynoldsových číslech. Změny odporu jsou v těchto případech více než stonásobně odlišné.

  Jaroslav Lněnička

  1. 7. 2008