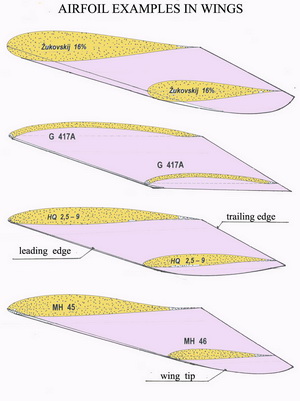
Profily nosných a ocasních ploch,listů vrtulí a rotorů
2.část

Hned v úvodu uvedeme jednu ilustraci související s možnými použitími profilů na létajících strojích. Jsou zde uvedeny čtyři příklady profilů, jak mohou být nalezeny v některých nosných nebo ocasních plochách.

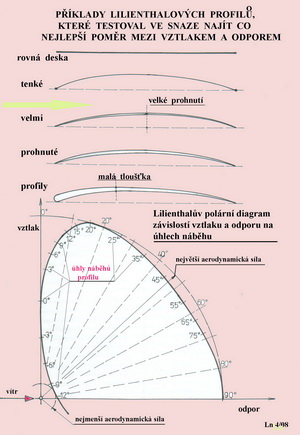
Teď bude zřejmě vhodné zabrousit do „nomenklatury“ proudění tekutin a v rámci našeho populárně naučného způsobu některé pojmy zatím odložit a jiné zase připomenout.

Takže ponecháme stranou například pojmy : rychlostní pole ; rotor rychlosti ; potenciální proudění ; potenciální pole, kdy je cirkulace rychlosti rovna nule ; vířivé pole, kdy zase cirkulace rychlosti podle nějaké uzavřené křivky(profilu) není rovna nule ; Stokesovu větu o vírovém toku ; vírovou trubici skládající se z vírových vláken ; metodu konformního zobrazování, u níž je daný geometrický tvar převáděn na tvar jiný pomocí funkce komplexní proměnné, jež je volena tak, aby se proudová pole v nekonečnu spojila, když se vychází zpravidla z obtékání kružnice přetvářené v úsečku, elipsu nebo profil, atd. A již uhýbám před hozenými kameny od aerodynamických bezvěrců a raději končím i s tím co vynecháváme.

Stranou ale neponecháme pojmy jako: rovnici Bernoulliho, kterou lze při zanedbání potenciálních výšek vyjádřit jako stálý součet statického a dynamického tlaku(+ ztráty) v proudící tekutině ; rovnici kontinuity – průtok tekutiny je spojitý a vyjadřující princip zachování energie ; proudové čáry – proudnice , jejichž síť vytváří proudnicový obraz rychlostního pole proudící tekutiny ; proudění laminární a turbulentní ; mezní vrstvu ; viskozitu tekutin ; Reynoldsovo číslo ; …

Protože bychom z populárně naučného způsobu vytvořili pouhé tlachání, jaké můžeme bohužel často zaslechnout mezi letectví zasaženým lidem, což nás, mimo jiné, přivedlo ke stvoření tohoto magazinu.

Povídejme o proudění vzduchu kolem profilů, zase trochu jinak aneb předčítejme z jedné části hrůzostrašného románu zvaného „Mechanika tekutin“.

Začněme obrázkem s příklady Lilienthalových profilů, které testoval ve snaze získat údaje o nosné síle a přetvořil je do diagramu v tzv. polárních souřadnicích, od té doby zvané po celém světě polára. Proč a jak bude sděleno později.

Co lze a co ne, říci o proudění kolem profilů ? Jak vystrašit příznivce létajících strojů, ať již vlastních nebo vypůjčených, aby jim byla věc létání věcí nejsvětější? Čím zajistit jejich nepravidelný spánek se spoustou příšerných snů a zpocenou kůží? Kterou myšlenkovou substancí vymýtit, aby již přestala kalit jejich mysl, křivila a zamlžovala jejich vztah k létání a letadlům? O jedné víme, působí spolehlivě. Zaryje se pod kůži a je většinou neodstranitelná. Dovolíme si na ni upozornit, ač je to okolnost notoricky známá a vznikla jistě již před tím, než byl sestrojen ten nejprvnější stroj určený k létání, ať již na pohyblivých nebo pevných křídlech.

Je to neviditelná podívaná na to, co se děje kolem těles kolem nichž proudí vzduch nebo těles pohybujících se vzduchem. Pro jednoduchost budeme uvažovat pouze vzduch nepohyblivý, tedy bezvětří. Připomeňme, že účinky klidného vzduchu na pohybující se těleso v něm jsou tytéž, jako ty, které vznikají na nepohyblivém tělese kolem něhož vzduch proudí. Je to tak zvaný princip relativnosti proudění, který je využíván v aerodynamických tunelech a který byl již dávno zaznamenán zájemci o lety například ptáků. Mezi ty, kteří tento vztah pochopili a správně interpretovali, patřil například Leonardo da Vinci, když spřádal svoje sny o létání na kopci a díval se na orly plachtící nad stejným místem dlouhé minuty, bez znatelného mávání křídly, pouze s nepravidelným nakrucováním konců křídel, v reakci na nestejnoměrný vítr porušující jejich rovnovážnou polohu. Zjistil, že vítr vyvolává zřejmě tytéž účinky na předmět v něm umístěný, jako když se ten pohybuje v klidném vzduchu. Nechal obživnout myšlenky a nápady, které nesporně inspirovaly ty, kteří se o nich dozvěděli později. Bylo jich ale málo, těch průkopníků letectví, jež se k nim dostali, protože jeho poznámky nebyly po více než tři století přístupné veřejnosti.

V tomto okamžiku můžeme tedy směle říci, že jsme zviditelnili jednoho z duchů používaných k zastrašování poznání chtivých příznivců létání, jenž vystupuje ve všech úvodech do vědy zvané aerodynamika. Vězte tedy, že princip relativnosti proudění je pouze jedním z prostředků umožňujících vysvětlení mnohých dějů z mechaniky tekutin. Nic víc v něm není třeba hledat.

Když na něco nevidíme, tak si na to posvítíme. Jak si posvítit na proudící vzduch? Trochu ho zviditelníme. Třeba tak, že do něho vpustíme drobné praménky barevného kouře, které dost věrně ukáží co se ve vzduchu děje. Zjistíme tak třeba, že bychom mohli rozdělit celý proud vzduchu na částice, jejichž pohyby jsme schopni pomocí kouřových stop, sledovat. Čím tenčí kouřové stopy dokážeme vytvořit, tím pravdivější obraz o dějích v proudícím vzduchu získáme. Čarám, které kouř ve vzduchu vykreslí, říkáme proudnice a jejich chování pak pozorně sledujeme.

Není-li v proudu vzduchu umístěné žádné těleso, měly by být proudnice vzájemně rovnoběžné. Pokud začnou proudnice vytvářet po proběhnutí určité dráhy zřetelné vírové pohyby, máme v ruce důkaz, že částice vzduchu se během svého pohybu posunují nejen ve směru , ke kterému je pobízí tlakový spád, ale že se ještě při tom otáčejí.

Abychom mohli dostatečně dlouho pozorovat děje v proudícím vzduchu, je třeba, aby se rychlost proudu neměnila nezávisle na naší vůli. Takovýto proud se stálou rychlostí nazýváme stacionární. Pokud se částečky vzduchu, vytvářející při svém pohybu proudnice, neotáčejí, nazýváme tento proud potenciálním. A zase jsme dva duchy zbavili jejich virtuality.

Nyní uvažujme o tom, že proudění vzduchu by nemělo jakkoliv nárazově kolísat. Mělo by se jen plynule měnit (někdy, ale i dost rychle). Zároveň by se nemělo měnit jeho množství ve sledovaném prostoru. Průtok by měl být v celém rozsahu spojitý. Připomeneme-li si ještě z dob školních lavic zákon o zachování energie( buď Lavoisiéra nebo Mendělejeva, že se nic nevytváří, nic se neztrácí a vše se jen přeměňuje) a smícháme-li tři uvedené věty do jedné myšlenky, pak jsme se dostali k tak zvané rovnici kontinuity.

Když ještě k tomu budeme souhlasit s tím, že není možné, aby jakákoliv energie samovolně vznikala nebo zanikala, pak jsme se právě podívali správným směrem a to přímo na rovnici Bernoulliho. U tohoto „pamětního místa“ se trochu zdržíme, protože to jeden ze základních klíčů k pochopení dějů v aerodynamice.

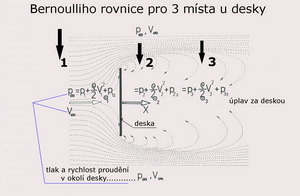
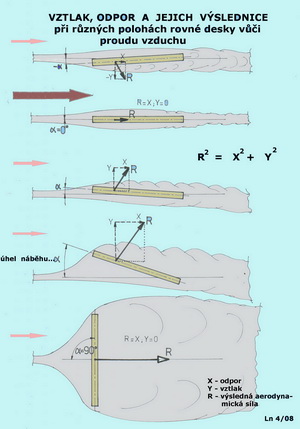
Při jakémkoliv proudění můžeme zaznamenat dva druhy tlaků. Tlak statický je prvním z nich a udává tlakové poměry uvnitř proudící tekutiny. Druhým je tlak dynamický, který zase vypovídá o možných vnějších účincích proudu. Jejich prostým součtem je celkový tlak proudící tekutiny. Jestliže je tekutina v klidu- neproudí, je tlak dynamický rovný nule a celkový tlak v tekutině se rovná tlaku statickému. Jakmile se tekutina, ať již kapalina či plyn, dá do pohybu začne se tlak statický zmenšovat. Jeho úbytek se změní v tlak dynamický. Velikost dynamického tlaku, vzniklého na úkor části tlaku statického, je přímo úměrná hustotě proudící kapaliny a druhé mocnině rychlosti proudu –ρ/2.V2.

Čím větší je rychlost proudění tím větší část tlaku statického se změní na tlak dynamický. Při nekonečně velké rychlosti proudu by se tedy veškerý tlak statický změnil v tlak dynamický. To ale dost dobře nejde, protože nemáme prostředky k tomu, abychom stvořili nekonečně velkou rychlost proudění hmotné tekutiny. Takže vždycky vedle sebe existují nějaký tlak statický a nějaký tlak dynamický. Jejich součet je pořád stejný a rovná se tlaku v okolní tekutině.

Velikosti obou tlaků jsme schopni změřit více méně přesnými nástroji. K určení statického tlaku nám postačí vhodný tlakoměr umístěný například ve stěně kolem níž tekutina proudí. Dynamický tlak jsme schopni změřit Venturiho, Pitotovou nebo Prandtlovou trubicí(rychloměrem). Existují již ale přesnější nástroje a metody.

Uveďme jednoduchý praktický případ. Mějme kupříkladu v nějakém místě na povrchu Země barometrický tlak třeba 1050hPa. Pak se dají masy vzduchu do pohybu vlivem všelikých tlakových níží a výší nad kontinenty a oceány, dejme tomu rychlostí 30m/s. A co nestane? Původní barometrický tlak (my víme, že to byl celkový tlak na tom místě a protože ovzduší bylo nehybné, byl to zároveň statický tlak) se zmenší. A sice o hodnotu asi 549 Pa. Takže citlivý barometr nyní ukáže tlak 1050 00 –549= 1 04451 Pa. Nad takovou malou změnou mávnete rukou pokud si nespočítáte dynamické účinky proudu vzduchu o rychlosti 30m/s. Takovýto proud působí na 1m² plochy kolmo postavené mu do cesty silou právě 549 N. To je síla významná a je rovna podle dřívějších výkladů fyzikálních jednotek cca 56kg. Zkuste takovou sílu udržet v rukách.

Podobně to funguje při proudění kolem ploch, které sestávají z jakýchkoliv vhodných tvarů. Kolem nich se vytvoří tlaková pole s rozdílnými tlaky, jež se snaží pohnout tělesem z místa vyššího tlaku na místo, kde je v jeho okolí tlak nižší. Protože obvykle působí tyto tlakové síly různými směry a mají rozdílné velikosti, mají snahu tělesa nejen posunout, ale i natočit.

Když chceme, aby se tělesa nepohybovala jak se zlíbí vzniklým tlakovým silám, ale jak požadujeme my, použijeme takové jejich tvary, které vedle síly působící ve směru proudu (tou silou je odpor bránící pohybu vpřed) dovolí vzniknou i síle na směr proudu kolmé, a tu sílu nazýváme vztlakem. Když je sečteme dostaneme výslednou aerodynamickou sílu působící na těleso. K tomu všemu ještě dostaneme do vínku moment, který se tělesem snaží otočit.

A teď zkusíme napovědět něco o tom co se to s tlakovými silami děje kolem profilu(křídla nekonečného rozpětí), jestliže se začne pohybovat vzduchem.

Již v 17. a 18. století legendární Newton a po něm Euler popsali některé tlakové a tím i rychlostní děje kolem těles obtékaných proudem tekutiny. Pak z toho vznikla Bernoulliho rovnice(viz dřívější zmínka i stať v naší kapitole „Slovník vybraných pojmů).

Přenesme se nyní se základní povědomostí o tom, že tlak a rychlost v proudící tekutině spolu bezprostředně souvisejí, k obtékání tělesa ve tvaru křídla nekonečného rozpětí - profilu. Změny tlaku v závislosti na změnách rychlostí vyvolávají na jeho povrchu síly z nichž vzniká (nebo také zaniká) především vztlak a pak také odpor. Jejich nerovnoměrné rozložení po horní a spodní straně vytváří dvojici sil- moment, který se křídlo snaží překlopit přední částí(náběžnou hranou) dolů nebo nahoru(podle tvaru střední křivky profilu). To je zopakování jedné části předchozího textu jinými slovy.

Čím je rychlost proudu vyšší, tím je v něm tlak, oproti okolnímu prostředí, nižší, ale dynamický účinek proudu( ρ/2.V2 - což je dynamický tlak) zase vyšší. Jejich součet je, i při započtení všelikých ztrát k nimž během proudění dochází, stále stejný a rovná se prvotnímu tlaku, který se uvolil být hybnou silou pro toto proudění. Ten je v proudu za obtékaným tělesem nižší o prve zmíněné ztráty vzniklé během jeho obtékání. Kdesi v nekonečnu se opět přečerpáním části energie z okolí dostane na původní hodnotu. A tak se ve skutečných, ne v ideálních, tekutinách „uplatňuje“ všudypřítomný odpor, jehož velikost můžeme odhadovat podle intenzity vírů za křídlem nekonečného rozpětí.

Co se tedy asi děje kolem profilu?

Pomozme si následujícím obrázkem, kde je velmi zjednodušeně zakresleno obtékání profilu tvaru rovné desky s neupravenou přední i zadní částí.

Je tu několik postavení desky vůči proudu vzduchu a k nim jsou přiřazeny přibližné hodnoty vztlaků a odporů, jakožto na desku působících sil. Je tu též uvedena výsledná aerodynamická síla R, která je geometrickým součtem obou předchozích.

Deska zaujímá vůči proudu vzduchu nejprve záporný úhel náběhu(nahoře), pak je rovnoběžná se směrem proudu(nulový úhel náběhu) a následně se její úhel náběhu zvětšuje nejprve málo, pak trochu víc, až dosáhne hodnoty devadesáti stupňů.

Všimněte si také jak velký vír vzniká za deskou při jejich různých postaveních.

Nyní pokládáme za vhodné znovu připomenout působnost Reynoldsova čísla na výsledky proudění kolem profilů, což má zásadní význam zejména pro malé a menší létající stroje(modely letadel). I když u některých skutečných letadel, například u malých hloubek konců jejich nosných ploch(zejména při velkých štíhlostech) není jeho vliv také zanedbatelný.

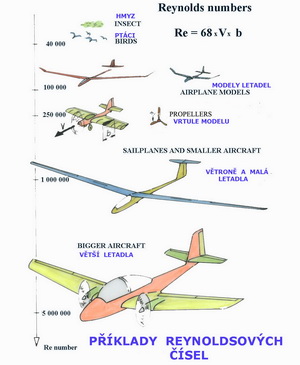
Z tohoto obrázku můžete získat povědomost o tom jakých asi hodnot Reynoldsových čísel mohou dosahovat různé objekty pohybující se v povětří Země. Je na něm také znovu uveden vztah pro výpočet tohoto bezrozměrného kriteria.

Nemohli jsme Re číslo znovu nepřipomenout, protože jak plyne z dalšího obrázku je závislost výsledné aerodynamické síly, zde zastoupené jejím součinitelem, některých těles na něm značná.

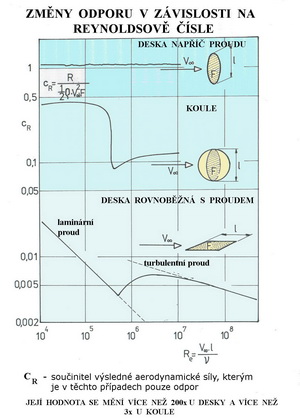
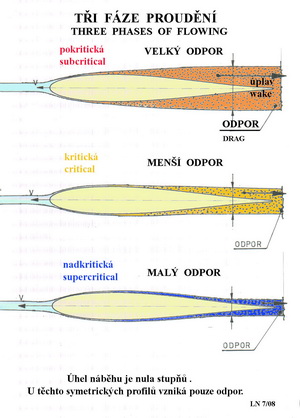
Pouze u desky postavené kolmo ke směru proudu je tato síla na Re čísle prakticky nezávislá. U koule je náhlá změna odporu při Re čísle kolem cca 350 000 obrovská. U desky rovnoběžné s proudem se mění velikosti cR rovněž dramaticky.

V tomto obrázku stojí mimo jiné za povšimnutí, že plocha F je u všech tří těles stejná. A také to, že ve spodní části jsou vzpomenuty dva druhy proudění-laminární a turbulentní(viz naše stať Slovník vybraných pojmů). S tím bezprostředně souvisí tři možné fáze prouděním kolem létajících strojů.

Ty jsou vzpomenuty na dvou dalších obrázcích.

První z nich zachycuje přibližné stavy proudění u symetrického profilu přiměřené tloušťky při nulových úhlech náběhu. Horní případ ukazuje, že proud není schopen sledovat oba povrchy profilu do větší hloubky a odtrhává se asi v jedné třetině hloubky. Je to typický příklad tzv. podkritického proudění, kdy je úplav – to jen ten vír za profilem, rozsáhlý a odpor proto velký.

Druhý případ zachycuje již vyvinutější stav proudu, který je již schopen sledovat povrchy profilu do větší vzdálenosti od náběžné hrany, zde asi do jedné poloviny hloubky profilu. Úplav se proto přiměřeně zmenšil a odpor proto také klesl. Toto je příklad nesčíslného množství malých modelů letadel. Ty vlivem malých hloubek ploch a nízkých rychlostí nedosahují potřebných hodnot Re čísel a výsledkem jsou nestálé výkony i letové vlastnosti. Často pomohou různé „přípravky“ k ovlivnění druhu proudění.

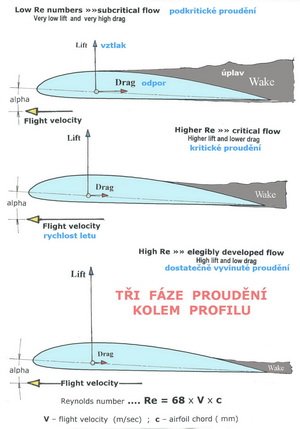
V obou těchto případech je velmi, ale opravdu velmi vhodné snažit se včas přeměnit, od povrchu k odtržení náchylný,laminární proud, který existuje při těchto nedokonalých obtékáních, v přilehlý proud turbulentní tím , že mu vložíme do cesty na povrchu profilu mechanickou překážku v podobě několik desetin milimetru tlusté a asi 3mm široké pásky (to platí pro menší modely), pro skutečné větroně jsou dimenze těchto turbulátorů větší. A to po tak velké části rozpětí nosné plochy kde k tomu může docházet. Ale o tom jsem již psal mnohokrát.

Dolní příklad v tomto obrázku již představuje proudění dobře vyvinuté, kdy se laminární proud(má-li pro to podmínky) vznikající v přední části profilu postupně změní v přilehlý turbulentní proud, je schopen sledovat povrch do značné vzdálenosti od náběžné hrany, aniž by se předčasně od něj odtrhával a působil tak neplechu jako v předchozích dvou případech. O takovýto druh vyvinutého, nejprve laminárního a následně turbulentního, proudění se snažíme vždy a to velmi iniciativně. I když to v některých případech není tak jednoduché.

Ještě poznámka – ve všech třech předchozích případech vznikal pouze odpor.

Na dalším obrázku jsou obdobné situace, jako prve, ukázány schematicky na profilu s prohnutím při menším úhlu náběhu. Zde již vzniká ve všech třech případech vztlak i odpor(ale i moment, o němž zatím pomlčíme).

V prvním případě shora se jedená zase o podkritické nevyvinuté proudění. Výsledkem je zase široký úplav, velký odpor a pouze malý vztlak.

V druhém případě je to již proudění trošku vyvinutější, ale stále ještě nestabilní a zrádné. Úplav se sice zmenšil, ale odpor střídavě klesá a zase stoupá ve spojitosti s opačnými změnami vztlaku. Letové výkony i vlastnosti jsou tak rozmanité, že znechutí mnoha adeptům leteckého modelářství pokračovat v tomto hobby dále. Jinak platí totéž jako v prostředním případě předchozího obrázku.

Poslední, spodní, fáze proudění je již pro létající stroje přijatelná a my se snažíme, aby tomu příslušná Re čísla jejich místních hloubek nosných a ocasních ploch byla co největší a aerodynamické jemnosti následně rovněž.

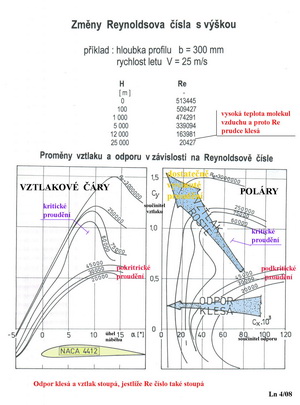
Z předchozího obrázku, ač jsme ho již myslím někdy uvedli, můžete načerpat informace o tom jak se mění Re číslo s výškou nad zemským povrchem pro plochu s hloubkou 300m pohybující se rychlostí 25m/s.

Ve spodní pravé části je pak instruktivní grafický argument o tom jak se mění součinitelé vztlaku a odporu (zastupující zde odpor a vztlak) v závislosti na velikostech Re čísel. Jsou zde označeny oblasti podkritického, kritického i dostatečně vyvinutého proudění pro profil NACA 4412.

Prameny
Bauer, Brůha, Jaňour-Základy proudění,r. 1950
vlastní archiv