Profily nosných a ocasních ploch
5. část

Asi již nastal čas, abychom napověděli něco o nalézání a ovlivňování aerodynamických charakteristik profilů, neboli o tom jak je nesnadné poznat vztlak, odpor a klopný moment a později i předpovědět jaké jejich typické vlastnosti lze nalézt na pozadí neustále se vyvíjejících technologií a materiálů.

Tak tomu bylo vždy od dob, kdy se průkopníci letectví začali systematičtěji zajímat o to, jak zlepšit výkony a letové vlastnosti létajících strojů. Začalo to tak trochu platonicky za Leonarda da Vinci na přelomu 15. a 16. století. Pak to byl Isaac Newton, který zapsal důležité okolnosti o odporu rovné desky do matematické formule. George Cayley na počátku 19. století již pochopil jak má asi vypadat profil nosné plochy létajícího stroje. Avšak teprve ke konci 19. století Otto Lilienthal dokázal létat na svahu za silnějšího větru. Mezitím se však již někteří z inženýrů pokoušeli získat údaje o vztlaku a odporu nosných ploch pomocí „koloběhů“ či později nedokonalých větrných tunelů. Zpočátku to šlo ztuha, ale nějaké výsledky byly získány a na pozadí dosažených experimentů odvážných borců byly postupně včleněny do poznávaní základů létání.

Proč o tom píši znovu? Je to jen proto, že bych si chtěl připravit výchozí postavení k připomenutí nástrojů, které pomáhaly v zemích, jež měly dostatek peněz na výzkum, a dodnes nejsou bez zaměstnání(ty nástroje), získávat údaje pro létání nejcennější. Jsou to aerodynamické tunely, jichž byl postaven značný počet na celém světě. Já sám jsem měl dokonce tolik touhy poznat jaké to asi může být, když si postavím svůj vlastní větrný tunel. Bylo to bláznivé, ale úžasné, několikaleté dobrodružství, které mohou někteří „znalci“ zpochybnit. To mi nevadí. Mám to totiž již více než 25 let za sebou a zůstává mi z toho docela dobrý pocit, že je možné dosáhnout i zdánlivě velmi obtížného, s přijatelnými výsledky.

Je to malé odbočení od vlastních profilů, ale myslím, že stojí za to připomenout stručně jak to asi bylo.

Začalo to jakýmisi koloběhy, což byla rotační zařízení, uváděná obvykle do rovnoměrného pohybu závažím (podobně jako u hodin „pendlovek“), opatřená ramenem na jehož konci byl upevněn testovaný předmět.K tomu docházelo již v druhé polovině 18. století, když se začal zkoumat odpor dělových koulí prodírajících se vzduchem směrem k protivníkovým postavením. Výsledky ale asi nebyly příliš vypovídající.

Pak pocítili potřebu poznat aerodynamické síly a momenty všichni průkopníci letectví v 19. století, protože přece jenom k nim nějak dolétly nápady G.Cayleyho o tom, že profil nosné plochy má mít nějaké prohnutí a také určitou tloušťku. Mnoho nadšenců, vycházejíc snad z poznatků Newtonových, aplikovalo na nosné plochy obrovských rozměrů rovnou desku, coby profil. To nemělo pražádnou šanci na úspěch. Například A.Pénaud zhruba v polovině 19.století již předvedl funkční let modelu s tenkým prohnutým profilem nosné plochy, ale stále se neznala podstata vztlaku. Té síly, která by vyrovnávala účinky zemské tíže.

O.Lilienthal se svým bratrem v posledním desetiletí téhož století již vycítili správný směr, ale přesto při svých pokusech používali, zejména zpočátku, také jen nějaký, i když zdokonalený koloběh.

Ponecháme historické zpracování těchto pomůcek stranou a přistoupíme rovnou k pokusům bratří Wrightů, kteří jakousi větrnou troubu ze dřeva sestrojili a poznatky o vztlaku a odporu se pomocí modelů křídel z ní snažili vypáčit. Výsledky byly nevalné, jak sami později řekli, ale něco se přeci jenom dozvěděli. Přinejmenším vyloučili několik „slepých uliček“ do nichž by jinak snadno zabloudili. Jejich větrný tunel je na následujícím obrázku.

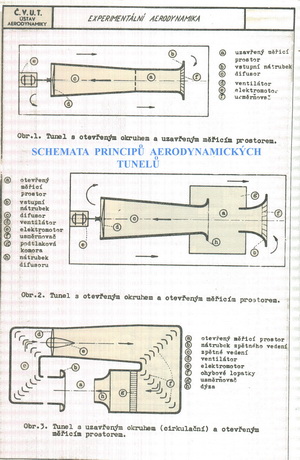
Když přeskočíme několik let a pak ještě několik desítek dalších, kdy bylo vybudováno množství již celkem použitelných zkušebních zařízení-tunelů, můžeme na následujícím obrázku poznat tři z více možností, jak takový aerodynamický tunel navrhnout. Na obrázku je dostatek textu, takže není třeba dalších komentářů.

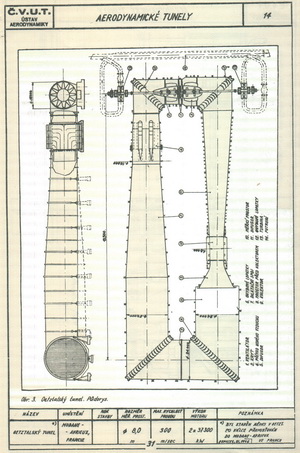
A na dalším obrázku je již schéma velkého beztlakého tunelu, jenž jako válečnou kořist instalovali Francouzi po 2. světové válce v Modane Avrieux. Všimněte si například výkonu potřebného k získání a udržení obrovské rychlosti v tak velkém průřezu. Výkony hnacích ústrojí ještě větších amerických tunelů z té doby vyžadovaly již příkon více než 120 000HP. To by stačilo pro dvě 100W žárovky v každé domácnosti milionového města.

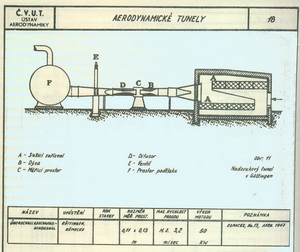
Předchozí dva obrázky a také ten následující, jsem použil ze skript strojní fakulty Českého vysokého učení technického v Praze, které jsem získal, když jsem navštěvoval nepovinné pozdně odpolední přednášky z aerodynamiky v roce 1953-54, které organizoval pan profesor Rudolf Pešek, šéf katedry thermo a hydromechaniky. Za to jsem jemu a pracovníkům jeho katedry vděčný nejen já, ale i zhruba 30 dalších studentů pražské strojní fakulty. V té době měla právo poskytovat vysokoškolské vzdělání pro letectví již jen VTA Brno. V Praze jsme byli předurčeni k tankovým vojskům, což jsme si dostatečně, během 5 let, užili.

Protože již v rozmezí let 1940 až 1944 dosáhli Němci významných poznatků a nakonec i úspěchů v létání rychlostmi nad 200m/s(720km/h) a poměrně úspěšně, ale lidsky bezcitně, využívali i rakety V-2, nebylo divu, že k tomu potřebovali také vhodné tunely pro vysoké rychlosti.Zjednodušené schéma jednoho z nich je na následujícím obrázku.

Obrovské úsilí v hledání aerodynamických charakteristik profilů, ale nejen jich, bylo vynakládáno v USA. Již před 2.světovou válkou, kdy byla světu představena 4-místná řada profilů NACA různých prohnutí a tlouštěk, založená na systematickém zkoumání jejich vlivů. Tunely byly schopny simulovat podmínky pro Reynoldsova čísla od cca 700 000 přes 10 000 000. Výsledky byly publikovány v NACA Reportech dostupných i mimo USA. Jedním z nejznámějších byl Report No. 824 od autorů I.H.Albota, A.E, von Doenhoffa a L.S Stiverse Jr. Z roku 1945. Z něj čerpali všichni českoslovenští stavitelé letadel po mnoho let. Já jsem jednu z kopií získal z NACA v roce 1970.

Jaká laboratorní monstra byla v té době stavěna je zachyceno na příkladech tunelů v Ames. Jeden z nich měl rozměry měřícího prostoru 7 x 10 stop a maximální zde dosahovaná rychlost proudu byla 250 mph(cca 400km/h). A to v roce 1941.

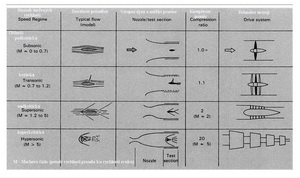
Další schéma přináší velmi stručné informace o několika druzích tunelů, ať již podzvukových, beztlakých či přetlakových, které charakterizuje (to schéma) období od cca 1925 do 1960.

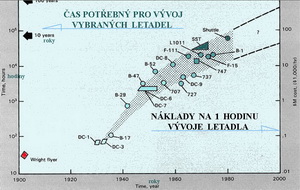
Testování celých letounů, nebo jen jejich částí, v tunelech vyžaduje vedle kvalifikovaných týmů, značné finanční prostředky a stále delší období pro řešení nových a složitějších problémů. To se snaží prokázat další schéma, které je velmi poučné a dokazuje, že nákladný výzkum v letectví si mohou dovolit jen velmi bohaté země. To mi připomíná jedno rčení, které jsem pochytil z druhé ruky. Ptal se jeden člověk druhého, při přátelské debatě, jestli zná nějaký příklad rychlého bankrotu. Ten uváděl jen jakési přízemní důvody. Načež se mu dostalo následujícího instruktivního ponaučení: Chceš-li jistě a poměrně rychle skončit jako podnikatel, vlož svoje prostředky do leteckého výzkumu a vývoje.

V tomto schématu je na levé souřadné ose logaritmická stupnice skutečné doby strávené při výzkumu a vývoji amerických letadel označených uprostřed diagramu. Vlevo dole se začíná s Flyerem bratří Wrightů. Na vodorovné ose dole jsou vynášena časová období, kdy k vývoji docházelo. Pravá osa souřadného systému ukazuje na logaritmické stupnici jaké měrné náklady bylo třeba vynaložit na hodinu práce. U Wrightů to byly jednotky dolarů, u B-17 stovky dolarů, u B-727 tisíce a u B-1 desetitisíce dolarů na jednu hodinu výzkumu a vývoje. Projekt Shuttle spolykal již 80 000 dolarů na hodinu potřebnou pro jeho stvoření. To jsou hrůzostrašná čísla pro příslušníka malého státu, byť i třeba úspěšného vývozce ultralightů.

Než opustíme nepatrnou exkurzi k aerodynamickým tunelům je vhodné ještě poznamenat:

- je to záležitost nákladná, zdlouhavá a vyžaduje velmi kvalifikované lidi

- bez této nákladné lidské činnosti se však ani budoucí vývoj v letectví zřejmě neobejde

- dosavadní výpočetní metody suplující výsledky měření v tunelech jsou stále spolehlivější, ale na všechna řešení, byť i jen metodou postupných přibližování, pravděpodobně nestačí

- s měřeními v tunelech všelikých tvarů, velikostí a používaných způsobů simulace předpokládaných situací a jejich vyhodnocováními to ale není tak jednoduché. Není to zase úplně z dávnověku letectví, kdy se například nepřisuzovalo stupni turbulence proudu vytvářenému hnacím ústrojím a vnitřními vestavbami tak velký vliv. A byl tu. Zjistilo se také, že hluk způsobený rychlým proudem má rovněž vliv na výsledky měření. O udržení stálé teploty a rychlosti proudění ani nemluvě. Nepříznivý vliv mohou snadno mít malé rozměry tunelu, kdy jeho stěny při větších úhlech náběhu ovlivňují přirozené obtékání profilu, atd.

Druhý způsob jak se dostat k aerodynamickým charakteristikám profilů jsou výpočetní metody, dnes doprovázené programy, které umožňují více či méně přesné jejich určení. Spolehlivé jsou poměrně dost při malých úhlech náběhů a dostatečně velkých Re číslech. V ostatních oblastech se již zřetelněji odchylují od hodnot získaných v tunelech nebo při testování ve volné atmosféře na skutečných letadlech, případně na jejich dostatečně velkých modelech. Je ovšem diskutabilní jaké možnosti byly při testech v tunelech nebo ve volné atmosféře k dispozici, jaké korekce naměřených hodnot a metody vyhodnocování výsledků použity.

Mezi nejznámější programy k získání aerodynamických charakteristik profilů náleží americký - „X.foil“, prof Drely a z toho odvozený a trochu zjednodušený italský – „Profili“ , Dr. Durantiho. Existují ještě i jiné, více či méně složité a na výpočetní techniku náročné, programovací pomůcky.

Takže jsou to aerodynamické tunely a počítače s vhodnými programy, které jsou schopny napovědět jak to třeba vypadá se vztlakem. I když jsme to již dříve uvedli zopakujme to trochu jinak. Vztlak je síla, kterou potřebujeme k tomu, abychom překonali nepříznivé účinky zemské tíže a některých dodatkových sil vzniklých za pohybu létajícího stroje těžšího vzduchu a dokázali létat podle naší vůle(což se někdy nepříliš daří).

Spokojme se s konstatováním, že vztlak vznikne jakožto součet rozdílných tlaků působících nad horním a pod spodním povrchem nosné plochy. Vznikají tak dvě síly působící obvykle souhlasným směrem, někdy však ve smyslu opačném a pak je jejich účinek zeslaben tak, až žádný vztlak nevzniká.

Nosná plocha by při tom měla být vybavena vhodným profilem, který v závislosti na úhlu náběhu, který svírá se směrem letu, poskytuje dostatečný, malý nebo žádný vztlak.

Rozdělíme-li profily(křídla nekonečných rozpětí, však již víte) na tři skupiny(ty už také znáte) podle tvaru prohnutí jejich středních křivek, dostáváme se k jejich třem známým zástupcům.

Jsou to profily souměrné(symetrické), jejichž prohnutí je nulové a střední křivka má tvar přímky.

Druhou skupinu tvoří profily s jednoduchým(kladným) prohnutím nepřesahujícím obvykle 7% hloubky profilu. Střední křivka má tvar vypuklý s maximem někde mezi náběžným a odtokovým bodem profilu.

Třetí skupinu tvoří profily s dvojitým prohnutím(ve tvaru S) střední křivky. Jejich střední křivka dosahuje v přední části tětivy profilu maxima a v její zadní části minima prohnutí. Jsou to tak zvané „autostabilní“ profily.

Vystavíme-li tyto profily účinkům proudu vzduchu(buď v tunelu nebo virtuálně v počítači) při různých úhlech náběhu můžeme poměrně snadno zjistit jakou jsou schopny zajistit vztlakovou sílu. Každá z uvedených skupin sílu jinou, viz následující obrázek. Jsou ze uvedeny jako vztlakové čáry(křivky).

Doporučuji, ještě než budete pokračovat ve čtení, abyste se podívali zpátky na magazín AL 7/08 a AL 9/08 do článků o profilech nosných a ocasních ploch.

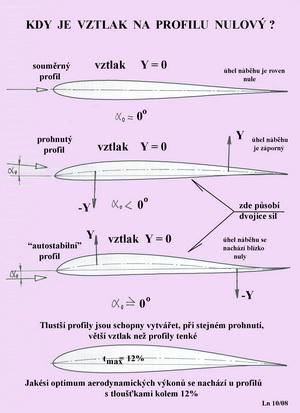
Na tomto obrázku je síla zastoupena koeficientem vztlaku(stejně tomu bude u odporu a momentu), který je vynášen na svislou osu. Je to bezrozměrná hodnota výhodně použitelná pro další výpočty výkonů a vlastností letadel. Všimněte si, že v okolí malých(i záporných) úhlů náběhu, zde v rozmezí cca minus 5 stupňů až plus osm stupňů, má přímkový průběh. Podmínkou však je dostatečně vyvinuté proudění(dostatečně velké Re číslo). U Re čísel nad asi 1 000 000 je rozsah přímkové části větší. U malých modelů letadel to ale neplatí. Zde je tato část dost pokřivena a tvaru přímky vzdálena.

Sklon( směrnice) vztlakové čáry může mít teoreticky hodnotu 0,11. Znamená to, že každá změna jednoho stupně úhlu náběhu mění velikost vztlaku o cca 10% oproti stavu předešlému. A to jak nahoru-zvětšování vztlaku, tak dolů-zmenšování vztlaku. Ve skutečnosti je to méně a to tím více, čím je proudění méně vyvinuté. Maximálně dosažitelné součinitele vztlaku při dostatečně velkých Re číslech mohou dosahovat hodnot v rozmezí 1,5 až 2, bez potřeby využívat změnu geometrie původního profilu(klapky, sloty apod).

Uvedl jsem sem záměrně určitý rozsah možných vztlakových křivek, protože jejich bod společný s osou vodorovnou(kdy je vztlak roven nule) se posunuje vlevo či vpravo, podle tvaru a velikosti prohnutí. Jsou to nám již známé úhly náběhu při nulovém vztlaku.

Jejich hodnoty u profilů s kladným prohnutím, v obrázku s označením 2 najdeme vždy vlevo od nulového úhlu náběhu. Úhly náběhů těchto profilů jsou pro nulový vztlak vždy záporné.

U profilů souměrných, v obrázku s označením 1, to bude vždy právě při úhlu náběhu rovném nule. Tak je snadno poznáte, když by vám někdo předložil vztlakovou křivku profilu neznámého tvaru.

Profily s dvojitě prohnutou střední křivkou, označené zde číslicí 3, mohou vykazovat při nulovém vztlaku hodnoty úhlů náběhů pohybující se v okolí úhlu náběhu rovném nule a to vlevo i vpravo. Vpravo v případech velkých Re čísel.

Vztlak jakožto výsledek působení tlaků nad horní a pod spodní stranou profilu nemá u prohnutých profilů stálé působiště a působí kolmo na směr pohybu(letu). Pohybuje se dopředu či dozadu na tětivě profilu. U všech profilů má hodnoty kladné i záporné a mezi nimi samozřejmě hodnotu nulovou. Podívejte se na následující obrázek, kde jsou stručně popsány stavy kdy vztlak jako výsledná síla z profilu zmizí. Je nulový. Ale působící síly nulové nejsou.

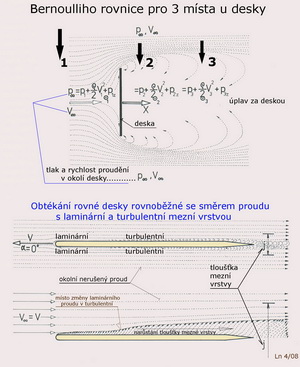
Dvojice sil vzniklé na prohnutých profilech při určitém úhlu náběhu se navzájem ve svém silovém účinku ruší. Ne však moment, který vyvolávají. Ten provází profil neustále a je nutno jej zahrnout do celkové momentové charakteristiky profilu. Nazývá se momentem při nulovém vztlaku a označuje se obvykle jako m_z0.

Moment, který vzniká působením vztlakové síly, se snaží profilem pootočit. Viz předchozí obrázek. A jak toto otočení profilem proti směru hodinových ručiček nebo v jejich směru můžeme určit??? To znamená zjistit v případě skutečné nosné nebo ocasní plochy namáhání jím vyvolané. Zkrátím teoretizování, protože již jsme poznali aerodynamický střed profilu a jeho místo na tětivě. To umožňuje výhodnou úvahu kdy nahrazujeme skutečnou polohu vztlaku tak, že ve výpočtech použijeme hodnotu m_z0, jehož hodnota je stálá a je ovlivněna především tvarem střední křivky profilu a vztlak „umístíme“ do aerodynamického středu. Při změnách úhlů náběhu si pak již všímáme pouze změn velikostí vztlaku. Proto je důležité vědět při jakém úhlu náběhu je vztlak roven nule a jaký tomu odpovídá moment.

A nyní zbývá všimnout si znovu trochu blíže odporu, který nás pronásleduje stále jakmile se pohneme. A totéž platí i o profilech(křídlech nekonečných rozpětí). Protivný odpor nám brání v jednoduchém a levném pohybu ovzduším Země a proto se ho snažíme jakýmkoliv vhodným způsobem omezit. Odstranit úplně, ho neumíme. Abychom byli objektivní je třeba přiznat, že ho občas i využíváme, jestliže potřebujeme rychlost pohybu letadla zmenšit nebo například délku přistávací dráhy zkrátit.

V podstatě existují dvě příčiny odporu s nimiž se musíme vypořádat. Připomeňme si je již dříve uvedeným, následujícím obrázkem.

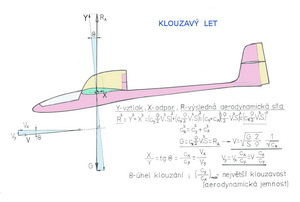
Jak jsme již naznačili dříve, při zmínce o mezní vrstvě proudu, je to vnitřní tření (vyjádřené vazkostí) tekutiny, které se zde při tom uplatňuje a ovlivňuje podmínky pro vznik laminárního či turbulentního proudění. Takovýto odpor, někdy zvaný třecí, tvoří jednu část celkového odporu profilu.

Částice tekutiny procházející mezní vrstvou, ať již laminární či turbulentní, ztrácejí v ní postupně svoji energii vlivem tření a pokud se neodtrhnou od povrchu profilu(křídla) již před jeho odtokovou hranou vytvářejí vírovou stopu zvanou úplav i za velmi dobře tvarovaným tělesem. Tlak v úplavu je nižší než tlak v proudu nabíhajícím na profil. Z jejich rozdílu pak vzniká síla působící proti směru pohybu(letu), jejíž prvotní příčinou je vazkost tekutiny a tato složka tlakového(tvarového) odporu doplňuje v celkovém odporu složku třecího odporu. Ten působí, jako jeho obě složky, proti směru pohybu a rovnoběžně se směrem pohybu(letu). Je kolmý na vztlak.

Nejmenší dosažitelné celkové součinitele odporu se pohybují, při dostatečných Re číslech, kolem hodnot 0,004 – 0,005.

A jak teď dál???

Dobrali jsme se trochu rozsáhlejším nicméně stále velmi populárně podaným výkladem ke vzniku a existenci dvou aerodynamických sil a momentu, které jsou typické pro profily nosných a ocasních ploch.

Když máme dvě síly jsme schopni je posoudit společně, tj. sloučit je. Protože je obvykle znázorňujeme jako vektory( mají směr a velikost) a obě spolu svírají pravý úhel můžeme je sečíst snadno graficky nebo algebraicky pomocí Pythagorovy věty. Sílu takto získanou nazýváme výslednou aerodynamickou silou. Ta svírá se směrem letu již menší než pravý úhel. Čím je tento úhel menší, síla je více skloněna dolů, tím jsou aerodynamické výkony profilu horší. To zachycuje další obrázek se spoustou důležitých poznámek, které by mohly být čtenáři, v zájmu snazšího pochopení populárního povídání o letadlech, se zaujetím prohlédnout.

Dostali jsme se,“No konečně“ oddechnou si mnozí, k tomu co můžeme poznat na profilu a použít pro další zkoumání létajících strojů, pokud se týče jejich výkonů a vlastností. A to by mohlo být příště.

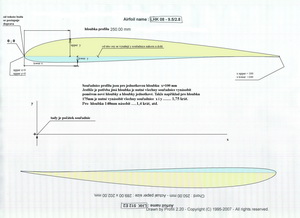
Dodatek této části,

který mě napadl po některých dotazech.

Může se stát, že někteří letečtí nadšenci se nemohou zcela srovnat s tím jak vykouzlit ze souřadnic obrysy profilů. To je dost omezuje v jejich úsilí a proto bych rád uvedl stručnou instruktáž, jak profily kreslit i když dost, spíše více, zájemců má odpovídající programy pomocí nichž tvary profilů ze souřadnic, pro různé hloubky, velmi rychle získá.

Tvary(obrysy) profilů jsou popsány dostatečně přesně jejich souřadnicemi v systému dvou os – x a y. A to jak jejich horních tak i dolních stran. Je třeba se smířit s tím, že počet bodů, které popisují souřadnice je více než 50, někdy podstatně více.

Zůstaneme u podkladů, které začínají počátkem obou souřadnic - x a y, kdy u novějších profilů jsou to hodnoty : horní strana x=0 ; y=0, dolní strana x=0 ; y=0, čímž je určen náběžný bod profilu.

Poslední vodorovnou ( x ) souřadnicí je pak hodnota : horní strana x=100, dolní strana x=100.

Svislé, neboli -y souřadnice se již nyní mohou od nuly lišit podle tloušťky odtokové hrany(křídlo nekonečného rozpětí=profil) a mohou mít kladnou i zápornou hodnotu. Viz připojenou tabulku souřadnic profilu LHK 512 E2.

Mezi těmito dvěma vodorovnými souřadnicemi, což je hloubka profilu, se nacházejí další desítky údajů pro horní(upper angl. výraz) a spodní(lower rovněž angl. výraz) stranu profilu. Vodorovné souřadnice mohou být společné vždy pro horní a spodní stranu, ale nemusí to tak být vždycky.

K předepsané vodorovné souřadnici x přiřadíme při kladné hodnotě y- ové souřadnice nad osu x příslušnou vzdálenost y upper. Tam je jeden bod horní strany profilu. Pro zápornou hodnotu y lower pak vynášíme příslušnou hodnotu pod osu x, kde je jeden bod dolní strany profilu. Tak postupujeme pečlivě a trpělivě vynášíme všechny body horního i spodního obrysu. Ty pak spojíme tenkou plynulou čarou.

Nenechte se vyvést z míry třeba tím, že v přední části profilu je hustota souřadnic podstatně vyšší než v jeho středu či ke konci. Je to tím, že přední část profilu, asi do 25% jeho hloubky, je třeba popsat přesněji, protože ta ovlivňuje jeho výkony a vlastnosti nejvíce.

Každá tabulka souřadnic tohoto systému má x-ové souřadnice v rozmezí 0 až 100. Y-nové souřadnice pak v rozmezí 0 až + nebo – nějaké číslo. Jejich absolutním součtem získáte tloušťku profilu v daném místě jeho hloubky.

Co ale teď, jestliže nechceme mít hloubku profilu 100mm. Když budeme potřebovat profil s hloubkou větší než původních 100, tak jednoduše tuto novou hodnotu podělíme 100. Získáme tak koeficient větší než 1, kterým pak vynásobíme všechny souřadnice, bez výjimky.

Uveďme jednoduchý příklad. Chceme vykreslit profil s hloubkou 850mm. Jeho původní souřadnice (vybereme namátkou) jsou : x= 45 ; horní strana y= 7,65 a spodní strana y =– 1,87.

Nové souřadnice pak musí být : x= 45 x 8,5= 382,5mm ; horní strana y= 7,65 x 8,5= 65,025 a spodní strana y= -1,87 x 8,5= -15,9mm.

A tak , sice poněkud zdlouhavě, ale úspěšně získáme všechny body obrysu profilu, které spojíme plynulou čarou. U hloubky menší než 100mm postupujeme stejně jen s tím rozdílem, že koeficient je menší než jedna.

Přikládám jeden obrázek, kde jsou obdobné instrukce pro kreslení profilu uvedeny.

A toto jsou souřadnice jednoho z nich. Soubor ke stažení

	Airfoil name : LHK 605m

Upper  X 	 Upper Y 
 0.00000	0.00000
 0.06700	0.30230
 0.20000	0.57000
 0.50000	0.96000
 1.00000	1.40000
 2.00000	2.04000
 4.00000	2.96000
 7.00000	3.92000
 10.00000	4.62000
 15.00000	5.44000
 20.00000	5.96000
 25.00000	6.26000
 30.00000	6.40000
 35.00000	6.42000
 40.00000	6.33000
 45.00000	6.15000
 50.00000	5.88000
 55.00000	5.53000
 60.00000	5.10000
 65.00000	4.61000
 70.00000	4.06000
 75.00000	3.48000
 80.00000	2.87000
 85.00000	2.22000
 90.00000	1.55000
 95.00000	0.85000
 98.00000	0.41000
 100.00000	0.10000

 Lower X 	Lower Y
 0.00000	0.00000
 0.04810	-0.25420
 0.20000	-0.44000
 0.50000	-0.64000
 1.00000	-0.84000
 2.00000	-1.08000
 4.00000	-1.36000
 7.00000	-1.60000
 10.00000	-1.73000
 15.00000	-1.83000
 20.00000	-1.83000
 25.00000	-1.77000
 30.00000	-1.69000
 35.00000	-1.58000
 40.00000	-1.45000
 45.00000	-1.29000
 50.00000	-1.12000
 55.00000	-0.93000
 60.00000	-0.72000
 65.00000	-0.48000
 70.00000	-0.26000
 75.00000	-0.07000
 80.00000	0.08000
 85.00000	0.18000
 90.00000	0.22000
 95.00000	0.14000
 98.00000	0.03000
 100.00000	-0.10000