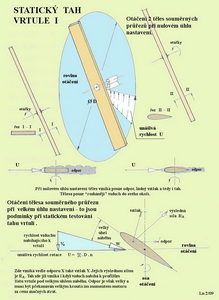
Statický a využitelný tah vrtulové pohonné jednotky

Pokusme se vysvětlit jaký je rozdíl mezi hodnotou tahu získanou prostým měřením síly na nepohyblivém zařízení v závislosti na otáčkách a využitelnou hodnotou tahu za letu.

Stále je totiž vžitý způsob posuzování kvality vrtulové pohonné jednotky hodnotou statického tahu. To je sice zajímavý údaj, který však nemá zvláštní vypovídací schopnost. Tj., nedokáže nás informovat o tom co a jak se bude dít za letu, což je ovšem velmi důležité, protože potřebujeme vědět například jakou rychlost letu můžeme dosáhnout s použitou vrtulí, při jakých otáčkách a jaký využitelný výkon jednotka může ještě poskytnout. Pokud vůbec ještě může.

Potřebujeme pro to znát průběh výkonu motoru v závislosti na otáčkách a účinnost celé jednotky. A to pro zvolený průměr vrtule. Ten můžeme měnit a sledovat jaké změny to vyvolá ve výkonu motoru a tomu odpovídajících otáček.

Výkon motoru a související otáčky můžeme získat některou z uznávaných metod. Pro spalovací motory například na brzdě a pro motory elektrické násobením přiváděným proudem, napětím a účinností. K tomu vždy přiřadíme otáčky provázející tento proces. Průměr vrtule je dalším parametrem, který k tomu potřebujeme. Stoupání vrtule bude mít poněkud menší vliv na průběh otáček a výkonu než její průměr, ale ve zpřesňovaní fázi testů bychom je měli měnit tak, abychom optimalizovali statický test co nejlépe.

K sepsání tohoto nevědeckého příspěvku mě vedou dvě okolnosti:

-první z nich je uvádění údajů všelikých výrobců pohonných jednotek o výsledcích statických testů jimi vyráběných pohonných jednotek a jejich neustálé přemílání mezi těmi, co mají zájem si nějakou jednotku opatřit pro svůj létající stroj, ať malý či skutečný

-moje málo úspěšná argumentace v diskuzích s mnoha stoupenci letectví a vrtulových pohonných jednotek o tom, že je to ve skutečnosti jinak. Prostě tomu nevěří. Nedaří se je příliš přesvědčit, ani když jim to předvedu ve svém malém jednoduchém tunelu. Nejprve maximálně dosažitelný statický tah s přívodním proudem a napětím při nulové rychlosti proudu vzduchu v tunelu. A pak pro tytéž otáčky nové údaje o ještě využitelném tahu, proudové spotřebě a napětí když uvedu proud vzduchu v tunelu do nějaké rychlosti(simulace letu).

Snad se mi povede trochu víc pomocí tohoto článku pro nějž jsem stvořil několik instruktivních obrázků. Sám jsem zvědav jak to dopadne.

Můžeme začít třeba takto: mějme k dispozici spalovací motor libovolného výkonu a opatřeme jej na jeho hřídeli dobře upevněnou a vyváženou dřevěnou latí o zvoleném průměru. Dřevěná laťka, dostatečné pevnosti, má stálý obdélníkový průřez a je upevněna tak, že je postavena svoji úzkou stěnou proti směru připravovaného otáčení. Viz následující obrázek.

Po spuštění motoru, doporučuji důrazně stát za ním, sledujme otáčky nejlépe pomocí otáčkoměru. Dřevěná laťka začne rozhánět okolní vzduch do stran a rámusit s rostoucími otáčkami víc a víc. Hluk začne být čím dál méně snesitelný až, pokud je výkon motoru dostatečný, dojde k nadzvukovému třesku a prudké bolesti v uších. Právě byla překročena konečky laťky rychlost zvuku. A tomuto stavu odpovídaly nějaké otáčky a výkon motoru.

Byl jsem jednou, před více lety, přímým divákem takovéhoto testu. Dřevěnou laťkou byl mučen jeden z tehdejších motorů MVVS pro závod kolem pylonů.

Při takovém pokusu vzniká, odmyslíme-li si hluk, pouze odpor jakožto výsledek obtékání hranaté laťky. Podmínky obtékání laťky jsou však již velmi komplikované, protože při tak velkých rychlostech mění vzduch svoje některé fyzikální vlastnosti. Je to ten případ vlevo nahoře v předchozím obrázku.

Když nahradíme hranatou laťku deskou stejného průměru i hloubky opatřenou symetrickým profilem, pravá horní část obrázku, pak při opakování pokusu dosáhneme stejného zvukového efektu při menším výkonu a přibližně stejných otáčkách. Předchozí zvětšující se hluk nebude takové intenzity, protože odpor této profilované desky je mnohem menší.

Ani v tomto případě však nevzniká jiná aerodynamická síla než odpor. Vzduch jakožto poddajné prostředí na něž chceme svými nápady zapůsobit se vůči rotující desce nijak zvlášť nezachová. Až na okrajové víry a jeho tenkou vrstvu unášenou rotující deskou se bude k ní chovat celkem netečně.

Pokud by v tom někdo nalezl zalíbení může testovat motor deskami různých tvarů i průměrů, až případně do jeho úplného zničení. Pokud při tom bude schopen zaznamenávat příkon a otáčky získá zajímavé údaje. To je mimo jiné, případ rotorů vrtulníků, opatřených symetrickými profily, nastavených v rovině otáčení pod nulovým úhlem náběhu.

Ale co se stane jestliže profilovanou dřevěnou desku nastavíme pod jiným než nulovým úhlem náběhu v rovině otáčení? To je zachyceno ve spodní části předešlého obrázku.

Zde již vznikne vedle odporu i vztlak, jejichž součtem je výsledná aerodynamická síla R_A. Posuzujeme-li nyní tuto zkroucenou desku obdobně jako dvě poloviny křídla letounu pak seznáme, že před ní vznikne podtlak a za ní přetlak. Součet těchto tlaků, který je způsoben výkonem motoru vloženým do této soustavy, působících ve stejném smyslu(dozadu za desku) na její rotující plochu vede ke vzniku tahu.

Deska se sice otáčí, ale stojí na místě. Nekoná tedy žádnou práci. Její účinnost je proto nulová. Spotřebovává pouze energii z motoru. Statický tah je nyní za daných podmínek(otáčky, nastavení obou polovin desky, její plocha apod.) největší.

Jaký je rozdíl oproti situacím uvedeným nahoře v obrázku?

Vzduch nyní procházející kruhovým průřezem rotující desky, která ho urychluje vlivem nakroucení obou polovin, má před ní již určitou rychlost V₀. Ta zde spolupůsobí s rychlostí unášivou U a jejich součtem je výsledná rychlost W vzduchu nabíhajícího k náběžné hraně desky. Ten svírá s tětivami souměrných profilů desky velké úhly náběhu a to tím větší, čím více se blížíme jejím okrajům. Výsledná aerodynamická síla je odkloněna výrazně proti smyslu otáčení a signalizuje, že odpor je v tomto případě příliš velký, protože proudění nestačí sledovat obrysy desky a odtrhává se od ní za vzniku mnoha vírů a ztracené energie.

V dalším obrázku je již posuzována vrtule, u níž se na rozdíl od předchozí nezkroucené desky, úhly nastavení po průměru mění, takže jsou schopny se všechny pohybovat po stejné šroubovici vytvořené postupným a unášivým pohybem. To u prve nezkroucené desky nebylo.

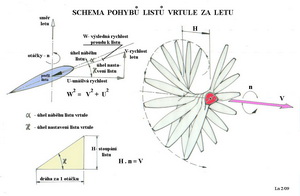
V horní části tohoto obrázku je znovu připomenut přímkový průběh unášivých rychlostí listu vrtule. Ty se mění od nuly ve středu otáčení do maxima na okrajích každého listu.

Ve střední části obrázku je příklad toho jak se mění úhel náběhu proudu vzduchu nabíhajícího k vrtuli. Čím blíže ke středu vrtule tím je tento úhel větší a příslušná část listu vykazuje značné ztráty. Naopak čím dále od středu tím jsou podmínky obtékání profilů listu relativně příznivější, i když mají k optimu dost daleko. Zvolme v našem příkladu řez přibližně v místě označeném 4. Tomu na poláře profilu vpravo (dolní část obrázku) odpovídá nějaká hodnota maximálního součinitele výsledné aerodynamické síly c_R.

Postoupíme-li vlevo do diagramu vztlakové čáry profilu zjišťujeme, že se nacházíme daleko za hodnotou úhlu náběhu příslušejícího možnému maximálnímu součiniteli vztlaku. Tam ale být nechceme. Potřebujeme se dostat na levou horní část vztlakové čáry profilu. To ale statická zkouška tahu vrtule neumožní, protože jen některé úseku vrtule jsou obtékány pod příznivějšími úhly náběhu. Proto jsou výsledky statických testů vrtulí do značné míry odlišné od jejich skutečných výsledků za letu.

Teď následuje pokus o trochu jiný působ vysvětlení funkce vrtule ve srovnání s předchozím.

Jestliže chceme k pohonu létajících strojů využít principu akce a reakce, kdy je pohonnou jednotkou uváděno do pohybu značné množství hmoty ne příliš velkou rychlostí dozadu za letadlo, tak využijeme schopností, kterou poskytuje vrtule.

Jak asi pracuje takový element letadla je uvedeno schematicky v následujícím obrázku, kde je zachycen šroubový pohyb vrtule, protože ten při pohonu a za letu každá její část, mimo osy, vykonává.

Vpravo nahoře je graficky znázorněna závislost mezi stoupáním vrtule a jejím rotačním pohybem. Stoupání vrtule H udává dráhu jakou může vrtule urazit za jednu otáčku.

Vlevo nahoře je uveden trojúhelník vektorů rychlostí s nimiž se vrtule během letu potýká. Mezi tětivami profilů listu a vektorem výsledné rychlosti, zde označené W, jakou se pohybují ve vzduchu po šroubovici, je třeba zachovat vhodný úhel náběhu, při němž budou aerodynamické výkony profilu nejlépe využity.

Vlevo dole je pak grafická a početní závislost mezi teoretickou rychlostí letu V, stoupáním vrtule H a jejími otáčkami n během jedné sekundy.

A pak je tu další obrázek s obdobným znázorněním funkce vrtule jako obrázek předchozí, pouze s trochu jiným označením.

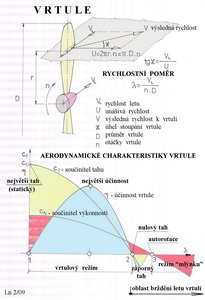
Na každý element vrtule „dotírá“ jiná rychlost obtékajícího vzduchu, zde označená V. Tato rychlost je geometrickým součtem(vzpomeňte na sčítání vektorů, jež jsme již uvedli dříve) rychlosti letu V_L a rychlosti unášivé(rotace) U. Výsledná rychlost svírá s rovinou rotace úhel κ (kapa).

Jestliže uvedeme rotující vrtuli do pohybu můžeme s výhodou popisu jejich vlastností použít poměru rychlosti dopředného pohybu(letu) V_L a součinu otáček a průměru vrtule(ve jmenovateli). Tomuto výrazu se říká rychlostní poměr. Pomocí něho lze popsat pohyb vrtule ve vzduchu.

U vrtule nás zajímá především velikost tahu, který je schopna vyvinout a výkon, který je schopna přenést z motoru na letoun. Obě tyto veličiny vztaženy pomocí součinitele tahu c_T a součinitele výkonnosti c_N ku rychlostnímu poměru λ mají pak stejnou funkci jakou součinitele vztlaku a odporu v závislosti na úhlu náběhu(což již známe).

A teď ke spodní části obrázku. Zde jsou na svislou osu vynášeny součinitele tahu a výkonnosti společně s účinností vrtule. Na ose vodorovné je průběh rychlostního poměru.

V bodě 1 stojí otáčející se vrtule na místě a má největší tah, protože zkroucený list vrtule je ofukován po celé své délce(poloměru) pod velkými úhly náběhu. Pokud jsou takto posuzovány vrtule s většími hodnotami stoupání pak se setkáme s velkým spotřebovávaným výkonem motoru a také často s velkým hlukem způsobeným odtrháváním proudu od listů. Účinnost je rovna nule, přes značný příkon, protože vrtule stojí na místě a nekoná proto svým tahem užitečnou práci. V podstatě nějak dozadu rozhání vzduch.

Jestliže se letoun dá s rotující vrtulí do pohybu dostáváme se do tzv. vrtulového režimu, kdy účinnost celého procesu nejprve rychle stoupá, aby po dosažení svého maxima začala zase klesat. Když i dále zvyšujeme rychlostní poměr λ, k tomu dochází např.při stejných anebo menších otáčkách a snahou o zvýšení rychlosti letu, využitelný tah vrtule se zcela vytratí stejně tak jako účinnost. Pro to, aby se vrtule mohla stále otáčet potřebuje i v tomto režimu nezbytnou výkonnost pro překonání aerodynamických odporů. Je to bod 2 v diagramu.

Naší snahou je proto vždy zvolit pro svůj létající stroj takový rychlostní poměr, aby účinnost vrtule byla co největší. S tím bezprostředně souvisí i volby průměru a úhlů nastavení listů.

Při dalším zvětšování λ se dostáváme s vrtulí do režimu brzdění. Vrtule mezi body 2 a 3 vyvozuje záporný tah (proti směru letu a ten se sčítá s celkovým odporem), i když stále ještě nějakou výkonnost spotřebovává.

Jakoukoliv výkonnost přestane vrtule potřebovat dostane-li se do režimu autorotace, je to bod 3, kdy se samovolně otáčí (pokud jí v tom nebrání nějaké jiné než aerodynamické odpory). Takhle běžně pracují rotory vírníků a také rotory vrtulníků při sestupu bez motoru.

Dalším posunutím na ose rychlostního poměru vpravo se dostane vrtule do tzv. režimu „mlýnku“, kdy sice stále brzdí, ale je již schopna dodávat výkonnost. To je princip využívaný u větrných elektráren nebo možnost pro pokus o znovu spuštění motoru letadla dynamickým účinkem vzduchu při zvýšené rychlosti klouzavého letu.

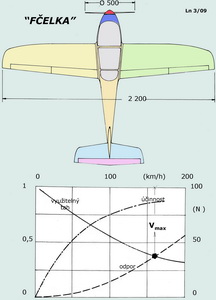
A teď jak to může být se statickým tahem a tahem využitelným? Pokusíme se to ukázat na jakémsi fiktivním příkladu podle předchozího obrázku, který sice nebude úplně kopírovat skutečnost, ale pro náš výklad by měl postačit.

Mějme motor o výkonu 3kW a otáčkách 6 000 1/min opatřený dvoulistou vrtulí o průměru 500mm. Tuto jednotku podrobíme pomocí jednoduchého programu bližšímu posouzení pro různé rychlosti letu a budeme sledovat co se bude dít.

A to až k dosažení maximální vodorovné rychlosti letu, které může, daná pohonná jednotka s letounem o nosné ploše 0,6m² a součinitelem celkového odporu 0,05, dosáhnout.

Zvolme rozsah rychlostí v rozmezí 10 ≤ V ≤ 200 km/h.

V	10	20	40	60	100	150	200	km/h
Tv	?	89,5(?)	79,4	70	54	40,4	31,6	N
η	13,1	24,9	44,1	58,3	75	84	88(?)	%
X	0,15	0,56	2,2	5,1	14,1	32	56	N

Zde jsou použity tyto symboly:

V - rychlost letu

T_V - využitelný tah pro let

η - účinnost vrtule

X - odpor letounu při dané rychlosti.

Když nyní pohlédnete na tabulku můžete konstatovat, že využitelný tah se se zvyšující rychlostí letu zmenšuje. Zde můžeme odhadnout, že statický tah, protože V=0 m/s, použité pohonné jednotky by mohl být asi 100N. Pak ještě zjistíme jak se mění účinnost vrtule s rychlostí letu a extrapolací vypočtených hodnot stanovit, že pro statický test při tahu 100N je účinnost rovna nule. Protože každý výpočtový program má svá omezení pokládejme nejvyšší zde vypočtenou hodnotu účinnosti za málo reálnou.

Nyní neopomeňte zaznamenat jak dramaticky narůstá odpor letounu. Když tedy např. uvážíme, že by se letoun mohl, při přijatelném zatížení nosné plochy, udržet v ovladatelném letu při rychlosti 40km/h, pak jeho odpor vzroste při rychlosti 200km/h na 25-ti násobek. Ale může takové rychlosti s touto pohonnou jednotkou dosáhnout?!

K tomu je třeba porovnat průběhy využitelných tahů pohonné jednotky a odporů letounu v závislosti na rychlostech letu, třeba grafickou metodou. Viz předchozí obrázek. Jejich průsečíku odpovídá na vodorovné ose, kam vynášíme rychlosti letu, hodnota kolem 161km/h.

Předchozích několik odstavců mělo prokázat, že statický tah, jimiž jsou skoro vždy provázeny výkonové údaje vrtulových pohonných jednotek od výrobců, je sice hodnotou zajímavou nikoliv však dostatečně vypovídající pro posuzovaný letoun a její využití v něm.

Tím zatím skončíme toto povídání o vrtulích, aby si mohli dychtiví čtenáři trochu oddychnout a pouze připomeneme:

-protože podmínky proudění nejsou po celé délce listu stejné, je účelné zavést jejich jakousi referenční hodnotu, která je v asi 70 až 75% jeho délky(poloměru vrtule). Pro tato místa by se mělo udávat stoupání vrtule, které je obvykle druhou důležitou geometrickou charakteristikou vrtule po jejím průměru.

Hodnota stoupání vrtule nemusí být, a také skoro nikdy není, stejná po celé délce listu. Souvisí to jednak s okolnostmi výroby a pevností vrtule nebo se záměrnou snahou udržet co nejvyšší hodnoty účinností pevné, za letu nestavitelné vrtule, v širším rozsahu letových rychlostí.