O stabilitě letounů
1. část

Jak již název hlásá bude zde povídání o stabilitě (stabilitách) letounů s pevnými křídly. Něco tak zvaně stabilního jako je například finanční trh, politická či vojenská situace a podobně, v tomto článku zcela opomeneme, protože to není předmětem našeho zájmu, i když se nás to proti naší vůli dost často dotýká zásadně, někdy i fatálně (osudově). Navíc si na to jednak netroufáme a jednak je nám to svou povahou dost cizí, i když je nepřeberné množství těch, kteří se tím z našich peněz dobře živí.

Nám postačí upozornit na to, jak mnohým fatálním následkům při létání předejít a zabránit tak nepříznivým a nebezpečným situacím. Bude k tomu třeba použít populárně srozumitelného výkladu a objasnění některých pojmů, přestože jsme se o nich již dřívě několikrát zmínili. Pokusíme se zahrnout do těchto pojednání i okolnosti ovlivňující vedle skutečných letadel i létající stroje menších rozměrů, tj. modely letadel a případně UAV.

Čím nemůžeme nezačít jsou síly působící na letoun při jeho pohybu vzduchem. Jsou to :

- síly zemské tíže - jejich výslednice působí v těžišti letounu a směřuje do středu Země (svisle dolů). Velikost této výslednice je dána součinem hmotnosti stroje ( v kg) a gravitačním zrychlením (9.81 m/s2) a udáva se v Newtonech (kg.m/s²). Obvykle se předpokládá, že se hmotnost stroje příliš nemění, pokud nedojde ke spotřebě velkého množství paliva nebo po vypuštění břemen apod. Pak je nutno tuto změnu zahrnout do výpočtu.

- síly aerodynamické -jsou síly vzniklé působením okolního prostředí na pohybující se stroj. Ty závisejí na na tvaru letounu, jeho poloze(úhlu náběhu) vůči směru letu, rychlosti letu a na fyzikálních vlastnostech atmosféry Země.

- síly od pohonných jednotek - u proudových nebo raketových motorů je to jejich tah. U pohonných jednotek opatřených vrtulemi vznikají při jejich rotaci vedle tahu i momenty(reakční a gyroskopický).

A pak jsou tu ještě doplňkové síly, které vznikají při křivočarých a nerovnoměrných pohybech letounů. Jedná se hlavně o síly odstředivé a setrvačné.

Pro pohyb letounu platí obvykle pohybové rovnice dle Newtonových zákonů. Pokud se stroj pohybuje rovnoměrně a přímočařě jsou všechny na něj působící síly v rovnováze a jejich součet je nulový. Pokud tomu tak není vzniká za pohybu letounu další doplňková síla. Ten při tom mění buď rychlost nebo se pohybuje po zakřivené dráze nebo koná obojí najednou. Tím se zabývá mechanika letu, která řeší výkony a letové vlastnosti létajících strojů, mezi jinými i stabilitu letu.

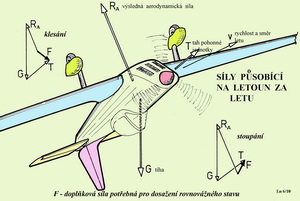
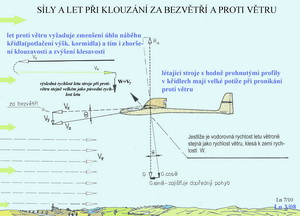
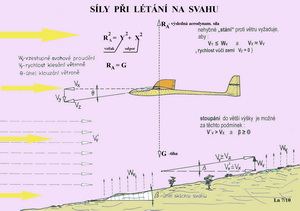
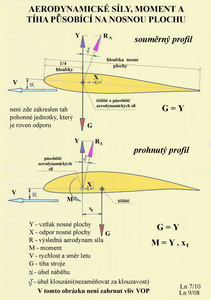
Na tomto obrázku jsou schematicky zachyceny tři hlavní skupiny sil působících na letící stroj.

Z gravitačních sil je to tíha letounu - G.

Ze sil vzniklých vlivem prostředí je to výsledná aerodynamická síla – R_A.

Ze sil od hnací skupiny je to tah – T.

Pak je tu ještě uvedena rychlost a směr letu – V a doplňkové síly – Z, které jsou právě tak velké, aby uzavřely silové obrazce, kdy je dosaženo momentálního rovnovážného stavu.

Vlevo nahoře je to grafický součet vektorů těchto sil – G, R_A, T a F. Doplňková síla F vzniklá změnou tvaru dráhy letu způsobila, že letoun klesá. Aby tomu bylo zabráněno je třeba buď zvětšit výslednou aerodynamickou sílu RA nebo zvětšit tah T nebo obojí.

Vpravo dole je jiný silový diagram, kdy geometrický součet gravitace, výsledné aerodynamické síly a tahu dovoluje letounu stoupat. Jak a kterým směrem ukazuje vektor síly F.

Ve zvláštních případech mohou být uvedené dva případy rovnoměrnými pohyby.

Takhle nějak je možné velmi zjednodušeně popsat okamžitou situaci v pohybu letounu pomocí sil na něj působících.

Vedle sil působí za letu na stroj ještě všeliké momenty, jež mohou jejich příznivé i nepříznivé účinky zesilovat či potlačovat.

Ještě jedno malé odbočení a zpřesnění. Profil, jak známo, je uzavřená rovinná křivka nějakého vhodného tvaru. Takováto křivka není dost dobře schopna vykazovat ani vztlak, odpor a ani moment. Nebo snad ano?

Ne, jistě, že ne. Předpokládá se sice, že kolem ní může vzniknout dvourozměrné proudění-nahoru, dolů, dopředu i dozadu, ale nějaká síla stěží. Proto je profil nahražován křídlem nekonečného rozpětí (nemá žádný okraj) u něhož je zajištěno také pouze dvourozměrné proudění. Takže : profil ≡ křídlo nekonečného rozpětí. a na tom již vznikají aerodynamické síly i momenty, které nás v povídání o stabilitě zajímají. ( To jsme již dříve v jednom z čísel našeho magazínu vysvětlovali nebo je to ve Sborníku vybraných výrazů).

Jak to asi je se vztlakem, který chceme, aby byl vždy co největší, protože víme, že poměr vztlaku ku odporu udává základní aerodynamickou charakteristiku – aerodynamickou jemnost (jejíž převrácená hodnota je nazývána klouzavostí).

Ktomu je vhodné nalistovat Slovník vybraných výrazů (třeba v minulém magazínu) a pod písmenem B si zopakovat o čem napovídá Bernoulliho rovnice. Je to v podstatě zákon o zachování energie platný dost dobře pro nestlačitelné tekutiny, tedy i pro vzduch, až do rychlostí kolem 100 m/s.

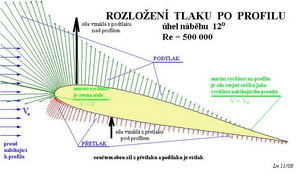
Při pohybu křídla nekonečného rozpětí vzduchem vzniknou kolem něho na horní a dolní straně různé rychlosti (nahoře vyšší než než dole – viz Slovník vybraných pojmů písmeno C – cirkulace) proudění. Jak se snaží ukázat předchozí obrázek. Pokud je místní rychlost proudění na profilu vyšší než rychlost pohybu křídla poklesne v tomto místě tlak v proudu (horní strana profilu) a pokud je zase místní rychlost nižší tlak v proudu stoupne. Délky a směry šipek v obrázku naznačují velikost a směr působení takto vzniklých tlakových sil. Přetlak pod křídlem a podtlak nad křídlem vytvářejí společně výslednou sílu – vztlak, působící v tomto případě směrem vzhůru.

Víme z dřívějška, že aerodynamický střed profilu se nachází, v rozmezí úhlů náběhu mezi cca – 10 a + 15 stupni, velmi přibližně v jedné čtvrtině jeho hloubky. V následujícím obrázku jsou některé výsledky měření NACA ze 40. let minulého století, které se toho týkají.

Poloha těžiště může být naproti tomu zase celkem libovolná. Ne však neomezeně, pokud chceme dosáhnout na létání a nikoliv jen na obecné v podstatě neovladatelné pohybování se vzduchem, coby hmotné těleso.

Použijme jeden z možných příkladů.

Jestliže je těžiště blízko aerodynamického středu nebo je s ním dokonce totožné, může dojít k rovnovážnému letu takto seřízeného křídla, aniž by byla vyžadována jakákoliv jiná stabilizační plocha. Podmínkou k tomu nutnou je však souměrný tvar profilu nebo profil s dvojitým prohnutím. Prostě profily s velmi malým nebo žádným klopným momentem v rozmezí úhlů náběhu mezi -10 a + 12 stupni. Když se k tomu přidá ještě například půdorys nosné plochy tvarovaný do mírného kladného šípu je rovnoměrného přímočarého letu dosaženo. Nemusí to však být podmínka bezpodmínečně splněná. Připomeňme „samokřídla“ typu „rovné prkno“. Z nich jsme vám například přiblížili před časem slavný americký UAV „Helios“ i jeho předchůdce. U nich však bylo použito k řízení také vektorování tahů elektrických pohonných jednotek. a to jak podél příčné tak i podél svislé osy letounu.

V jiných případech, a těch je zatím většina, je však stabilizační plocha, ať již vodorovná ocasní plocha nebo plocha kachní, nezbytně potřebná.

Zopakujme ještě zjednodušeně jaké síly působí v některých letových situacích.

Všímáme si hlavně působení sil ve svislé rovině a jejich změn, protože ty mají zásadní vliv na zachování či obnovu původního letového režimu a tak ovlivňují podélnou stabilitu letounu podstatně.

Tíhu letounu předpokládáme během letu za neměnnou. Výslednou aerodynamickou sílu R_A umísťujeme na stejnou svislici stejně tak jako tíhu G s působištěm v těžišti. Klopný moment vyskytující se především u jednoduše prohnutých profilů zde zatím neuvádíme. Je to všechno oproti skutečnosti poněkud zjednodušené.

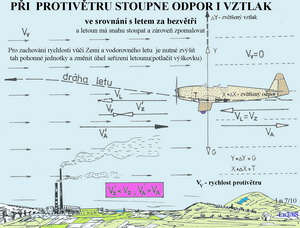
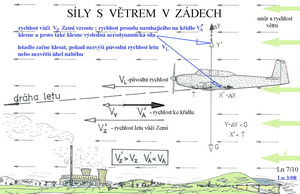
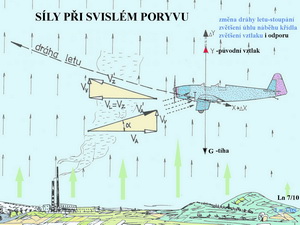
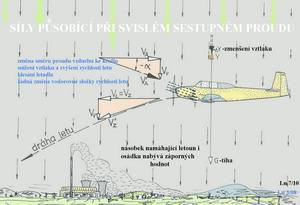
Z předchozích obrázků můžete získat docela dobrou orientaci v tom jak se mohou měnit aerodynamické síly, jestliže dojde k porušení rovnovážného letu vlivem vnějších atmosférických podnětů. Zásahy pilota následují až potom.

Teď již ale nemůžeme beztrestně opomíjet klopný moment provázející všechny jednoduše prohnuté profily. V dalším obrázku jsou dvě schemata působení aerodynamických sil a sil tíže v rovnovážném letu a sice pro profil souměrný(nahoře) a pro profil prohnutý(dole).

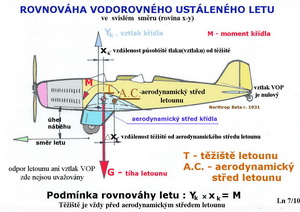
V čem se liší tyto dva případy?

U profilu souměrného je těžiště letounu při rovnoměrném vodorovném přímočarém letu velmi blízko aerodynamickému středu nebo je s ním totožné.

Kdežto u profilu prohnutého, kde již působí klopný moment M, je těžiště letounu za aerodynamickým středem nosné plochy (¼ hloubky střední aerodynamické tětivy). Ne však za aerodynamickým středem letounu.

Tím je, ve vodorovném přímém ustáleném letu, vlivem účinku dvojice sil Y(vztlak) a G(tíha) kompezován účinek klopného momentu, takže nedochází ke klopení(otáčení podle příčné osy letounu). Všimněte si, že vztlak VOP je nulový(tak by to obvykle mělo být při navrhování letounů, protože přídavný odpor VOP je nejmenší).

Ale kam umístit těžiště letounu, aby takový let byl zajištěn???

Položme takovouto otázku: je aerodynamické centrum nosné plochy ve stejném místě jako aerodynamické centrum letounu?

Málokdy. Může znít lakonická, ale ne vše vyčerpávající odpověď.

Podívejte se na následující obrázek, který již znáte z dřívějška.

Z něho je patrné, že aerodynamické centrum nosné plochy je asi ve ¼ její střední aerodynamické tětivy(to již víme z dřívějška). Zde působí její odpor a  vztlak jejichž součtem je výsledná aerodynamická síla.

Za ním se v určité vzdálenosti nachází těžiště letounu, jehož polohu ovlivňuje VOP zásadním způsobem. V případě, že klopný moment nosné plochy působí v uvedeném smyslu, je jeho vzdálenost od ¼ bodu střední aerodynamické tětivy křídla přímo úměrná velikosti klopného momentu.

Když bude klopný moment nulový bude se nacházet těžiště letounu velmi přibližně v ¼ střední aerodynamické tětivy.

Jestliže ale bude mít klopný moment opačný smysl působení je nutné posunout těžiště letounu před ¼ hloubky střední aerodynamické tětivy.

A tady skončíme s 1. částí o stabilitě letounů malých i „dospělých“.