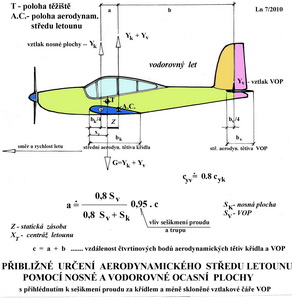
O stabilitě letounů
2. část

Opatrné opakování:

- aerodynamické centrum letounu (A.C.) je místo k němuž je výsledný součinitel jeho klopného momentu stálý, bez ohledu na úhel náběhu, který právě letoun vůči směru letu zaujímá

- těžiště letounu je místo do něhož soustřeďujeme jeho celkovou hmotnost, která zde pak působí jako tíha, to jest síla působící do středu Země a udává se ve fyzikálních jednotkách zvaných Newtony s rozměrem [kg.m/s²].

O vzájemné poloze těchto míst(bodů) na letounu jsme pohovořili již v minulém článku. A pokusili jsme se stručně popsat jaký vliv to má na podélnou stabilitu letounu(modelu).

Polohu těžiště létajícího stroje jsme schopni určit dostatečně přesně. Buď výpočtem nebo vážením.

Co ale s polohou jeho aerodynamického středu? Kde se nachází? Můžeme postupovat například takto:

Vycházíme ze známé polohy aerodynamického středu nosné plochy, která se nachází cca ve 25% její střední aerodynamické hloubky.

Jestliže k nosné ploše přiřadíme další části letounu – trup, motorové gondoly, podvozek,... posune se jeho A.C. mírně dopředu. Tento posun je tím větší čím jsou tyto části objemnější.

Když však ale přiřadíme k nosné ploše ještě VOP – vodorovnou ocasní plochu(nepleťte si ji s výškovkou, protože to je jen její pohyblivá část) posune se A.C. letounu dozadu od její náběžné hrany. Lépe řečeno od jejího A.C.

Ale kam?!?!

To se teď pokusíme vysvětlit pomocí následujícího obrázku.

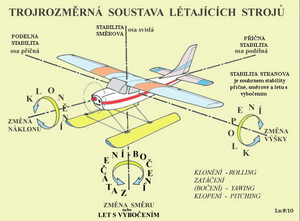
Co na něm je?

Je toho dost, ale ne zase tolik, aby gramotní čtenáři našeho časopisu nepochopili obsah tohoto sdělení.

Je to grafické vyjádření vlivu velikosti a polohy VOP na polohu A.C. letounu. To má významný vliv na posun A.C. směrem dozadu od ¼ bodu střední aerodynamické tětivy nosné plochy.

A jak to tedy funguje?

Jestliže dojde během letu ke zvětšení úhlu náběhu letounu vznikne na VOP vztlak, který na příslušném rameni ( v předchozím obrázku c = a + b) vyvolá výrazný klopný moment ve smyslu „na hlavu“, jež se snaží obnovit původní úhel náběhu. Tedy moment stabilizující.

To nám vyhovuje a jsme tomu rádi.

Tento příznivý účinek VOP je ještě větší, když VOP není umístěna za nosnou plochou v oblasti sešikmení proudu. Oč běží jsme si vysvětlili dříve.

Při náhlém zvětšení úhlu náběhu letu vzroste vztlak VOP méně než je tomu u nosné plochy, protože zvětšení úhlu náběhu VOP je ve srovnání s ní menší. Je nutné počítat počítat s vlivem obvykle menší štíhlosti a také menšího Re čísla u ní.

To se týká zejména modelů letadel a UAV. Proto je také sklon vztlakové čáry VOP menší než u nosné plochy a s tím je nutné také při posuzování polohy A.C. letounu počítat.

Takže jestliže známe velikost nosné plochy, velikost VOP a jejich vzájemnou polohu můžeme, při prve uvedených předpokladech, stanovit přibližnou polohu A.C. letounu podle vztahu uvedeného v předchozím obrázku. Tak se dostáváme k významnému údaji, po kterém jsme se pídili a toužili.

Teď ho máme a víme kam až můžeme posouvat polohu těžiště, aniž bychom způsobili letoun méně nebo vůbec ovladatelným. Pro první a hrubé posouzení stavu vzájemného postavení těžiště a A.C. to celkem vyhovuje, i když jsou samozřejmě k dispozici přesnější, ale zároven složitější postupy.

Dosadit do jednoduchého matematického vztahu v předchozím obrázku a vypočítat z něj přibližnou polohu A.C. by mělo činit potíže snad málokomu.

Ukažme to na třech příkladech, jestliže přijmeme uvedené opravné součinitelé za přijatelné:

a) Pro S_V = S_K bude poloha A.C. přibližně ve vzdálenosti 0,444c. Je to případ tandémového uspořádání nosných ploch.

b) Pro S_V = 0 bude přibližná poloha A.C. nejdále ve 25% střední aerodynamické hloubky. To jsou případy samokřídel.

c) Pro S_V = 0,1 S_K bude přibližná poloha A.C. letounu ve 0,075c.

c – vzdálenost A.C nosné plochy od A.C. VOP

Když bychom připustili ještě další prakticky ověřené zvyklosti z navrhování letounů související se vzdálenostmi ¼ bodů nosné a vodorovné ocasní plochy ( v obrázku označeno jako c), jakožto násobek střední aerodynamické hloubky nosné plochy (bk), tak například pro c = 5b_k bude přibližná poloha A.C. pro předchozí příklad c) v 37% b_k.

Obdobně pro c = 4b_k bude přibližná poloha A.C. v cca 30% b_k.

Takže teď když máme představu o poloze A.C. letounu můžeme pokračovat v úvahách například o jeho podélné stabilitě.

Nejdříve však bude vhodné naznačit o čem může být v pojednání o stabilitě řeč. Není toho málo a není to nepodstatné.

Nebudeme zde rozebírat podrobně výrazy statická a dynamická stabilita. To ponechme do vysokoškolských skript.

Bude však účelné, když rozdělíme celkovou stabilitu letounu do několika skupin ovlivňujících jeho letové vlastnosti. Můžeme tedy posuzovat letové vlastnosti v podélném pohybu (podél osy příčné), v pohybu směrovém (podél osy svislé), v pohybech příčných (kolem osy podélné) a konečně v pohybech stranových (současně podél osy podélné a svislé).

V dalším obrázku je připometa nám již známá trojrozměrná aerodynamická soustava se systémem tří os(pohybujeme se v trojrozměrném prostoru) , tomu odpovídajících tří hlavních pohybů každého letounu, s nimi spojených druhů stabilit a poznámka o stabilitě stranové.

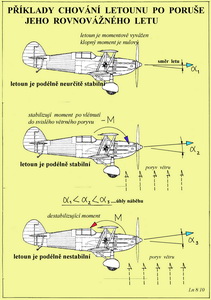
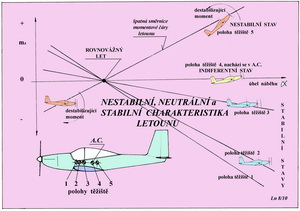
Takže ještě jednou obecný úvod: každý letoun může být dostatečně, málo, vhodně nebo vůbec ne stabilní.

Dostatečnou mírou stability rozumíme zřetelnou snahu létajícího stroje navracet se po poruše letu do původního letového stavu, automaticky. To jest pomocí jeho vlastních letových vlastností. Zásah pilota do řízení není vždy ihned nezbytně nutný.

Malou mírou stability rozumíme totéž jako prve, ale s mnohem menší ochotou a rychlostí. Zásah pilota je obvykle, po poruše jakéhokoliv letového stavu, velmi rychle potřebný.

Vhodnou mírou stability míníme pak právě takové nezáludné letové vlastnosti, které při zachování její přiměřené míry umožní zaujímat zvolené letové stavy snadno a rychle. Zásah pilota je vždy nutný s malým časovým předstihem nebo nejpozději v okamžiku, kdy má dojít ke změně letového stavu.Tím máme na mysli letouny určené především pro akrobatické poletování s dostatečně vyspělým pilotem.

Za nedostatečnou míru stability( tedy za nestabilitu) považujeme takové letové vlastnosti, kdy je velmi náročné a mnohdy i nemožné dosáhnout plně ovladatený let. Zásah pilota se již míjí potřebným účinkem a dokonce může vzniklou nestabilní situaci ještě zhoršit.

I když jsou všechny zde dříve uvedené druhy stabilit důležité pro spolehlivé létání, je přece jenom vhodné vytvořit jakési pořadí jejich důležitosti pro leteckou praxi, jakkoliv se názory na to mohou dost lišit.

Začněme tedy se stabilitou podélnou, která souvisí s pohyby letounu kolem jeho příčné osy (viz předchozí obrázek). Zde mají rozhodující význam klopné momenty vzhledem k těžišti, které určují do jakého úhlu náběhu se letoun nastaví během letu. Protože již víme, že úhel náběhu má zásadní vliv na velikost výsledné aerodynamické síly a klopného momentu, tak tento poznatek akceptujeme. K bližšímu objasnění těchto stavů použijeme následující obrázek.

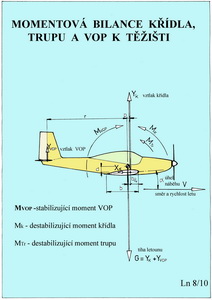
V horní části obrázku je pokus znázornit letový stav AVIE jakožto momentově vyvážený. Výsledný moment letounu k těžišti je nulový a ten se pohybuje rovnovážným ustáleným letem.

Ale jen tak dlouho dokud nedojde k nějakému vnějšímu podnětu, například při vlétnutí do svislého větrného poryvu. To je znázorněno uprostřed obrázku.

Letoun okamžitě zvětší úhel náběhu svého pohybu a má snahu stoupat a zpomalovat let. To je obvykle nejen nežádoucí, ale i nebezpečné. Jestliže za této situace vznikne na letounu klopný moment ( zde se znaménkem minus – těžký na hlavu) snažící se ho navrátit do původního letového stavu pokládáme letoun s takovouto vlastností za stabilní. Poloha těžiště je vždy před A.C. ( ve směru letu).

Když však takovýto klopný moment nevznikne, bude mít letoun snahu se pohybovat v novém letovém režimu nastálém po vnější poruše. Nebude tedy ani stabilní ani nestabilní. Toto jeho indiferentní chování může však být akceptováno jen ve zvláštních případech, kdy toužíme po velmi „mrštném“ stroji a k jeho pilotování se podvolí patřičný odvážlivec. U tohoto letounu, ve srovnání s předchozím „hodným“ strojem, budou polohy těžiště a A.C. velmi blízké a nepřesáhnou zřejmě 0,5% střední aerodynamické hloubky jeho nosné plochy.

Pokud, ale vznikne na letounu za prve zmíněné situace vlivem vnějšího podnětu, klopný moment (zde se znaménkem plus) snažící se vzniklý nárůst úhlu náběhu dále zvětšovat, takže o návratu do původního stavu nemůže být ani zmínky, pak je takovýto letoun nestabilní. To je zachyceno ve spodní části předchozího obrázku. Příčin může být více. Jednou z nich je typický případ, kdy je těžiště letounu za jeho A.C.

Tak a teď, protože to není jen tak ledajaké povídání, to popíšeme ještě trochu jinak. Popis předchozího obrázku by mohl totiž někoho uvést do několika nejasností.

Stále se tady mluví o tom jestli vznikne nebo nevznikne stabilizující moment snažící se uvést letoun do letové polohy před porušením rovnovážného letu, třeba tím, že vletěl do vzestupného proudu.

Nebo, že žádný nevznikne a letoun pokračuje, ale ne moc dlouho, v poloze do níž byl uveden vnějším vlivem.

A také se tady vyhrožuje tím, že když je vzájemná poloha těžiště a A.C. letounu nevhodná, tak letoun po vlétnutí do svislého proudu vzduchu s následnou změnou úhlu náběhu se ho nejen nesnaží uvést do původního stavu, ale ještě ho začne zvětšovat.

Vezměme na pomoc následující obrázek, kde jsou uvedeny případy působení třech důležitých částí letounu. Z hlediska výkonů již víme, že to je hlavně nosná plocha, která je ovlivňuje, ale teď nemluvíme o výkonech. Abychom jich dosáhli musíme mít letoun ještě s nezbytnými letovými vlastnostmi. A jednou z nich, jak jsme již připomínali dříve je stabilita.

Takže za těchto okolností není nejdůležitější pro dosažení potřebné míry stability nosná plocha (křídlo), ale je to VOP (vodorovná ocasní plocha) jinak zvaná též stabilizátor ( nikoliv však výškovka, jak stále mnozí používají). A proč tomu tak je může pro čtenáře našeho magazínu být patrné, jasné a pochopitelné z toho následujícího obrázku.

Bez sáhodlouhých dokazování vezměte za ověřené, že ani samotná nosná plocha ani samotný trup (ten už vůbec ne, chová se za letu dost podobně jako hozený oštěp) nepůsobí svými účinky příznivě k nápravě poruchy letové dráhy.

Ale ani samotná VOP, o níž je zde také řeč, nepůsobí v tomto případě nijak významně. Jenže v součinnosti s ramenem na němž vůči těžišti působí, zde označeném jako r, vytváří velmi příznivě působící moment - MVOP, který může být řešením pro nápravu porušené dráhy letu.

Z obrázku lze poznat, že klopný moment VOP má opačný smysl působení než destabilizující klopivé momenty křídla a trupu.

Chceme-li tedy využít přízivého působení klopného momentu VOP ke stabilizaci letu v podélném směru, musíme ji umístit do vhodné vzdálenosti za nosnou plochou a vybavit ji potřebnou velikostí. Poměříme-li její plošnou velikost s nosnou plochou a rameno na němž působí se střední aerodynamickou tětivou nosné plochy, získáváme bezrozměrný údaj zvaný mohutnost VOP. Tato veličina je při navrhování letounů běžně používána.

Ještě k předchozímu obrázku několik souvětí.

Není zde zachycen klopný moment nosné plochy, který jak již vícekrát víme, má u prohnutých profilů smysl shodný s během hodinových ručiček. Tedy – „těžký na hlavu“.

Jestliže by se letoun pohyboval rovnoměrným přímočarým letem a v rovnováze by byl moment vyvozený vztlakem křídla k těžišti s klopným momentem nosné plochy, pak by VOP nemusela vykazovat žádný vztlak. To již jsme dříve popisovali.

Po vlétnutí do svislého poryvu a následným zvětšením úhlů náběhu na křídle i VOP, má vytvořit VOP klopný stabilizující moment, který by měl přemoci nepříznivé účinky destabilizujících momentů samotné nosné plochy a trupu(včetně podvozku a případných motorových gondol). Když to takový letoun dokáže v době nepřevyšující pouze několik málo sekund je to vhodný stroj pro bezpečný a spolehlivý provoz.

Jestliže si ale bude počínat liknavě, nemůže být svěřen do rukou nezkušených ani pilotů ani modelářů, pokud se ovšem nebude jednat o záměrné ovlivnění řiditelnosti například u akrobatických letounů pro zvýšení adrenalinu v krevním oběhu nebo pro pobavení diváků či zapůsobení na hodnotící porotu.

Když ale dokonce nebude letoun poslušný výchylek výškového kormidla, jakkoliv směřujících k získání stabilizujícího momentu, k nápravě hrozivého stavu, pak nelze obvykle očekávat hladké přistání.

A nyní ještě jednou ukročíme poněkud stranou a podíváme se na podélnou stabilitu odjinud. Na dalším obrázku je diagram na jehož svislou osu je vynášen součinitel celkového klopného momentu letounu – m_z a na osu vodorovnou úhel náběhu letounu - α.

Z něj můžete pochytit, že součinitel klopného momentu samotného trupu se se zvětšujícím se úhlem náběhu posouvá k větším hodnotám. A to nad osou úhlů náběhu vpravo a vychyluje ho stále do méně a méně stabilní polohy. Místo, aby úhel náběhu nyní zmenšoval tak ho stále zvětšuje. Pod osou úhlů náběhu začíná působit klopný moment opačného smyslu a poloha samotného trupu je destabilizována více a více, i když na opačnou stranu. Místo, aby teď úhel náběhu zvětšoval, tak ho zmenšuje.

Pro samotné křídlo je průběh obdobný. Křídlo při pohybu od nulového součinitele klopného momentu k jeho větším hodnotám ( v diagramu směrem doprava), nabývá stále větší snahu tento úhel zvětšovat. Od téhož místa (v diagramu směrem doleva) má sice zase snahu klopný moment zmenšovat, ale smysl působení je opačný . Obojí vede k větší a větší snaze pohyb destabilizovat.

Nyní upozornění: při všech dosavadních úvahách zapomeňte zatím na A.C. letounu. To nás teď příliš nezajímá. Pro naše úvahy je teď důležitá poloha těžiště a proto je klopný moment letounu, zde zmiňovaný, vztahovaný k jeho těžišti.

Zásadní význam pro míru stability při těchto úvahách má VOP, respektive klopný moment, který vyvozuje k těžišti. Proto se také mnohdy VOP nazývá stabilizátorem.

Co je ze stále stejného diagramu zcela zřetelné je to, že momentová čára VOP má opačnou směrnici (sklon) než samotný trup nebo samotné křídlo. Takže v části diagramu nad osou úhlů náběhu se kladný klopný moment VOP se zvětšujícím se úhlem náběhu sice zmenšuje ale při tom působí příznivě směrem k obnově původního stavu letu.

Pod osou úhlů náběhu se klopný moment zvětšuje, ale má opačný smysl než prve. Náhle zmenšený úhel náběhu se tak snaží zvětšovat, aby bylo dosaženo jeho původní hodnoty, která je v průsečíku momentové čáry (přímky) s vodorovnou osou.

Obojí má za následek snahu obnovit původní letový stav. VOP na vhodném rameni tedy působí z hlediska stability nesmírně příznivě.

A nakonec je tu křivka(přímka) poslední a ta platí pro kompletní letoun - trup, křídlo i VOP. Její sklon je o něco menší než sklon VOP, ale účinky na podélnou stabilitu letounu jsou obdobné. Protíná osu úhlů náběhu v místě, kde se nachází rovnovážný stav letu letounu.

Pokud se týče klopných momentů trupu, křídla a VOP je nutné je pro zhodnocení podélné stability letounu vždy spočítat. Jiná cesta, vyjma snad nákladných měření v tunelu, není. My jsme se těmto výpočtům zde vyhnuli, abychom naše některé čtenáře nevyděsili, i když to nejsou počty zas tak obtížné a po sestavení jednoduchého programu snadno a rychle uskutečnitelné.

Teď si dovolíme předvést na stejném typu diagramu jako prve, jak to asi dopadne jestliže se domůžeme prve zmíněných hodnot klopných momentů k těžišti v závislosti na úhlech náběhu letu pro několik případů stabilitních stavů letounu.

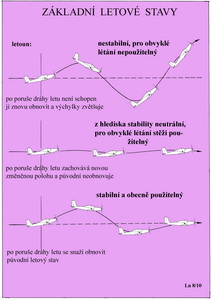
Osa svislá i vodorovná náležejí stejným parametrům jako prve, jedná se však o kompletní letoun a jeho momentové křivky v závislosti na poloze jeho těžiště vůči A.C.

Všechny momentové přímky letounu se protínají v jednom bodě na ose úhlů náběhu, který přísluší jeho rovnovážnému letu.

Začněme odzadu od číslice 5. Těžiště letounu je v této poloze za jeho A.C. a tomu také odpovídá průběh momentové křivky. Směrem odleva doprava stoupá a  popisuje velmi neutěšený nestabilní stav letounu. Mohutnost VOP nestačí na to, aby změnila tuto nepříznivou stabilitní charakteristiku letounu vzhledem k přílišné zadní poloza těžiště – až za A.C. Letoun je pro obvykle létání nejen nepoužitelný, ale i nebezpečný pro osádku i okolí.

Protože jsme již poučeni předchozími povídáními dovolujeme si posunout těžiště letounu kupředu, směrem k náběžné hraně střední hloubky jeho nosné plochy. Tentokrát právě do místa kde se nachází jeho A.C, to jest poloha označení číslicí 4. A co po výpočtech zjistíme je, že letoun je sice schopen letu, ale pilotovi (modeláři) jeho úlohu v řízení nijak neusnadňuje, protože kam se naklopí, ale i nakloní, tam jeho poloha setrvá tak dlouho dokud nepřijde nějaký vnější podnět nebo zásah pilota. Změny polohy jsou velmi prudké a velké. Pro obvyklé létání, kupříkladu propagované létání pro radost od LAA ČR, nedoporučený stav.

Pak se dostáváme do polohy težiště označené číslicí 3. Ta je zjevně před polohou A.C. a ejhle, letounova momentová křivka je již příznivá. Letové vlastnosti takovéhoto letounu jsou již prakticky použitelné a závisí jen na jeho provozovateli jak daleko před A.C. nebo jak blízko k němu těžiště umístí.

A nakonec jsou tu dvě další číslice 2 a 1, označující polohy těžiště ještě blíže náběžné hraně křídla než prve. Momentové křivky takového letounu mají ještě strmější sestup než ta předchozí a oznamují, že podélné stability je dost a dost. Jenže v případě 1 až příliš, což se nepříznivě projeví na letových vlastnostech i výkonech. Letoun se sice pohybje vzduchem, ale jeho pohyb je těžkopádný a nemotorný. V podstatě „rozhrnuje“ vzduch víc než je třeba. Někdy není sice jiného řešení, ale nic se nemá přehánět.

Snad by stálo za to zapamovat si, že pokud budete moci nahlédnout na momentovou křivku letounu, nebo si ji sami spočítáte, měla by směřovat u našeho typu diagramu vždy shora zleva vpravo dolů. Čím více bude skloněna dolů tím vyšší míru podélné stability lze očekávat, což byl náš cíl.

A aby to nebylo jen stále takové bloumání po diagramech je v dalším obrázku schema velmi pravděpodobných pohybů letounu, jestliže je jeho stabilita nedostatečná (nahoře) nebo neutrální (uprostřed) a nebo dostatečná (dole) a pro létání vhodná.

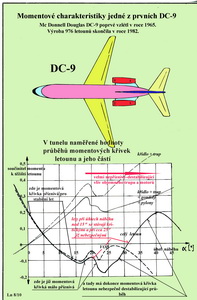
A nakonec je tu ještě jeden diagram pro orientaci v tom jak to asi mohlo vypadat s počátečními návrhy legendární DC-9 pokud se týče jejich stabilitních charakteristik naměřených před cca 50 lety v aerodynamickém tunelu. Jestli jsou ty údaje pravdivé, tak to byl při trochu větších úhlech náběhu dost vrtošivý eroplán. Podívejte se na následující obrázek.

A pro ty, kdo snad již nevědí jak stroj od Mc Donnell Douglasů z počátku 60. let 20. století vypadal, přidáváme jednu fotografii.

Tady povídání o podélné stabilitě, pro tentokrát, končí. Snad vás ten článek příliš neunavil nebo od létání neodradil.