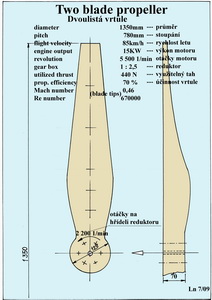
Dotaz na závislost mezi průměrem vrtule a účinností

Dostal jsem dotaz od čtenáře V.K.našeho magazínu, který se s důvěrou obrátil na nás kvůli případnému vysvětlení toho jak to je nebo může být s účinností vrtule, když se začne měnit její průměr.

Na to se dá odpovědět rychle a stručně asi následovně: účinnost vrtule obecně roste se zvětšujícím se průměrem vrtule. Ale jen do určité míry. Pak začíná klesat. A navíc během rostoucího průměru, pokud zachováváme stejné otáčky, hlučí čím dál víc, až to může být nesnesitelné.

Abychom však rozšířili smysluplné informace, tak jak se o to snažíme v našem magazínu neustále, dokážeme to na následujícím příkladu. Ten je sice poněkud scholastický(zkostnatělý), ale jinak se nemůžeme dobrat nějakého gramotného výsledku.

Pro tento příklad je nutné učinit jisté předpoklady, které zůstanou pro posouzení závislosti účinnosti na více průměrech, stálé. Použil jsem následujících vstupních podmínek:

• výkon na hřídeli vrtule je 10 kW
• otáčky mají hodnotu 2 600 ot./min
• předpokládaná rychlost letu 100 km/h
• počet listů vrtule 2

Když jsem tyto údaje podrobil pro šest průměrů vrtule početní analýze dostal jsem údaje z nichž jsem vybral – účinnost, využitelný tah, a Machovo číslo konců listů. Vypadá to následovně, když připustíme, že by profil listů mohl mít tloušťku kolem 11,5% a prohnutí cca 3,5% a jeho úhel náběhu asi 3,5 stupně:

průměr D	účinnost	využitelný tah	Machovo číslo
mm	%	N	-
500	48	173	0,22
750	67	241	0,31
1 000	74	265	0,41
1 500	77	276	0,61
1 750	77	276	0,71
1 900	76	274	0,76

Z tabulky je na první pohled patrné, že nejvyšší účinností dosahuje za výše uvedených poměrů vrtule s průměrem asi 1 700 mm. Ta poskytuje také největší hodnotu využitelného tahu cca 277 N.

Pokud byste měli přístup k ostatním výsledkům výpočtů zjistili byste, že úhly nastavení listů se sice například v 70% průměru liší, ale výsledný údaj o postupu vrtule za jednu otáčku ve směru letu (to se nazývá stoupáním vrtule ) je stejný a v tomto případě asi 950 mm.

Povšimněte si také jak asi narůstá hluk vrtule s jejím zvětšovaným průměrem. Ten častokrát převýší svojí intezitou hluk spalovacího motoru.

Takže ledaskoho napadně, že by bylo záhodno snížit otáčky, dejme tomu na hodnotu 2 200 1/min. A jak to asi teď dopadne pro vrtuli s průměrem 1 700 mm, která vyšla prve jako nejlepší?

Znovu ….....10 kW ; 100 km/h ; 2 listy :

1 700 mm ; účinnost 78,5% ; využitelný tah 282 N ; Machovo č. 0,58

A ejhle, vesměs příznivější výsledky. I když ne nijak převratné, ale lepší než v kterémkoliv dřívějším případě.

Tuto okolnost nebudeme nijak podrobně vysvětlovat, protože každému napoví, že každý letoun by měl mít pro sebe navrženou vrtuli s nejlepší účinností proto, aby spotřeboval co nejméně paliva a vytvářel nejméně hluku. Tuto činnost lze nazvat například optimalizací výběru vrtule pro letoun s daným pohonným soustrojím(motorem).

Nějakou dobu to samozřejmě trvá, ale vyplatí se to vždy. Ať se jedná o vrtule pevné nebo stavitelné. Uvedl jsem to jako logický další krok při návrhu vhodné vrtule.

Souvisí s tím samozřejmě ještě výběr vhodného profilu, návrh tvaru listů a jejich počet.

V předchozím obrázku je příklad vrtule pro menší lehký letoun.

A ještě jedno upozornění nakonec. Není dost dobře možné, pokud se chcete dobrat správného výsledku, posuzovat účinnost pohonné jednotky( motoru + reduktor + vrtule) s účinností samotné vrtule. Tento nesprávný postup může být mnohými přehlížen a z toho plynoucí závěry špatně použitelné.

Oč asi běží jsme již připomínali v některém z dřívějších čísel Akademie. Připomenu to ještě jednou: celková účinnost pohonné jednotky není dána prostým součtem účinností jeho částí, ale je dána jejich součinem.

Takže je-li například účinnost motoru, tj. poměr mezi množstvím vstupní energie( volty x ampéry) a energií výstupní (na výstupním hřídeli motoru) 75%, účinnost reduktoru asi 98% a účinnost samotné vrtule 75%, je výsledná účinnost pohonné jednotky :

(0,75 x 0,98 x 0,75) x 100 = 55,1%

Když bude použita jiná pohonná jednotka, v níž její jednotlivé části budou mít jiné účinnosti, ačkoliv množství vstupní energie bude stejné jako prve, tak s lepším motorem(účinnost 80%) i trochu lepší vrtulí(účinnost 78%) bude výsledná účinnost pohonné jednotky

(0,80 x 0,98 x 0,78) x 100 = 61,2%

Tato pohonná jednotka využije stejné množství energie přibližně

61,2/55,1 = 1,11 krát lépe.

To znamená, že například stroj s touto jednotkou a stejným množstvím „paliva“ doletí o 11% dále. Účinnost vrtule při tom stoupla ale jen o 3%.

Asi takhle by měly být posuzovány výkony vrtulových pohonných jednotek. Vrtuli je pak třeba navrhnout a dimenzovat vždy tak, aby výkon na hřídeli motoru(reduktoru), který přebírá přeměnila ve využitelný výkon co nejúčinněji.