Aerodynamická tětiva

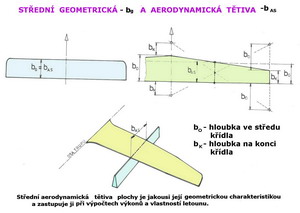
Co to je? Zase nějaká smyšlenka těch co si myslí, že teorie je to pravé? Nebo jedno jejich zaklínadlo, aby se mohli vyvyšovat nad obecnými, k létajícím strojům, lnoucími lidmi, ať již malými či dospělými? Není to nějaká nadávka či dvojsmyslný jinotaj? K čemu to vlastně je? Je to vůbec k něčemu?

Ku příkladu křídlo je pro každého celkem pochopitelný pojem, protože je možné ho nakreslit, vyrobit i rozbít. Střední aerodynamickou tětivu, jakkoliv je spjata s nějakou nosnou nebo ocasní plochou, jako jejich důležitá geometrická charakteristika, je možné jen spočítat či nakreslit. Proto je abstraktním pojmem k němuž je nutno vytvářet obezřetný, ale spíše odmítavý vztah, míní mnozí. Při zvažování výhod či nevýhod toho kterého návrhu létacího stroje ji však nelze opomenout.

Pokusím se vysvětlit o co asi jde.

U letadel s pevnými i pohyblivými křídly(vrtulníky, vírníky) mají značnou důležitost, mimo jiné, nosné a ocasní plochy. Každá z nich má nějaký tvar a velikost. Nejjednodušším půdorysným tvarem je obdélník u něhož je po celém rozpětí zachována stejná hloubka. Viz tvar vlevo v připojeném obrázku.

U složitějších tvarů ploch je nezřídka používaná v předběžných rozvahách o výkonech náhradní obdélníková plocha s tak zvanou střední geometrickou hloubkou - viz náčrt vpravo v připojeném obrázku. Je to plocha o původním rozpětí se stálou hloubkou b_G, které spolu vytvářejí obdélníkovou plochu původní velikosti. Tak se rychle může stanovit například štíhlost křídla, což je údaj důležitý pro další rozhodování.

Pak z předpokládané letové hmotnosti letounu určíme zatížení nosné plochy. Z ní dále rychlost letu pro zvolený rozsah součinitelů vztlaku a Reynoldsovo číslo. Pomocí něho pak z aerodynamických charakteristik(polár) zvoleného profilu získáme součinitele odporu a hned potom poláru celého letounu, což jsme chtěli. Bez střední geometrické hloubky nosné plochy bychom však za Reynoldsovo číslo nepokročili a předběžný výpočet nedokončili.

Jestliže má plocha obdélníkový tvar pak dosazujeme za délkový rozměr do Reynoldsova čísla její hloubku. V tomto případě je střední geometrická hloubka právě rovná střední aerodynamické hloubce, takže je to jednoduché. V jiných případech tomu ale tak není.

Jestliže se mění tvar křídla, mění se i jeho hloubky podél rozpětí a to někdy dost značně. Tak se podél rozpětí mění i vztlak a odpor. Jakou tedy ale použít hodnotu pro výpočet? Nebo počítat každý kousek křídla zvlášť a pak je nějak sečíst? Ale jak?

Vychází se proto z předpokladu, že by dostatečně správnou polohou pro volbu vlastností celé nosné plochy mohlo být místo, kde se nachází těžiště jejího půdorysného tvaru. Není to vždycky pravda, protože jestli se Reynoldsovo číslo podél rozpětí mění komplikuje to značně získávání aerodynamických hodnot profilu(ů). Není proto ani prve uvedený předpoklad správný. Co je ale kolem nás úplně správné?

Nezbylo tedy nic jiného než se s tím smířit a velikost hloubky plochy v místě jejího těžiště používat s výše uvedeným předpokladem.

My se zde nebudeme zabývat výpočtem místa a velikosti střední aerodynamické tětivy. Uvedu pouze dva jednoduché postupy jak toho dosáhnout s přijatelnou přesností.

První z nich je geometrický způsob znázorněný v obrázku vpravo nahoře. Ten je však použitelný pouze u plochy s tvarem jednoduchého lichoběžníku. Jeho konstrukce je zřetelná a srozumitelná takže ji nebudu popisovat.

Druhý způsob má empirický nádech a je trochu méně přesný, ne však, pro předběžné úvahy, nepoužitelný. Zvolte tenký materiál stejnoměrného složení, narýsujte na něj v přijatelném měřítku půdorysný tvar jedné poloviny plochy a vystřihněte(vyřízněte). Pak tento výtvor podepírejte hranou pravítka tak dlouho, až zůstane ve vodorovné poloze. Tam je místo střední aerodynamické tětivy. Homogénost použitého materiálu je však podmínkou nutnou. Postup je znázorněn dole v obrázku.

Takhle se to tedy stručně má se střední aerodynamickou tětivou.