Co je co, co je to a kdo je kdo?
1. pokračování

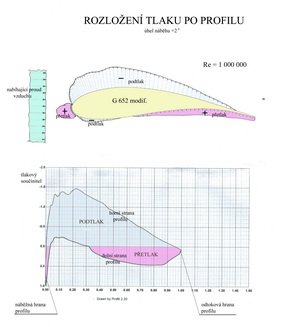
Vraťme se do 15., 16., 17 a 18.století kdy přes značný odpor církve začalo poznávání zákonů přírody soustavným a cílevědomým pozorováními a analyzou jejich výsledků, nikoliv jen přebíráním dřívějších, mnohem starších, informací z nichž některé byly staré dva i více tisíc let.

Před Galileem Galilei to byli : Mikuláš Kopernik, Tycho de Brahe, Johannes Kepler. Souběžně s ním ještě pak Evangelista Torricelli, Blaise Pascal ( dodnes je po něm nazvána jednotka tlaku), Robert Boyle a největší z nich Isaac Newton (po něm je pojmenována jednotka síly), který položil základy pohybu hmotných těles, mechaniky tekutin a formuloval gravitační zákon.

Ten popsal, mimo jiné, možné souvislosti týkající se proudění tekutiny kolem rovné desky položené pod určitým úhlem vůči směru proudění. Zde však neodhadl dost dobře vliv úhlu náběhu, což způsobilo v 19. století stavitelům létajících strojů mnoho potíží, protože hodnoty takto vypočtených výsledných aerodynamických sil byly velmi malé a nosné plochy proto zbytečně obrovské. Představil také svoji myšlenku o vazkosti tekutin a z nich vznikajícího tření nejen uvnitř tekutin, ale i o povrchy obtékaných těles. Citujeme: „Odpor způsobený nedostatečnou hladkostí vrstev tekutiny je za jinak stejných podmínek úměrný rychlosti, jíž se od sebe pohybující se vrstvy liší“.

Toho využili teprve po asi 150 letech Navier a Stokes k popisu dynamického stavu jednotlivých částic skutečné tekutiny. Ten byl ještě i po druhé světové válce dostupnými početními nástroji neřešitelný. Soustavu rovnic tohoto děje se podařilo vyřešit teprve před nedávnem pomocí obrovských moderních počítačů. Do té doby byla soustava rovnic řešitelná jen za určitých zjednodušení, například pro některé případy laminárního proudění nestlačitelné vazké (skutečné) tekutiny. Proto se ještě nedávno zjišťovaly aerodynamické charakteristiky(vztlak, odpor, moment, vznikající víry apod.) a z nich plynoucí výkony a vlastnosti létajících strojů výhradně v aerodynamických tunelech.

Souběžně s I. Newtonem a pak ještě po něm(zemřel roku 1728) propracovávali mechaniku tekutin Johanes (otec) a Daniel (syn) Bernoulliové. Významně jim pomohl dílo dokončit jeden z nejlepších matematiků světa Leonhard Euler. Tak vznikla známá Bernoulliho rovnice. Tu je možné velmi stručně vyjádřit asi takto : součet statického a kinetického tlaku je v ustáleně (na čase nezávisle) proudící nestlačitelné a neviskozní (bez vnitřního tření) tekutině stále stejný.

Abych nebyl tak necitelný a nezasypal čtenáře jenom takovýmito suchými informacemi připojuji dva obrázky, které využily Bernoulliho rovnice ke svému vzniku:

1. ke znázornění rozložení tlaků na profilu G 652 při úhlu náběhu 2^o a pro Re číslo 1 000 000, obr.č.1. Spodní diagram ukazuje na rozložení tlakového součinitele profilu pro jeho horní a dolní stranu. Povšimněte si jak je rozdělen přetlak(dolní strana a část přední) a podtlak(skoro celá horní strana) vůči proudu probíhajícího kolem. Z jejich součtu pak vznikne vztlak.

2. ke zvýraznění proměn rychlostí proudění podél profilu na obr.č.2 pro tentýž profil a za týchž podmínek proudění. Na horní straně profilu jsou místa, kde rychlosti proudění jsou až o více než 50% vyšší než rychlost V nabíhajícího proudu(nebo rychlost letu). Na spodní straně zase místa s rychlostmi až o cca 30% nižšími.

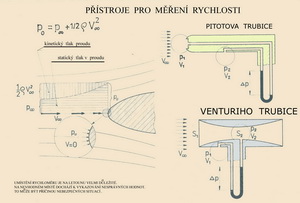
Oba tyto zjednodušené demonstrativní příklady platí pouze pro ideální tekutiny, tj. ty, které jsou bez tření. Mnohé souvislosti lze ale využít i pro skutečné tekutiny se třením.

Pro proudění skutečných(vazkých) tekutin pak platí :

Rovnice kontinuity, která vyjadřuje, že se v proudu tekutiny žádná hmota neztrácí a ani nevzniká. Je to tedy známý princip o zachování hmoty.

Pohybová rovnice určující dynamický stav jednotlivých částic proudící tekutiny, což je prve zmíněná soustava upravených Navier-Stokesových rovnic, vzniklých z Eulerovy rovnice, v té době již známé více než asi 70 let.

A pak přišli další a další zdatní jedinci, kteří podali vysvětlení souvisejících jevů a z toho plynoucích potřeb a možností k dalšímu využití v poznání světa kolem nás.

Vzpomeňme alespoň Henri Pitota (zemřel 1771), který poskytl jednoduchý prostředek, dodnes v různých obměnách využívaný, k měření rychlosti proudu z rozdílu statického a dynamického tlaku odvozených z Bernoulliho vztahu. Je to známá Pitotova trubice. Ta je společně s Venturiho trubicí na dalším obrázku.

Použité prameny:

• Bauer, Brůha, Jaňour -„Základy proudění“; 1950
• Nožička, Nožička –Průkopníci klouzavého letu ; 2002
• History of Flight ; www.century-of-flight.net
• Vlastní archiv.