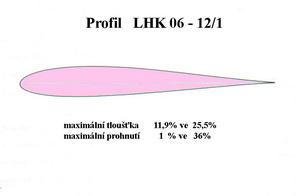
Profily nosných a ocasních ploch, listů vrtulí a rotorů
3.část

Posledně jsme skončili některými těžkostmi s nimiž se musí vypořádat proudící vzduch kolem těles v něm umístěných. My při tom na něm požadujeme, aby dal vzniknout co největšímu vztlaku, co nejmenšímu odporu, při ještě přijatelném nebo žádném klopném momentu.

Jak obtížné podmínky pro splnění těchto našich přání vytvářejí různě tvarovaná tělesa jsme již připomenuli dříve. Je to však ve skutečnosti ještě horší. Podívejme se nyní na rychlosti a tlaky vyskytující se kolem křídla létajícího stroje.

Dejme tomu, že se pohybujeme rychlostí 50m/s což je 180km/h. To není zase až tak závratná rychlost. Naše křídlo má střední hloubku 1m. Každá částice obtékajícího vzduchu má tedy pouze 1/50 sekundy na to, aby podél jeho hloubky společně s ostatními daly možnost vzniknout vztlaku a odpor potlačily co nejvíce. To se dále komplikuje, jak hned uvidíme, ještě tím, že rychlost se podél hloubky křídla mění. Z nulové rychlosti v okolí náběžné hrany vzrůstá v závislosti na tvaru profilu a úhlu náběhu velmi rychle na horní straně na dvojnásobek rychlosti letu. Na spodní straně jsou poměry obdobné nebo výrazně odlišné, což souvisí s tvarem profilu a jeho prohnutím.

Takže na horní straně zejména při větších úhlech náběhu mohou místní rychlosti dosahovat, v našem zvoleném příkladu, hodnot až 100 m/s. Pak se zase zmenšují, až v blízkosti odtokové hrany mají hodnoty blízké rychlosti letu. A to stále mluvíme o přilehlém proudění, které nevytváří velký úplav za profilem. Částice vzduchu se tedy na horní straně profilu urychlují až na dvojnásobek rychlosti letu, aby se zase prudce zpomalily k původním hodnotám. A to všechno za 0,02s.

Podobně se chová i tlak v bezprostřední blízkosti povrchu křídla. Viz Bernoulliho rovnice.

Jaké změny asi probíhají v poli vzduchu proudícího kolem křídla si dovede představit asi málokterý čtenář těchto stránek. Pokusíme se dodat několik doplňujících informací k osvětlení těchto jevů. Použijeme k tomu následující obrázky o průběhu rychlostí a tlaků vyskytujících se na profilu LHK 06 – 12/1.

Jeho aerodynamické charakteristiky jsou v dalším obrázku. Vidíte zde pět polár pro kritické (Re=70 000), mírně nadkritické (Re=100 000) až dostatečně vyvinuté proudění(Re= 500 000 a 1 000 000). Podrobněji je zatím nebudeme komentovat.

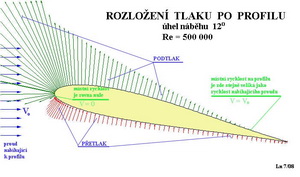
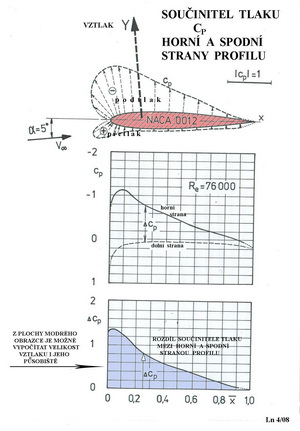
A konečně na následujícím obrázku je grafické znázornění průběhu tlaků podél hloubky tohoto profilu při úhlu náběhu(geometrickém) 12^o a Re=500 000.

Za povšimnutí jistě stojí ta obrovská podtlaková špička v horní přední části profilu, která signalizuje blížící se odtržení proudu od povrchu křídla. Prohlédněte i text na obrázku.

Na dalším obrázku je to trochu složitější, ale za to instruktivnější. V diagramu je na levé straně vynášen tlakový součinitel c_p , na vodorovné ose hloubka profilu a na pravé straně je svisle uváděn poměr V²/V_o². V_o je rychlost nabíhajícího proudu vzduchu(rychlost letu). V zastupuje místní rychlosti na profilu(nahoře nebo dole).

Tlakový součinitel je bezrozměrné číslo udávající změny tlaku a rychlosti na profilu. Jeho vztah vyhovuje přesně sice jen tekutinám bez vnitřního tření, ale pro naše poměry jsou průběhy tlaků a rychlostí dostatečně průkazné. Je odvozen z Bernoulliho rovnice za přispění jednoduchých matematických úprav pomocí dynamického a statického tlaku v proudící tekutině. Abychom to trochu zpestřili uvedeme ten výraz:

tlakový součinitel cp

C_p= ( p - p_o ) / ( 1/2 σ V_o² ) = 1 - ( V² / V_o²)

P – místní tlak na profilu ( + nebo -) [Pascal]

P_o; V_o- tlak a rychlost v okolním proudu [Pascal ; m/s]

σ – měrná hmotnost prostředí [kg/m³]

V – místní rychlost na profilu [m/s]

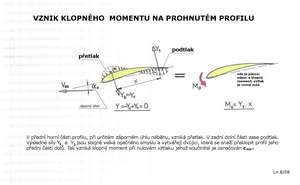
Malý průvodce diagramem:

-při tomto úhlu náběhu ( 12 stupňů ) vzniká obrovský podtlak hned za náběžnou hranou na horní straně a největší přetlak v asi 4% hloubky na dolní straně-zde je také místní rychlost proudu rovna nule

-podtlak na horní straně strmě klesá směrem k odtokové hraně, když asi v 90% hloubky je roven okolnímu tlaku v proudu

-odtoková hrana je v mírném přetlaku

-ze součtu obou místních tlaků a jejich průběhů, na dolní a horní straně, lze spočítat součinitel vztlaku a také působiště vztlaku.

Některé zajímavé body související s rychlostmi jsou v diagramu popsány, stejně jako údaje o tlacích na náběžné a odtokové hraně

Jestliže by se změnilo Re číslo nebo úhel náběhu nebo obojí, změní se výrazně i průběh místních tlaků a rychlostí.

Při nějakém záporném úhlu náběhu, to platí pro kladně prohnuté profily, budou plochy podtlaku a přetlaku na horní a dolní straně profilu v příslušném diagramu stejné. Protože však působí opačně bude výsledný vztlak roven nule. Těžiště těchto ploch nejsou však na jedné svislici a tak dvě stejně velké síly podtlaku a přetlaku(jejichž součtem je nulový vztlak) dávají tzv. dvojici sil, která se snaží profilem natočit směrem proti chodu hodinových ručiček(nosem profilu dolů). Vzniká tak klopný moment jehož součinitel c_mo při nulovém vztlaku je velmi důležitou aerodynamickou charakteristikou a provází profil neustále. Mění se s úhlem náběhu i Re číslem.

U dvojitě prohnutých profilů ( tzv. autostabilních) vzniká moment opačného smyslu, který se snaží zvedat nos profilu nahoru. Tyto profily musí mít proto těžiště před čtvrtinovým bodem.

Profily souměrné nemají žádný nebo jen nepatrný klopný moment.

To již jsme ale určitě dříve naznačili. Teď jsme si to dovolili pouze připomenout v souvislostech s tlakovým součinitelem.

Na dalším obrázku je výsledek mého měření profilu NACA 0012 v amatérsky postaveném tunelu před asi 30 lety.

Jedná se modelářské poměry odpovídající rozměrům nosné plochy malého modelu nebo ocasních ploch modelu většího. Úhel náběhu je 5 stupňů a Re=76 000. Vidíte, že průběh křivek součinitele tlaku je diametrálně odlišný od předchozího obrázku. Vypočítané působiště vztlaku je zde uvedeno.

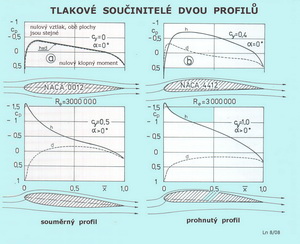
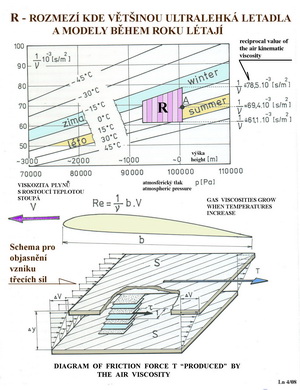
Z předchozího obrázku je zase patrné porovnání průběhu tlakových součinitelů dvou rozdílných profilů. Zvolená Re čísla odpovídají hodnotám menších skutečných letadel.

Nyní maličko odbočíme od tlaků a rychlostí a na dalším obrázku připomeneme prostory atmosféry Země kde ultralehká letadla a modely po většinu roku létají. Je to ten lichoběžník označený „R“.

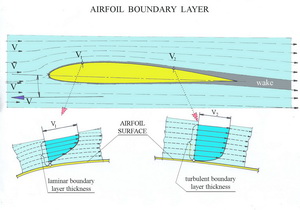
Ve střední části je znovu připomenuto Re číslo a skutečnosti, že vazkosti plynů se stoupající teplotou rostou a opačně. Je to obráceně než u kapalin. Vliv na průběh proudění je enormní.

V dolní části obrázku je pokus jak zobrazit vliv vnitřního tření v tekutinách. K dispozici jsou dvě desky se stejnou plochou S. Jedna z nich(spodní) je nepohyblivá a druhá ve vzdálenosti δy od ní se dala vlivem působení síly T do pohybu. Vlivem vnitřního tření v tekutině začne vrchní deska s sebou unášet nejbližší vrstvy tekutiny tak, že ta k ní nejbližší má stejnou rychlost jako deska. Ostatní vrstvy tekutiny se směrem dolů, k nepohyblivé desce, pohybují stále pomaleji, až ta poslední na ní ulpívá. Ve sledované vrstvě tekutiny je pak možné pozorovat rychlostní profil jednotlivých vrstev, který má přibližně přímkový průběh.

Je to jakési přiblížení jevů probíhajících v bezprostředních vzdálenostech od povrchů obtékaných těles. Tedy i povrchů létajících strojů.

Vrchní pohyblivou desku teď nahraďte vrstvou okolní proudící tekutiny o nějaké rychlosti V. V této vrstvě, kterou nazýváme mezní vrstvou, se mění rychlost proudu od nuly na povrchu letadla až na hodnoty místních rychlostí, které odpovídají předchozím obrázkům s tlakovým součinitelem. Na následujícím obrázku jsou to rychlosti V₁ a V₂.

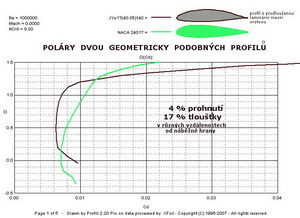
Charakter takové mezní vrstvy je odvislý od více okolností. Povšimněme si jednoho z nich. Tím je druh proudění k němuž v mezní vrstvě dochází. Jak jsme již uvedli dříve, viz i náš „Slovník vybraných pojmů“, existují v podstatě dva druhy proudění.

Je to proudění laminární, které je schematicky zachyceno vlevo dole na obrázku, s tvarem rychlostního proudu v jeho mezní vrstvě. Z něj je patrné, že rychlost od povrchu směrem do proudu narůstá pomalu, zejména zpočátku. To činí laminární mezní vrstvu značně nestálou, přestože její tloušťka je malá a proto i zde vznikající odpor není velký.

Malý odpor laminárního proudu, pokud k tomu má vytvořeny podmínky, je lákavou vidinou k použití na nosných a ocasních plochách létajících strojů. Ty podmínky musí být nejen vytvořeny vhodným návrhem, stavbou a použitou technologií, ale i během provozu udržovány, aby mohlo být laminární proudění zachováno. Což není jednoduché, protože například již jen znečištění předních částí nosných ploch nalepeným hmyzem nebo zvlnění jejich potahů při zatížení v letu, vytváří pro udržení laminárního proudění velké překážky.

K laminárnímu proudění může dojít téměř vždy na předních částech obtékaných těles(křídel) pokud k tomu jsou vytvořeny správné podmínky. K přechodu laminárního proudění v turbulentní má docházet co nejdále od náběžné hrany.

Proudění turbulentní zobrazené vpravo dole v tomtéž obrázku je od předchozího odlišné. Změny rychlostí proudu v mezní vrstvě jsou zde mnohem razantnější .Stabilita turbulentního proudu je sice proto mnohem větší než u proudění laminárního, ale za cenu větší tloušťky jeho mezní vrstvy a tím i většího, v ní vznikajícího, odporu.

O tom mohou podat svědectví následující tři obrázky. Jsou zde porovnávány vlastnosti dvou geometricky podobných profilů. Oba mají prohnutí 4% a tloušťku 17%, ale v různých vzdálenostech od náběžných hran. Tím je vytvořen předpoklad pro různé délky laminárního a turbulentního proudění.

Prvním z nich je profil ing J.Janovce - “JYs 17“ a druhým je programem Profili Pro vytvořený - „NACA 24017“.

Na prvním z obrázků jsou poláry obou profilů pro Re=1 000 000. Všimněte si rozdílných průběhů křivek v oblasti kdy je součinitel odporu( zde označený americkou zvyklostí c_d ) menší než 0,01. „JYs 17“ má podstatně menší odpor v poměrně širokém rozmezí součinitelů vztlaku ( zde označeném zase „americky“ jako c_l ).

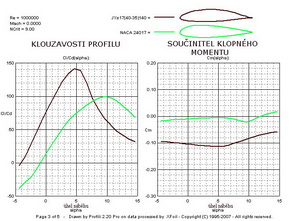
Další obrázek uvádí průběhy klouzavostí a součinitele klopného momentu v závislosti na úhlech náběhu. Janovcův profil má o 40% a více, větší klouzavost než NACA v rozmezí nejvyužívanějších letových poloh, tj. mezi úhly náběhu 0 až 7 stupňů.

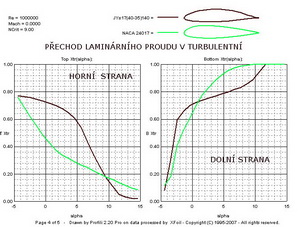
A nakonec je tu průběh poloh bodů přechodu laminárního proudu v turbulentní v závislosti na úhlu náběhu. Vidíte, že na horní straně profilu jsou v předpokládaných nejpoužívanějších letových režimech ( alpha -3 až + 8 stupňů) body přechodu jednoho proudění v druhé u Janovcova profilu mnohem dále od náběžné hrany než u NACA. To souvisí s oběma předchozími obrázky a v nich uvedenými aerodynamickými charakteristikami, jež jsou u Janovcova profilu s prodlouženým laminárním proudem podstatně lepší.

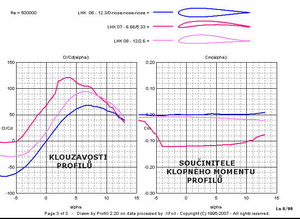
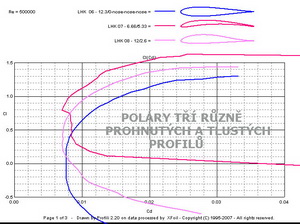
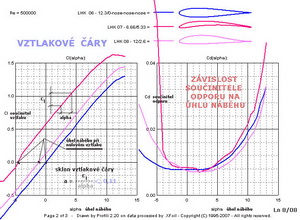
Teď se podívejme na průběhy součinitelů vztlaku, odporu a klopného momentu u třech zcela odlišných profilů. Jejich poláry pro Re=500 000 jsou na následujícím obrázku.

Horní profil z tohoto obrázku má souměrný tvar a tloušťku 12,3%. Jeho polární diagram je symetrický podél vodorovné osy, na níž je vynášen součinitel odporu.

Prostřední profil je z nich nejtenčí s tloušťkou kolem 6,7% ale s největším prohnutím asi 5,3%. Jeho polára je zcela nahoře.

Polára spodního profilu s prohnutím 2,6% a max. tloušťkou 12% se nachází mezi oběma předchozími.

Při tomto Re čísle jsou si velikosti minimálních součinitelů odporu dost blízké, jejich hodnoty jsou však přiřazeny různým velikostem součinitelů vztlaku.

Na dalším obrázku jsou dvě z aerodynamických charakteristik, a to součinitel vztlaku a součinitel odporu zachyceny v závislostech na úhlech náběhu. Re číslo je stále stejné jako prve. Všimněte si, že sklony vztlakových čar všech tří profilů jsou si velmi podobné.

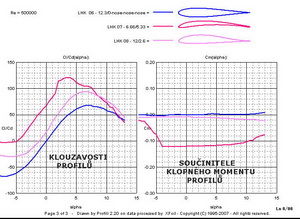
Jiné aerodynamické charakteristiky, klouzavosti profilů a součinitelé klopných momentů, uvedené v dalším obrázku si již tak podobné nejsou. Největších klouzavostí – největších aerodynamických jemností, dosahuje nejvíce prohnutý profil. Ten má však ale největší klopný moment, zhruba desetkrát větší než ostatní dva. To, a průběh spodní části jeho poláry, ho zčásti deklasují z létání vyššími rychlostmi na modelech.

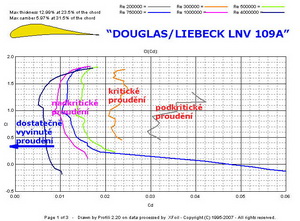
Prohnutý profil s tloušťkou 12% vykazuje ještě velmi dobré klouzavosti, má navíc velmi malý klopný moment a hodí se pro širší spektrum použití na létajících strojích.

Souměrný profil je na tom s aerodynamickou jemností nejhůře. Jeho prakticky nulový klopný moment a přijatelný odpor v širším rozsahu malých úhlů ( -5 ≤ α ≤ 5 ) náběhu ho směruje k použití na nosných plochách akrobatických strojů nebo SOP létajících strojů, obecně. Pro létání mezi pylony by však měl mít určité kladné prohnutí. Dejme tomu do 1,3%.

Aby si užili našeho mudrování i pravověrní zastánci zázračných profilů uvádíme malou galerii polár vybraných profilů.

Na tomto obrázku je Liebeckův profil LNV 109A , jehož zvláštní tvar i velké prohnutí jistě mnohé upoutá. Zkoušel jsem obdobný tvar na modelu kluzáku, s hloubkou nosné plochy kolem 200mm. Bez použití turbulátorů se pohyb modelu ve vzduchu nedal nazvat letem. Byl jsem někde vpravo v polárních souřadnicích zubaté křivky profilu s podkritickým prouděním. Aerodynamická jemnost profilu při Re=4 000 000 je však obrovská.

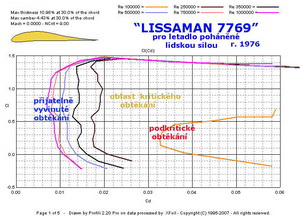
Další obrázek představuje jeden z profilů vyvinutý pro let lidskou silou a je od Lissamana z roku 1976. Je pro dané účely lepší než předchozí Liebeckův profil, přestože má nižší maximální součinitel vztlaku, protože má menší prohnutí.

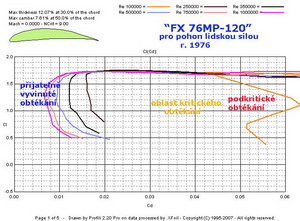
Pan prof. Wortmann tři roky před tím navrhl, pro stejné účely, svůj profil s tloušťkou 12% a obrovským prohnutím 7,6% a označil ho FX 76MP-120. Ten je na následujícím obrázku. Aerodynamickou jemnost profilu FX sice Lissamanův profil nepřekonal, ale byli to nakonec Američani, kdo dokázali uvést člověka(sice hubeného) na letadle vlastní silou do vzduchu a uletět s ním 1km.

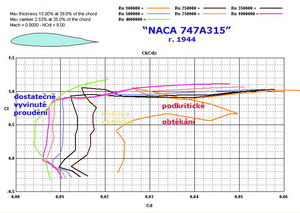
Vrátíme-li se do roku 1944 a vybereme z tehdejších rozsáhlých amerických podkladů například profil „NACA 747A315“, který je na následujícím obrázku, můžete snadno zjistit, že mohl být úspěšně používán u letadel u velmi rychlých letadel. Jeho odpor je velmi malý. Menší než například u Liebeckova „LNV 109A“. Ale aerodynamická jemnost výrazně horší. Stejně tak jako dosahované maximální součinitelé vztlaku.

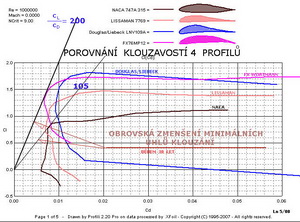
Pak je tu porovnání všech čtyřech předchozích profilů při Re=1 000 000 na dalším obrázku. Výsledkem dokonalejších prozkoumání vlastností mezních vrstev je téměř dvojnásobné zvětšení aerodynamické jemnosti od roku 1944 do nedávné doby. Výrazný pokrok přinesly například Wortmannovy práce v šedesátých letech 20. století.

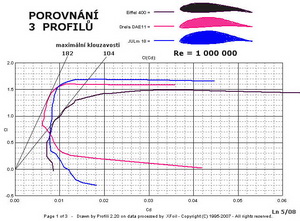
A konečně v posledním obrázku této části o profilech je porovnání tří profilů navržených v průběhu cca 90 let. „EIFFEL 400“ je z nich nejstarší. Americký „Drela DAE 11“ a český „JULm 18“ nejsou starší než asi 5 let. Rozdíl v dosažitelných klouzavostech je veliký.

Tím končí tato 4.část o profilech. V dalším pokračování se již dostaneme k polárám profilů a pokusíme se, aby se tvářily přátelštěji než se doposud mnohým příznivcům letectví zdá a více posloužily k pochopení toho co mohou nabídnout.