Slovník vybraných pojmů

A

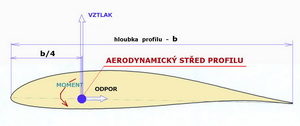
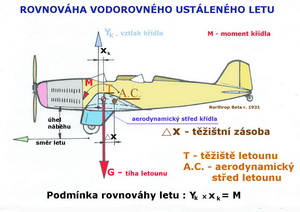
Aerodynamický střed (centrum) profilu, křídla nebo letounu je bod, ku kterému jsou momenty vznikající ze změn úhlů náběhu stálé.

Aerodynamický střed profilu se nachází přibližně v jedné čtvrtině jeho hloubky.
Aerodynamický střed křídla (nosné plochy) se nachází přibližně v jedné čtvrtině jeho střední aerodynamické tětivy.
Aerodynamický střed letounu s přirozeně fungující stabilitou by se měl nacházet vždy za jeho těžištěm.

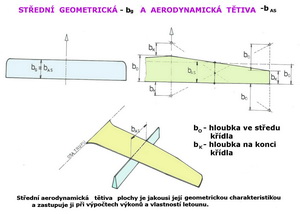
Pro dosažení stabilního letu je nutná vždy těžištní zásoba, která se pohybuje od cca 3% do 15% hloubky střední aerodynamické tětivy.

Aerodynamická tětiva je geometrická charakteristika nosné nebo ocasní plochy používaná při výpočtech výkonů a letových vlastností. Je nazývána střední aerodynamickou tětivou a obvykle je trochu větší než geometrická tětiva, která je hloubkou stejně velké obdélníkové plochy.

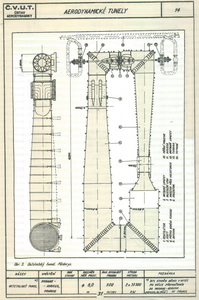
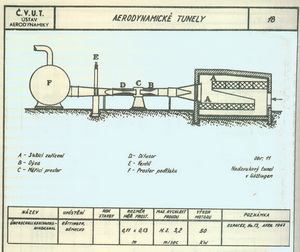
Aerodynamické tunely (AL 11/08 – Profily nosných a ocasních ploch – 5.část)

Všichni stavitelé létajících strojů a zejména jejich průkopníci v 19. století tušili a dodnes to vědí, že jejich znalosti o vztlaku a odporu nebyly a nejsou postačující. Proto začali stavět zařízení, která by jim umožnila dostat se v aerodynamice dále. Zpočátku to byly jakési „koloběhy“, kdy byly na přiměřeně velkém poloměru upevněny zkoušené předměty rotující kolem svislé osy. Toho využívali, mimo jiné, i Lilienthalové.

Pak se přišlo na to, možná, že to bylo i dříve, že by bylo možné využít nějakou“rouru“, profukovat jí vzduch a sledovat co to se zkoumaným tělesem, v ní umístěným, udělá. Tak začaly postupně vznikat větrné neboli aerodynamické tunely. Na obrázku je schéma tunelů, který používali Wrightové.

Postupem času vznikla taková monstra ke zkoumání aerodynamických vlastností profilů, křídel i celých letadel, že pro člověka neznalého dobře podstaty a cíle je jejich funkce stěží pochopitelná. Pak se přešlo od rychlostí proudů uvnitř tunelů, kolem asi 20m/s, k rychlostem přesahujícím rychlost zvuku několikanásobně a stále to pokračuje. První tunely byly v podstatě beztlakové. Průtočné nebo později cirkulační s uzavřenými nebo otevřenými měřícími prostory. Dále bylo nutno z důvodů zkoumání vlastností profilů při vyšších rychlostech než asi 150m/s přejít na tunely přetlakové.

Aerodynamickou laboratoř dnes naleznete na ploše několika tisíc metrů čtverečných a na první pohled ji nerozeznáte od nějakého průmyslového výrobního objektu. Je v ní zaměstnáno několik desítek až stovek vysoce kvalifikovaných lidí.

Následující obrázky jsou pouhým nástinem toho, co se v této branži dělo.

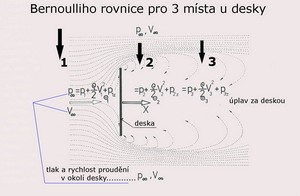
I když je dnes k dispozici mnoho výkonných počítačů a nemálo vhodných programů k získání aerodynamických charakteristik profilů, křídel i letadel jsou to stále ještě tunely, které poskytují základní i korekční informace pro navrhování létajících strojů.

B

Bernoulliho rovnice

( ρ/2 ) v² + p = konst.

Bernoulliho rovnice vzešlá z Eulerovy rovnice pro, v čase ustálený, pohyb dokonalé tekutiny rychlostí V říká, že součet dynamického tlaku(první člen levé strany rovnice) a tlaku statického(druhý člen levé strany rovnice) je stálý.

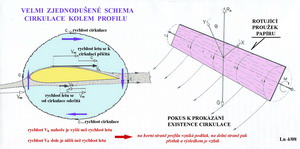
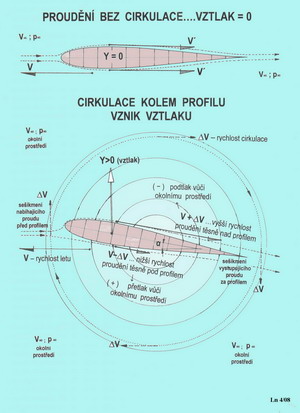
C

Cirkulace rychlosti při proudění

Tohle bude trochu náročnější na vnímání a dokonce i na přečtení. Pokusíme se představit okolnosti související s cirkulací rychlosti při proudění.

Jestliže předpokládáme, že tekutinu lze považovat za fyzikální kontinuum, tj.úplně a spojitě vyplňující daný prostor a že její nejmenší částečky mají stejné fyzikální vlastnosti jako její celek, pak jsme schopni například sledovat v určitém okamžiku stav celého proudu. Charakteristiky proudění jsou vázány na jednotlivé body uvažovaného prostoru, jemuž připisují kinematické vlastnosti.

Hmotný prvek, částice proudu, získává svoje dynamické vlastnosti teprve svým zařazením do tohoto kinematického prostoru, jež je zván rychlostním polem. V něm má každá částice proudu svoji rychlost danou její velikostí a směrem-vektorem.

Stav proudění vyjadřuje jeho proudnicový obraz. Takže ku příkladu při stálém(stacionárním) proudění jsou proudnice totožné s drahami částic proudu. S tímto stavem se nejčastěji v aerodynamice pracuje. My ho zde také využíváme.

Předním úkolem při proudění tekutin je stanovit rychlost jejich částic v libovolném bodě rychlostního pole proudu. Jsou tedy zkoumány poměrné přírůstky rychlostí částic ve třech souřadných osách. Částice se však nepohybují aniž by se při tom neotáčely. Tak vzniká vířivé pole proudění.

Jestliže bychom dokázali sečíst působení těchto vlivů na nějaké uzavřené křivce uvnitř tohoto pole, což se podařilo popsat již v 19. století např. Angličanu G.Stokesovi, tak tuto hodnotu nazýváme cirkulací rychlosti. Jedná se o výraz pro práci vykonanou vektorem rychlosti podél nějaké uzavřené křivky(a tou bude pro nás, po zjednodušení úvah, profil).

Tento jev je možné porovnat pro mnohé známým obrazcem rotačního proudění ve víru, který vznikne například ve vodě nebo při míchání kávy v šálku apod.

Jestliže vytvoříme představu, že do osy víru umístíme těleso jehož vnější tvary jsou ohraničeny uzavřenou křivkou(to je naše křídlo nekonečného rozpětí a tedy profil) vznikne kolem něho vírový pohyb a v něm se objeví cirkulace rychlosti víření. Smysl cirkulace u křídla je proti směru hodinových ručiček, nabíhá-li proud vzduchu z levé strany. Rychlost nabíhajícího proudu se nad křídlem zvětšuje o rychlost cirkulace a pod křídlem zase o ni zmenšuje. Tak dochází k rozdílným rychlostem proudění nad a pod křídlem, jejichž výsledkem je vztlak.

Před křídlem se směr nabíhajícího proudu vzduchu vlivem cirkulační rychlosti víru zvedá a za křídlem zase naopak klesá.

Aby to nebylo zase tak jednoduché, i když si mnozí čtenáři, pokud nějací byli, nejsou jisti ani tím co mohou z doposud zde sděleného využít, tak dopovím, že: cirkulace bez vztlaku, podle této teorie Žukovského a Kutty, není možná a opačně. Vztlak je tím větší, čím intenzivnější je cirkulace. A tak je to až dodnes.

Takhle nějak, jak ukazuje předchozí obrázek, to probíhá kolem profilu. V jeho pravé části je návod k uskutečnění jakéhosi ověřovacího experimentu pro přijmutí, prve, velmi kostrbatě, zjednodušeně a tím i ne úplně profesionálně vysvětlované existenci cirkulace kolem profilu.

Na dalším obrázku je učiněn pokus o zachycení cirkulace ve víru kolem křídla, který je částí vírového proudění kolem křídla konečného rozpětí.

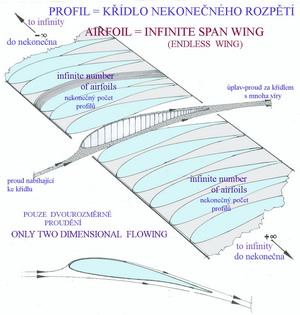
Okolnost, že na vír s cirkulací rychlosti, vázaný na křídlo v přímočarém proudění, působí vztlak má analogii v elektromagnetismu. Kolem přímočarého vodiče elektrického proudu se vytváří magnetické pole, jehož siločáry jsou kružnice kolem něj. Vytvářejí tak obrazec víru. Nachází-li se takový vodič v magnetickém poli, například mezi póly magnetu, působí na něj síla snažící se jím pohybovat napříč siločarami magnetického pole. Tato síla je analogická vztlaku.

(Tento odstavec je s malými změnami převzat z knihy Jaňour,Podzimek,Hacura – Základy aerodynamiky a mechaniky letu, r. 1953).

Pro sestavení celého tohoto povídání o cirkulaci bylo převážně použito knihy Bauer,Brůha,Jaňour- Základy proudění,Letecký průvodce 2, r.1950.

P

Profily nosných a ocasních ploch, ale i listů vrtulí a rotorů.

Co je to profil?

Profil je uzavřená rovinná křivka vzniklá řezem nosné či ocasní plochy a také listem vrtule nebo rotoru (a rovněž lopatkou rotačního stroje) v rovině kolmé na jejich podélnou osu.

Protože profil je pouze rovinným obrazcem nelze mu přiřazovat vlastnosti jimiž jsou vztlak, odpor, moment apod. Proto jej nahrazujeme při dalších úvahách pojmem křídla nekonečného rozpětí, u něhož již můžeme na důsledcích dvourozměrného obtékání kolem něj posuzovat jeho aerodynamické vlastnosti. Příklad křídla nekonečného rozpětí je na obrázku.

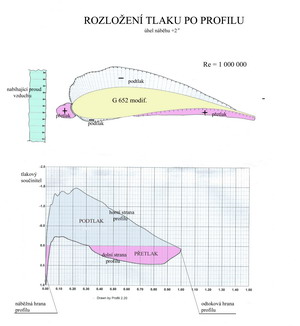
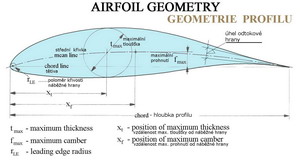
Abychom mohli porovnávat vlastnosti jednotlivých profilů je třeba je nějak geometricky popsat. Samotný tvar křivky nám nestačí. Proto je obrys profilu popsán vhodně zvoleným počtem souřadnic v pravoúhlém systému, které definují jeho tvar. V některých případech má souřadný systém počátek vlevo(na náběžné hraně) v jiných zase vpravo(na odtokové hraně). Na dalším obrázku je schéma profilu v souřadném systému s uvedením některých dalších geometrických charakteristik.

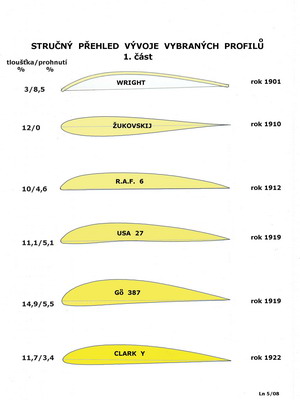
V předchozím obrázku jsou uvedeny zbývající základní geometrické charakteristiky profilu, které je vhodné pochopit a porozumět jim.

Jednotlivá letadla určená k různým účelům využívají přirozeně i profilů s různými tvary a vlastnostmi. Jeden profil není schopen vyhovět úspěšně zcela rozdílným požadavkům létajících strojů.

Na dalších dvou obrázcích je velmi stručně a nekompletně uveden pokus zachytit jakýsi vývoj profilů od počátku 20. století dodnes, pro oblast nižších rychlostí letu, dejme tomu do 450km/h.

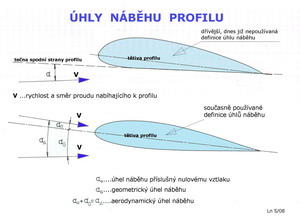
Aerodynamické vlastnosti profilů závisí nejen na jejich tvaru, ale také, mimo jiné, na poloze vůči směru letu. Tato skutečnost je vyjadřována úhlem, který svírá tětiva profilu se směrem letu(nebo jinak řečeno se směrem proudu nabíhajícího k němu). V aerodynamické praxi se obvykle lze setkat se třemi pojmy úhlů náběhu:

1.úhel náběhu při nulovém vztlaku profilu, který je pro prohnuté profily vždy záporný, ale pro souměrné profily je vždy roven nule

2. úhel náběhu sevřený mezi tětivou profilu a směrem letu, je to tzv. geometrický úhel náběhu. Ten může mít hodnoty kladné i záporné

3.konečně je to aerodynamický úhel náběhu, který je součtem obou dvou předchozích hodnot.

Všechny tyto úhly jsou na následujícím obrázku uvedeny. Je zde ještě připomínka dřívějšího způsobu vyjadřování úhlu náběhu profilu, který byl ale opuštěn kvůli nemožnosti jednotného posuzování různě tvarovaných profilů.

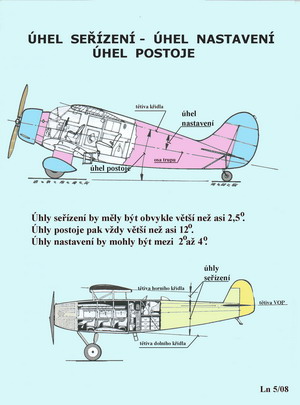
Pak jsou to ještě jiné úhly související s polohou profilu nosné plochy vůči létajícímu stroji na němž je použit. Viz další obrázek.

Jsou to následující pojmy, které by měly být používány s plnou zodpovědností k důležitostem, jaké zaujímají při návrhu letadla.

a)úhel nastavení je ten úhel, který svírá tětiva křídla s osou trupu

b)úhel seřízení je ten, který svírají tětivy křídla(křídel) s tětivou VOP

c)úhel postoje na Zemi je tím úhlem, který umožňuje využít co nejvyšší součinitele vztlaku při startu a přistání, aby k tomu potřebná dráha nebyla tak dlouhá a rychlosti, zejména při přistání, nepřiváděly posádku v úžas nad tím co mají ovládat.

Proudění laminární a turbulentní

Jestliže se pohybují částice proudu tak, aby se jejich dráhy nekřížily, tak pro takovýto druh proudění používáme názvu laminární. Je to proudění v tenkých vrstvách vzájemně se nemísících, takže se používá pro ně také pojmu – vrstevnaté proudění. Tento druh proudění se vyznačuje nízkým odporem, pokud jsou pro jeho vznik dodrženy nezbytné podmínky. Je ale také dost nestálé a když mu do cesty vstoupí nějaké překážky-zvětšená drsnost povrchu, prudká změna tvaru apod., ztratí svůj původní charakter a tím i svoji výhodu nízkého odporu.

Když se však částice proudu pohybují neuspořádaně, jejich dráhy se navzájem kříží, je takové proudění nazýváno prouděním turbulentním. Odpor těles tímto proudem obtékaných je oproti laminárnímu větší. Tento druh proudění má ale stálejší charakter a je schopen proudit kolem drsnějších povrchů, i těch co mění svůj tvar významněji, úspěšněji než proud laminární. Je to dáno hlavně příznivě působícími dynamickými účinky částeček proudu, které jsou odvozeny od jejich rychlostí.

V mnoha případech může být výsledný odpor turbulentního proudu nižší než u vynucovaného proudu laminárního.

Jestliže nastane laminární obtékání nějakého tělesa, čemuž dochází v jeho přední části prakticky vždy, pokud není výrazně zdrsněna či nevhodně tvarově deformována, přechází laminární proudění na nějaké části povrchu tělesa v proudění turbulentní. Pokud k tomu dochází, je možné postupně pečlivě tvarovat toto těleso a současně zjemňovat jeho povrch, s cílem prodloužit laminární proud co nejdále. Mnohdy tomu však tak není. Laminární proud se nestačí změnit v přilehlý proud turbulentní a od povrchu tělesa(nosné nebo ocasní plochy) se odtrhne. Vznikne tak obrovský nárůst odporu, který předchozí úsilí, o vytvoření co nejmenšího odporu vlivem využití laminárního proudu, zcela zhatí.

Na připojeném obrázku je schéma laminárního a turbulentního proudění, na příkladu rovné desky postavené rovnoběžně se směrem proudu, ukázáno.

S

Stoupání létajícího stroje

Stoupavý let je jedním z manévrů létajících strojů, je-li k dispozici přebytek výkonu pohonné jednotky.

Pro dosažení ustáleného stoupavého letu je třeba zachovat rovnováhu působících sil. V podstatě se při stoupání jedná o zvedání letounu do výšky požadovanou rychlostí stoupání a zároveň o překonávání odporu při tomto letu vznikajícím. Obvykle se stoupání posuzuje při nějakém úhlu stoupání, kterému při dané výkonnosti odpovídá určitá rychlost letu.

Na připojeném obrázku jsou vzorec pro výpočet rychlosti stoupání pro zvolený úhel a k tomu nezbytný komentář, zachyceny.

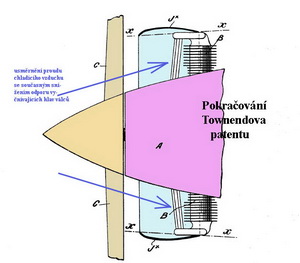
T

Townendův prstenec ( AL 1/09 – Ohlédnutí do minulosti – 5.část)

Hvězdicové motory vrtulových pohonných jednotek, dříve hojně používané, byly zdrojem zvýšeného odporu létajících strojů. Jednak měly válce, obvykle jich bylo kolem devíti a více, umístěné na poměrně velkém průměru a jednak je bylo třeba dobře chladit, takže je nebylo možno příliš ukrývat v obrysech trupů.

Výsledkem mnohého „přemýšlování“ ve třicátých letech 20. století pak byl návrh upravit kryt motoru tak, aby byl snížen odpor a zajištěno dostatečné chlazení.

A tak spatřil světlo světa návrh Angličana, jménem Hubert Charles Henry Townend, který byl patentován například v Kanadě 14.10.1930. Jedno ze schémat patentové přihlášky je na připojeném obrázku. Je doprovázen obrázkem s jednou z aplikací na francouzském turistickém hornoplošníku „Phrygane“ z roku 1935.

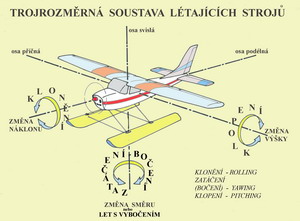
O nějakou dobu později byl v USA v National Advisory Comitee for Aeronautics navržen obdobný kryt s prodlouženou hloubkou stěny – „N.A.C.A. cowling“, který se pak také hojně používal.

Trojrozměrná soustava létajících strojů

Trojrozměrná soustava sestávající ze tří os s počátkem umístěným v těžišti letounu(modelu), umožňuje určení na něj působících sil a momentů.

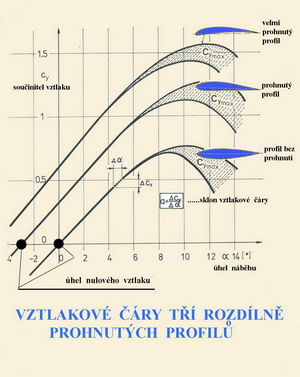
Vyjádření sil a momentů v aerodynamické souřadnicové soustavě, včetně používaného názvosloví je uvedeno v následující tabulce:

Osa podélná

odpor X(Q), součinitel odporu cx ,

X=c_x . ρ/2 . V² . S

charakteristický rozměr – velikost nosné plochy…..S

klonivý moment , součinitel klonivého momentu mx , M_x=m_x . ρ/2 . V² . S . l

charakteristický rozměr – rozpětí nosné plochy …. l

Osa svislá

vztlak Y , součinitel vztlaku cy , Y= c_y . ρ/2 . V² . S

zatáčivý moment , součinitel zatáčivého momentu my , M_y= m_y . ρ/2 . V² . S . l

charakteristický rozměr - rozpětí nosné plochy…..l

Osa příčná

příčná síla Z , součinitel příčné síly cz , Z=c_z . ρ/2 . V² . S

klopivý moment , součinitel klopivého momentu mz , M_z=m_z . ρ/2 . V² . S . bAS

charakteristický rozměr-střední aerodynam. tětiva…..b_AS.

Všimněte si, že ve všech vzorcích je zastoupen dynamický tlak ρ/2.V² proudu vzduchu nabíhajícího na nosnou plochu, jinak řečeno je to při rychlosti letu V.

V

Vztlakové čáry profilů

„Posláním“ každého profilu nosné nebo ocasní plochy je vytvářet vztlak. Odpor při tom vznikající je obvykle nutným průvodním zlem.

Jednou z aerodynamických charakteristik profilu je průběh součinitele vztlaku na úhlech náběhu. Vztlak je hlavně ovlivněn prohnutím profilu a rozložením tloušťky po jeho hloubce.

Při dostatečně rozvinutém proudění kolem profilu má vztlaková čára, ve své převážné části, tvar přímky. Ve své horní části je vždy zakřivena u vyšších úhlů náběhu směrem doprava(k větším součinitelům odporu), dosahuje svého maxima a po jeho překročení klesá dolů. Odpor při tom stále narůstá. Jestliže je průběh její horní části plochý, tj. s malým zakřivením, jedná se obvykle o nezáludný profil u něhož dochází k odtrhávání proudu postupně od odtokové hrany kupředu. Jestliže má však její horní část zakřivení velké, s prudkým poklesem hodnot součinitele vztlaku, nelze očekávat pohodu při létání s velkými úhly náběhu.

Na připojeném obrázku jsou tři příklady vztlakových čar různě prohnutých profilů zachyceny.

W

Winglety

Nejprve připomeneme anglický výraz, kterým je „washout“. To je případ kdy se snažíme upravit tvary a tím i vlastnosti křídla jestliže opatrně a rozvážně působíme na rozložení vztlaku podél jeho rozpětí. Vztlak je obvykle největší uprostřed křídla a směrem ke koncům klesá až na nulu. Zde, bez dalšího vysvětlování, upozorníme na metodu Multhopovu, Schrenkovu či Prandtlovu, které nezbytně provázejí designéry nosných ploch již po mnoho desetiletí. Jedná se mimo jiné o to, aby nedocházelo k prvotnímu odtrhávání proudu vzduchu od křídla v oblasti křidélek. To je velmi nežádoucí. Zmíněné metody spojené s úpravami tvarů křídel tomu pomáhají zabránit. Celkový dosažitelný vztlak křídla však poněkud klesne.

Winglety, což jsou nástavby pevných křídel letadel, mají právě opačnou úlohu než „washout“, podporují efektivnější využití vztlaku vyvozovaného na koncích křídla. Používá se pro to i výraz „aerodynamic wash-in“. Winglety by tedy měly působit podobně příznivě jako zvýšení štíhlosti křídla, aniž by se muselo zvětšovat jeho rozpětí. Tím zlepšují využití vztlaku na okrajích křídel a také zmenšují indukovaný odpor způsobený okrajovými víry křídla.

To znamená, že se příznivě uplatní při letech s většími úhly náběhu. Při létání s menšími součiniteli vztlaku, tj. při přeskocích kluzáků z jednoho místa na druhé, ač se u některých větroňů používají, mohou být při nesprávném návrhu spíše brzdou. Zejména v případech nevhodně volených a vůči okrajovým vírům nesprávně nastavených profilů.

Winglety však také tím, že „zachraňují“ část vztlaku u konců křídel, vytvářejí větší kroutící moment na křídle a to vede přes jeho nutné zpevnění v kroucení k jeho vyšším hmotnostem. Mohou také vyvolat zvýšený požadavek na washout kvůli citlivosti na spirální nestabilitu a tím i ke zhoršení optimálního rozložení vztlaku u daného tvaru křídla.

Jako jeden z prvních použil winglety Rutan na své „Vari Eze“ v roce 1975.

Na následujícím obrázku je ukázka wingletu na křídle velkého dopravního letadla.

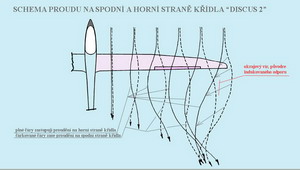
Další obrázek přibližuje schema proudění na spodní a horní straně jedné poloviny křídla . Zaznamenejte jak je obrazec proudění na horní straně „vyboulen“ směrem ke středu křídla a proudění na spodní straně zase k jeho okrajům. Tomu mají částečně zabránit winglety a pomoci tak snížit celkový odpor křídla při částečném zisku vztlaku.

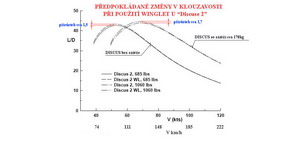
A na dalším obrázku je diagram předpokládaných průběhů klouzavostí u větroně Discus 2 , jednou se zatížením nosné plochy a podruhé bez něj, jestliže jsou či nejsou použity winglety. Jaké, to se neuvádí. Z diagramu je patrno, že přírůstky klouzavostí nejsou závratné i když jsou nějaké očekávány.

Od čeho je odvozeno slovo winglet přesně nevíme.

Mohlo by to však být spojeno s tím, že Angličan Fr.W.Lanchester v roce 1897 patentoval, kvůli ovlivnění vírů vznikajících na koncích křídel konečných rozpětí, „wing-end-plates“. Z toho mohl název winglet vzniknout. Je to však pouze naše domněnka.