Polára profilu
neboli
křídla nekonečného rozpětí

Tak jsme se konečně dočkali dlouho očekávané, aspoň v to doufám, instrukce o tom co může dokázat profil nosné nebo ocasní plochy, listu vrtule nebo rotoru, či lopatky dmychadla nebo jiného obdobného rotačního stroje.

Když jsme již přežili povídání o rychlostech a tlacích při proudění a z toho vznikajících sil a momentů působících na létající stroj za jeho pohybu v atmosféře Země, když jsme přežili Bernoulliovu rovnici, Reynoldsovo číslo atd., tak se podívejme na to co může nastat jestliže máme k dispozici uzavřenou křivku vhodného tvaru, zvanou profil, což je, lépe řečeno, vlastně křídlo nekonečného rozpětí. Protože jakýpak vztlak, odpor či moment může vykázat rovinná křivka-profil.

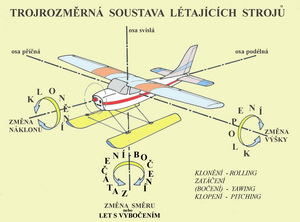
Sestavíme-li ale z nekonečného počtu takových křivek obdélníkové křídlo máme k dispozici nástroj, sice virtuální, protože ho neumíme sestrojit, ale pro posouzení vlastností profilu z nichž je sestaven, nástroj velmi dobrý. Nás totiž nyní bude zajímat pouze rovinné proudění, tj. pohyby částic vzduchu dozadu, dopředu , nahoru a dolů ve smyslu souřadných os x a y (viz trojrozměrná aerodynamická soustava). Nikoliv do stran, vlevo nebo vpravo ve smyslu osy z. To si ponecháme do další kapitoly, kdy se poučíme o křídlu konečného rozpětí, které již zhotovit umíme.

Obrázek křídla nekonečného rozpětí jsme již publikovali dříve. Stejně jako geometrické charakteristiky a názvosloví, jež se toho(profilu) týkají. Také jsme již uvedli vztahy pro výpočet aerodynamických sil a momentu. Viz např. následující pasáž z e Sborníků vybraných pojmů o Trojrozměrné soustavě létajících strojů.

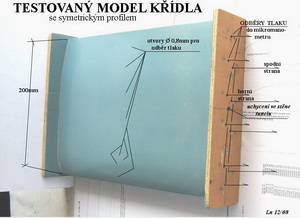
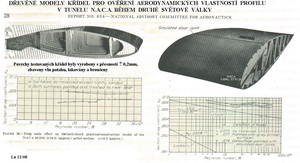
Stručný souhrn informací, pro zopakování, byl uveden v minulém čísle Akademie letectví v kapitole O profilech…

Pokud se chceme dobrat pochopení informací z toho co poskytují poláry profilů je třeba trochu osvětlit význam součinitelů vztlaku, odporu, momentu a výsledné aerodynamické síly.

Již od dob Newtonových, následně od Bernoulliho a pak mnoha dalších se ví jak vyjádřit dynamický účinek proudu tekutiny. Nejprve určíme velikost tlaku odvislého od pohybu tekutiny. Ten se zapíše takto

p = ρ/2. V² .... (kg/m.s² = Pa)

zde je : ρ- hustota tekutiny (kg/m³), V – rychlost proudění (m/s) .

Působí-li takovýto tlak na nějakou plochu, například plochu křídla, vyvolá sílu odpovídající její velikosti a předešle uvedenému dynamickému tlaku. Takže například odpor, jakožto výslednou sílu působícího dynamického tlaku proudu na danou ploch S (m²) bychom mohli získat takto:

X = p . S ... (kg.m/s²)

Ve skutečnosti je to trochu komplikovanější, protože záleží na poloze této plochy vůči směru proudění a také na jejím tvaru. A to platí nejen pro plochy, ale i pro tělesa.

Takže je nutné, na základě experimentálních výsledků, prve uvedený vztah trochu upravit. A sice tak, že do něj vložíme tzv. součinitel. To je bezrozměrné číslo, které v sobě zahrnuje vliv polohy a tvaru plochy. Zároveň, jak již jsme poznamenali několikrát dříve, i vliv velikosti Reynoldsova čísla.

Výsledný vztah pro aerodynamickou sílu, v tomto případě odpor, bude pak mít následující tvar

X = c_x . p . S ... (kg . m/ s²)

Podobně můžeme zapsat výrazy pro vztlak, moment a výslednou aerodynamickou sílu(což je geometrický součet vztlaku a odporu).

Odborný pojem součinitelů je v aerodynamice důležitý proto, že pomocí nich můžeme obecně popisovat jevy a předpovídat jejich průběh, aniž bychom museli znát velikosti těles(ploch) a dynamické tlaky konkrétního proudu. Potřebujeme však znát Reynoldsovo číslo.

Jak toho lze dosáhnout? Například měřením v aerodynamických tunelech a správným vyhodnocením získaných údajů.

To pochopil již i O.Lilienthal v 90.letech 19. století a z výsledků svých pokusů sestavil diagram s počátkem souřadnic – pólem ( proto polární diagram a zkráceně polára) odkud byly vynášeny vektory součinitele výsledné aerodynamické síly c_R v závislosti na příslušném úhlu náběhu, který svírala zakřivená deska se směrem proudění.

Vztah mezi součinitelem výsledné aerodynamické síly a mezi součinitelem odporu c_x a součinitelem vztlaku c_y je následující:

c²_R = c²_x + c²_y

Takovouto, Lilenthalovu poláru jsme již prezentovali dříve. Na vodorovnou osu jsou při tom vynášeny součinitele odporu a na osu svislou součinitele vztlaku ( dřívější americké podklady to znázorňují opačně).

Jestliže sestavíme takovýto diagram, z údajů získaných dříve pouze měřením v tunelech a dnes již také pomocí výpočtových programů, pak můžeme společně se vztlakovou a momentovou čarou, které se obvykle uvádějí zvlášť, získat potřebné aerodynamické charakteristiky profilu. U každé takové charakteristiky je třeba uvést hodnotu Reynoldsova čísla, abychom věděli jaké poměry panovaly při jejím získání(vypočtení).

Polára profilu je tedy grafické znázornění závislostí mezi součinitelem vztlaku a součinitelem odporu při daném Reynoldsově čísle. Tato závislost může být také vyjádřena pouze číselně ve formě vhodné tabulky, která však není na první pohled dostatečně vypovídající o vlastnostech profilu. Je však vhodnější pro další výpočty( podívejte se na předchozí číslo Akademie v článku profilech).

Jak součinitelé vztlaku, odporu a momentu získáme skutečně?!

1. V tunelu:

1a) proměřováním místních tlaků na horním a spodním povrchu testovaného obdélníkového křídla podél jeho hloubky z nichž potom sestavíme průběh tlakových součinitelů(viz minulé číslo Akademie nebo Soubor vybraných pojmů) a z nich vztlak a jeho působiště a potom výpočtem součinitele vztlaku

1b) proměřováním tlaků v úplavu za testovaným křídlem a z toho pak odpor a jeho součinitele.

Na připojeném obrázku je příklad takového modelu křídla, který jsem před lety použil při měřeních v mém vlastním tunelu, kde jsou patrny otvory na horním povrchu křídla a výstupní otvory po pravé straně k mikromanometru k zaznamenání místních tlaků. Model je uložen ve stěnách tunelu.

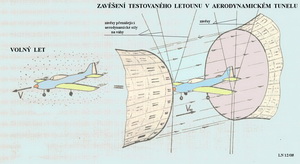
1c) vyhodnocením sil celkového vztlaku, odporu a momentu na modelu křídla zavěšeného pomocí tenkých lanek na vahách umístěných mimo tunel. Ze zjištěných hodnot se pak stanoví příslušné součinitelé. U této metody je třeba obezřetné použití korekčních hodnot pro závěsy modelu křídla a také kvůli konečnosti jeho rozpětí. Model je upevněn uprostřed měřícího prostoru tunelu. To jsme uskutečnili s Ing.Hořením na počátku 70.let 20. století a publikovali jsme výsledky, které nezůstaly bez povšimnutí například u p. Jedelského nebo u p. prof. Epplera. Oba je komentovali s překvapením, protože při tak nízkých Re číslech nebyly do té doby takové informace zveřejněny. Později naše měření otiskli, a nejenom oni, ve svých publikacích.

V laboratořích například americké N.A.C.A a samozřejmě také německé v Gőttingen bylo proměřeno mnoho profilů. Na dalším obrázku je model křídla N.A.C.A jaký byl používán při testování profilů během druhé světové války.

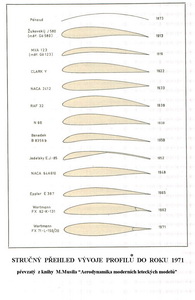
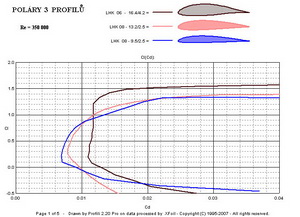
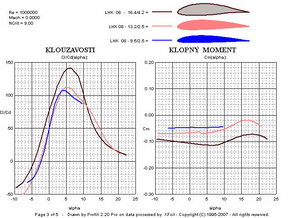
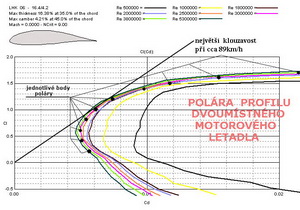
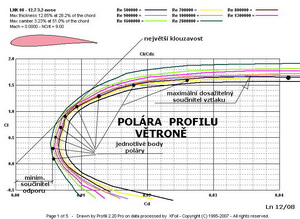
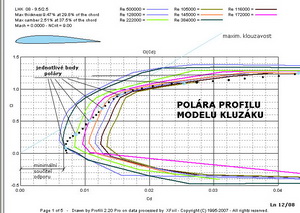
Předmětem našeho zájmu v tomto článku tedy budou součinitele – vztlaku, odporu a momentu. Dále by nás měly zajímat odpovídající úhly náběhu měřených profilů a také hodnoty Reynoldsových čísel, při nichž byly prve uvedené údaje získány.

Toho lze dosáhnout například měřením v tunelu nebo pomocí vhodného výpočetního programu, který je ale také založen na mnoha předcházejících měřeních.

Abych například prokázal vliv maximální tloušťky na aerodynamické vlastnosti a výkony profilu vybral jsem tři profily o tloušťkách – 16,4; 13,2 a 9,5%. Navíc jsem použil výsledky při podmínkách kdy je proudění již přijatelně vyvinuté (Re=350 000) a pak v podmínkách ještě lepších (Re=1 000 000).

Polární diagramy(poláry) všech tří profilů jsou pro obě Re čísla na dalších dvou obrázcích.

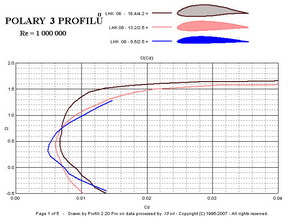
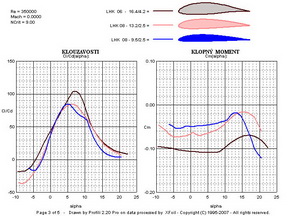
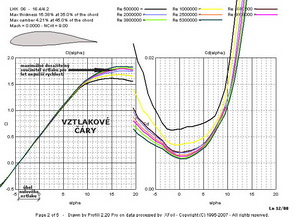
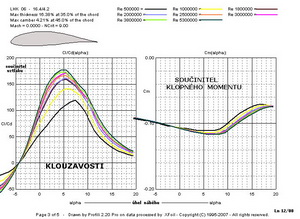
Z nich je patrné, že tenký profil s tloušťkou 9,5%(označený 1)má v levém diagramu nejmenší odpor, ze všech tří, kolem hodnoty součinitele odporu 0,005 při součiniteli vztlaku cca 0,1. Podmínky proudění mu tedy již dost dobře vyhovují. Jeho maximální součinitel je však, ale nejmenší ze všech.

Středně tlustý profil s tloušťkou 13,2%(označený 2) je za stejných podmínek již také dost dobře obtékán, ale jeho výsledky jsou poněkud horší ve srovnání s tenkým. Jeho nejmenší součinitel odporu má hodnotu cca 0,0058 při součiniteli vztlaku 0,3.

Nejtlustší, 16,4%-ní, profil(označený 3) dosahuje nejmenšího součinitele odporu cca 0,011 při součiniteli vztlaku cca 0,2. Nad tímto bodem však následuje velmi příznivý průběh poláry až do součinitele vztlaku cca 1,2(součinitel odporu se jen velmi málo zvětšuje). Dosahovaný maximální součinitel vztlaku cca 1,57 je největší hodnotou ze všech tří.

Pravý horní diagram při větším Re čísle napovídá, že profily 1 a 2 sice zlepšily svoje parametry, ale méně než profil 3. Jeho nejmenší součinitel odporu se zmenšil výrazně na hodnotu cca 0,0067.

Následující obrázky to mohou potvrdit. Jedná se o klouzavosti a součinitele klopného momentu.

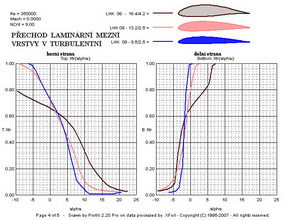
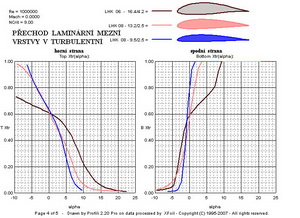
V klouzavostech je výrazně nejlepší nejtlustší profil 3. Hodnoty klopných momentů se nijak zvlášť výrazně nezměnily.

Další dva obrázky ukazují na průběh přechodů laminárních mezních vrstev v turbulentní. Nejtlustší profil je na tom hůře při záporných úhlech náběhu na horní straně avšak při úhlech nad cca 2 stupně začíná být výrazně lepší. Na spodní straně je tomu obdobně.

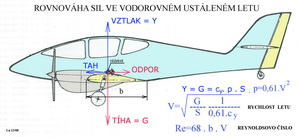
Tak a co teď?!?!

Teď už jenom to, že se konečně dostáváme k určení poláry profilu. K tomu však přece jen ještě něco málo potřebujeme udělat.

1. Je třeba zvolit létající stroj a jeho důležité geometrické parametry- například nosnou plochu, tíhu, rozpětí atd.

2. Z nich určit zatížení nosné plochy a pak rychlosti letu pro zvolený rozsah součinitelů vztlaku.

3. Pak již jen spočítat Re číslo náležející zvoleným součinitelům vztlaku.

4. U zvolených součinitelů vztlaku najít příslušnou poláru odpovídající příslušnému Re číslu a označit tuto polohu v diagramu.

5. Spojením takto získaných bodů nakreslit poláru křídla nekonečného rozpětí(profilu).

A také potřebujeme připomenout jak to asi vypadá se silami ve vodorovném ustáleném letu, z něhož budeme vycházet. Je to vyznačeno v následujícím obrázku.

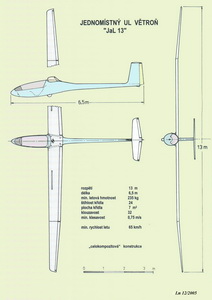
A JE TO !!!

Ale co? Co to je?......Je to polára křídla nekonečného rozpětí(profilu) pro dané zatížení jeho nosné plochy. Ještě to ale není ani polára skutečného křídla a již vůbec ne polára letadla(vydržte ještě do příštího čísla AL).

Jak uvidíte prochází šikmo napříč polárami pro jednotlivá Re čísla a má docela jiný tvar než jakákoliv předchozí z nich, protože již respektuje rozdílné rychlosti letu.

Zvolili jsme prve tři profily různých tloušťek a teď na příkladech zase tří k nim přiřazených příkladů létajících strojů zkonstruujeme poláry jejich profilů(křídel nekonečných rozpětí), abychom poznali rozdíly s nimiž se můžeme setkat při takové práci.

Tak první létající stroj, z dalšího obrázku, je fiktivní dvoumístný dolnoplošník s předpokládanou letovou hmotností 500kg a nosnou plochou 12,6m² , takže její zatížení je cca 400N/m². Střední aerodynamická tětiva je cca 1,35m.

A nyní je třeba počítat, jiná možnost již nezbývá.

a)Pro vybrané součinitele vztlaku vypočítáme rychlosti a z nich potom Reynoldsova čísla. K tomu použijete výrazů z předchozího obrázku. Pro výpočet rychlosti by bylo správnější použít součinitele výsledné aerodynamické síly namísto součinitele vztlaku. Ale rozdíl je malý.

součinitele vztlaku cy	0,2	0,4	0,6	0,8	1	1,2	1,4	1,5	1,7
rychlosti letu V m/s	57,2	40,5	33	28,6	25,6	23,4	21,6	20,9	19,6
Re číslo 10-6	5,25	3,72	3,03	2,63	2,35	2,15	1,98	1,92	1,8

b)Pomocí nich, na původních hodnotách součinitelů vztlaku, zjistíme interpolací, mezi nejbližšími hodnotami Re čísel, jednotlivé body poláry profilu daného stroje

c)spojením těchto bodů získáme celou poláru profilu se střední aerodynamickou tětivou 1,35m nosné plochy při zatížení 400N/m² létajícího stroje.

Další dva obrázky obsahují vztlakové čáry profilu, klouzavosti a součinitele klopného momentu v rozsahu zkoumaných Re čísel.

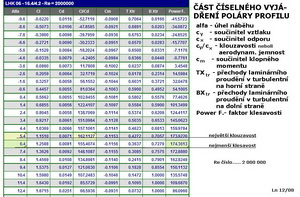
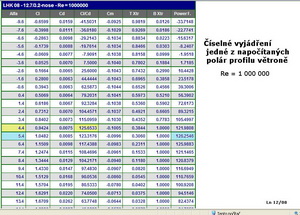
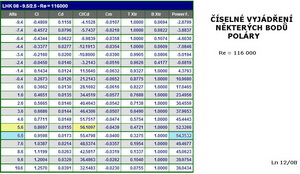
A to je již všechno o profilu, který můžeme, když budeme chtít, použít pro dvoumístný motorový létající stroj.

Na dalším obrázku je číselné vyjádření výpočtu poláry pro jedno Reynoldsovo číslo jak to vyhodnotil program „PROFILI.2.20.Pro“. V něm naleznete přesnější údaje pro případnou korekci výpočtu.

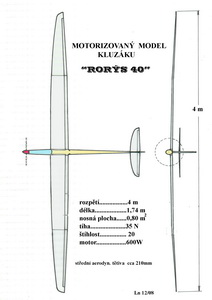
A stejným způsobem je možné sestavit poláru křídla nekonečného rozpětí pro větroně z obr.č. 71 a pro model z obr.č. 72. Ty jsou společně s číselnými vyjádřeními v dalších čtyřech obrázcích.

To jsou, znovu si dovoluji upozornit na to, pouze poláry profilů –křídel nekonečných rozpětí, se zvoleným plošným zatížením uvedených tří létajících strojů.

Příště to bude již polára křídla konečného rozpětí, které umíme sestrojit a hlavně vyrobit. Uvidíte jaký zásah do předchozích polár to udělá.