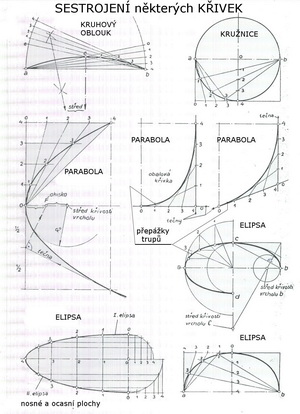
Některé veličiny z matematiky a fyziky, s nimiž se setkáváme v letectví a bez nichž se stěží obejdeme

Stává se nezřídka, že je vhodné připomenout některé okolnosti bez nichž se stěží obejdeme, chceme-li se zahloubat alespoň trochu více do letectví s jeho létajícími stroji a porozumět důležitým zákonitostem s tím spojených.

Domnívám se, že by to mohly být tentokrát konstrukce některých vybraných křivek, často se vyskytujících při stavbě létajících strojů a také některé fyzikální a matematické veličiny, o jejichž existenci sice vědí všichni absolventi středních škol, ale na něž si již snadno nevzpomínají. Pokusím se je poněkud přiblížit v jejich chápání a snad i užívání.

Následující obrázek předvádí jak je možné kdekoliv zkonstruovat tři kuželosečky-kružnici, elipsu a parabolu, jejichž tvary můžeme dobře využít při navrhování létajících strojů, ať malých či velkých. Je zde jeden způsob konstrukce kruhového oblouku s nalezením středu křivosti, dále kružnice o zvoleném poloměru(když pro ně nemáme vhodné kružítko), čtyři konstrukce elipsy a tři konstrukce paraboly.

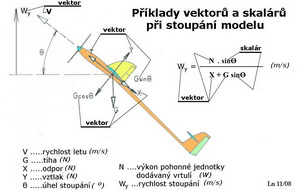
A pak je tu zopakování zjednodušených definic vybraných matematických a fyzikálních veličin metrické soustavy, které jsou nejen v letectví používány.

Skalár je fyzikální veličina, u níž známe pouze velikost(např. je to hmotnost, práce, teplo,..) Skaláry můžeme sčítat, odečítat, dělit i násobit.

Vektor je fyzikální veličina u níž známe nejen velikost, ale i směr, též zvaný smysl, kterým může působit(síla, rychlost, zrychlení, tlak,..). Práce s vektory spočívá v jejich sčítání i odčítání a to algebraicky a geometricky.

Dráha je vzdálenost mezi (obvykle) dvěma zvolenými místy(body). Jednotkou dráhy(vzdálenosti) je 1m - jeden metr (je to skalár).

Čas je úsek doby, který uběhne mezi dvěma pozorovanými jevy(je to skalár). Jednotkou času je 1s - sekunda (minuta, hodina, rok,…). O čase toho mnoho nevíme. Není známo kdy začal a kdy skončí. Můžeme ho jen sledovat jak plyne.

Rychlost udává délku dráhy proběhnutou za jednotku času. Jednotkou rychlosti je 1 m/s - metr za sekundu (je to vektor). Dalšími používanými jednotkami mohou být km/h, míle/h, uzly apod.

Zrychlení pohybu, stejně jako jeho zpomalení(zbrzdění), udává jak se mění velikost rychlosti s časem. Jednotkou zrychlení(zpomalení) pohybu je 1m/s²-metr za sekundu na druhou (je to vektor, protože má velikost i směr).

Hmotnost tělesa, jakéhokoliv tvaru nebo velikosti, udává jaké množství nějaké látky(vzduch, voda, kovy, …) je v něm obsaženo. Jednotkou hmotnosti je 1 kg (je to skalár).

Síla je výsledným účinkem vzájemných působení mezi hmotnými tělesy. Při sledování jejich účinků musíme udat i její působiště, tj.odkud a kam působí. Jednotkou síly je 1N – newton (je to vektor). Jeho rozměr je kg.m/s². Sílu 1N je třeba vyvinout, abychom tělesu o hmotnosti 1kg udělili zrychlení 1m/s².

Tíha tělesa je síla jaká na něj v klidu působí směrem do středu Země, např. na podložku na níž je postaveno(je to vektor).

Práce vzniká působením síly po nějaké dráze. Je to také množství energie vložené do této činnosti.

Jednotkou práce je 1J - joule(je to skalár).

1J= 1N.m= kg.m²/s².

Výkon představuje množství práce vložené do nějaké činnosti za jednotku času. Jednotkou výkonu je 1W-watt(je to skalár).

1W= 1J/s= 1kg.m²/s³.

Tlak vzniká působením silového pole na nějakou plochu. Jednotkou tlaku je 1Pa-pascal(je to vektor).

1Pa= 1N/m²=1kg/m.s².

Účinnost nějakého děje(procesu) udává poměr hodnoty jakou je možné na jeho konci využít z hodnoty do něj zpočátku vložené. Je to vždy číslo menší než 1 nebo menší než 100 (pracujeme-li s %). Účinnost se obvykle označuje řeckým písmenem η. Nemá žádný fyzikální rozměr a je to skalár.

Mohli bychom uvést ještě další jednotky používané v technických návrzích strojů a zařízení různého účelu, například Ampér, Volt,.., ale nám by prve uvedené zatím mohly stačit.

Na dalších dvou obrázcích jsou uvedeny příklady vektorů v označování některých dějů v mechanice letu. Snad jsou dostatečně srozumitelné pro všechny čtenáře magazínu i pro ty, kteří nejsou úplně zběhlí v analyzování ustálených průběhů a dějů a z toho plynoucích závěrů pro následná konstruování.

Jedná se letové manévry - stoupání nebo klesání létajících strojů, které jsou v nich popsány vektory a skaláry a jejich výslednými výpočetními vztahy, jež byly z těchto obrazců odvozeny.

Osmělím se uvést dva příklady využití prve uvedeného textu:

a)jestliže mluvíme o váze letadla a vyjadřujeme ji v kg, pak je jediný správný výraz pro to – hmotnost

b)když však chceme vyjádřit silové působení letadla jakožto hmotného tělesa je nutné použít výrazu - tíha, protože se jedná o sílu a udat ji v N ( kg.m/s²), nikoliv v kg.

Ještě dodám, že je dost často používán převod kilogramů na newtony. Zde platí následující vztah 1kg= 9,81N. Ten je nutno používat například tak, že těleso o hmotnosti jednoho kilogramu je přitahováno k Zemi silou 9,81 newtonů.

A nakonec jedno doporučení pro případné nadšence snažící se sestavit jiné než dosud známé výpočtové vztahy, aby nezapomněli vždy zkontrolovat platnost výsledného vztahu pomocí dimenzionální homogenity. Tím je míněno to, že v konečném výpočtu nemůže mít například rychlost rozměr třeba kg.m/s, nebo W, ale jen a jen m/s. Jinak je někde v analýze děje nebo v následné početní rutině chyba.

Vřele doporučuji takováto dobrodružství podstoupit, protože v jeho průběhu vždy objevíte dosud pro vás skryté souvislosti a nakonec dojdete ke správnému pochopení děje. Vyhledáte pak počítač s vhodným programem a vytvoříte svůj vlastní, do něhož budete jen dosazovat jiné vstupní údaje a během zlomků sekund dostanete postupně mnoho variant řešení.