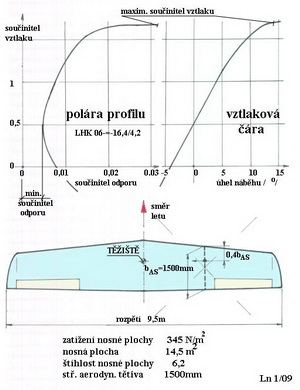
Polára křídla

Další aerodynamickou charakteristikou letadla s nepohyblivou nosnou plochou je polára jeho křídla. Teď již ne obdélníkového křídla nekonečného rozpětí (s tím jsme se vypořádali již minule), ale křídla skutečného, které chceme postavit. Stojí ještě za povšimnutí, jak se od sebe poláry profilů uvedených tří příkladů letadel v minulém čísle magazínu, liší.

Co máme a co k tomu ještě potřebujeme, abychom získali poláru křídla?

Máme poláry profilu pro potřebný rozsah Reynoldsových čísel, odpovídajících nekonečnému křídlu se zatížením, které se budeme snažit dodržet, k čemuž nás vede přepokládaná výsledná letová tíha stroje. Tím jsme již rozhodli například přibližně o tom jakou minimální rychlost letu bude takovýto stroj se zvoleným profilem schopen dodržet. Skutečná minimální rychlost letu bude o něco vyšší, jak poznáme záhy.

Polára a vztlaková čára profilu LHK 06-16,4/4,2 , s nímž uvažujeme od minula do křídla letadla, jsou v horní části následujícího obrázku.

Ve spodní části tohoto obrázku je půdorysný tvar křídla a jeho rozměry. Velikost nosné plochy je cca 14,5m² a její střední aerodynamická tětiva cca 1500mm. A jak teď dál?

Je třeba zavzpomínat na to co se děje kolem křídla konečných tvarů. Připomeneme pouze, že na jeho spodní straně, v obvyklé poloze letadla, je přetlak vůči okolnímu prostředí a na horní straně zase podtlak. Jejich působením na nosnou plochu vznikne vztlak. To již známe a také víme, že na obou okrajích křídla dochází k vyrovnávání tlaků pod a nad ním za vzniku nemalého víru, který přidává letadlu odpor. To se nám sice nelíbí, ale nezbývá než se s tím vyrovnat a dokonce smířit.

Jak velký vliv má toto vyrovnávání tlaků na obou okrajích křídla, za vzniku tzv. indukovaného odporu, na výkony letadla nám napoví štíhlost a tvar křídla. Aniž bych obtěžoval všelikými odvozeními poznamenám, že velikost indukovaného odporu lze snadno spočítat podle následujícího jednoduchého vztahu :

c_xi= ( c_y² / ( π . λ ) ) . konst

kde:

   c_y je součinitel vztlaku

   π je Ludolfovo číslo ..3,14159

   λ je štíhlost křídla

   konst zahrnuje vliv půdorysného tvaru křídla a má hodnotu od 1 do cca 1,2

Když se obrníme trpělivostí a spočítáme hodnoty indukovaného odporu pro zvolené součinitelé vztlaku za použití hodnoty štíhlosti z předchozího obrázku a konst= cca 1,08 získáme údaje o součinitelích odporu o něž musíme zvětšit hodnoty profilových odporů z poláry profilu. Spojnice těchto bodů vytvoří parabolickou křivku s vrcholem v počátku (pólu) poláry.

Takže je můžeme spočítat pro štíhlost 6,2 a odhadnutou konstantu pro lichoběžníkový půdorys křídla konst= 1,08 . Matematická formulka pro součinitel indukovaného odporu pak bude mít tvar:

c_xi = ( c_y² / ( π . 6,2 ) ) . 1,08 = 0,0555 c_y²

Součinitel vztlaku profilu

cy	0,2	0,4	0,6	0,8	1	1,2	1,4	1,5	1,7

Součinitel indukovaného odporu

cxi .103	2,2	8,8	20	35,5	55,5	80	108,8	124,9	160,4

Součinitelé odporu křídla(nosné plochy) c_xk budou součtem hodnot součinitelů odporu profilu(polára profilu v minulém čísle AL nebo ta v horní části předešlého obrázku) a součinitelů prve spočítaného součinitele indukovaného odporu :

c_xk = c_xp + c_xi

cxp.103	5,67	5,1	4,95	5,38	6,2	7,38	9,75	11,68	15,45

Součinitel odporu křídla:

cxk.103	7,87	13,9	24,95	40,88	61,7	87,38	117,75	136,58	175,85

Porovnáte-li ještě hodnoty součinitelů odporu profilu s hodnotami součinitelů indukovaného odporu zjistíte, že jsou srovnatelné pouze při malých součinitelích vztlaku. Pak začíná dost rychle významným způsobem převažovat vliv indukovaného odporu. Proč to asi je???

Je to proto, že námi navrhované křídlo má poměrně malou štíhlost. Kdybychom štíhlost zvětšili na příklad 1,5x, tak klesne indukovaný odpor také 1,5x, ale celkový odpor křídla se tak příznivě nezmenší, protože odpor samotného profilu bude přinejmenším stejný jako u štíhlosti předchozí, pokud nebude trochu větší vlivem nižšího Re čísla.

To byl jen takový demonstrativní příklad a upozornění na poměrný vliv součinitelů indukovaného ( a v něm hodnoty štíhlosti křídla) a profilového odporu.

Nyní jsme schopni spočítat aerodynamické jemnosti křídla(klouzavosti) z poměru součinitele vztlaku a jemu odpovídajícího součinitele odporu křídla .

Klouzavosti křídla :

cy/cxk	25,4	28,8	24	19,6	16,2	13,7	11,9	11	9,7

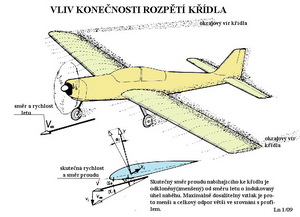
Jak to ale je ve skutečnosti??? ( je vhodné malé opakování).

Protože skutečné letouny nemají křídla nekonečných rozpětí vzniká kolem nich složitější proudění. Proudění není již, jako je tomu u pouhého profilu, pouze rovinné(dvojrozměrné), ale trojrozměrné. Čím blíže k okrajům křídla, tím více se uplatňuje i složka proudu působící podél rozpětí.

Na dalším obrázku je schematicky uvedeno oč se asi jedná.

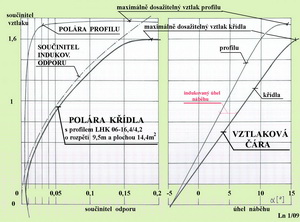
Křídlo nastavené pod určitým úhlem náběhu ke směru letu vyvozuje vztlak, jakožto součet přetlakových sil pod ním a podtlakových sil nad ním. Tato tlaková pole se vyrovnávají jak v úplavu za křídlem, tak i na obou jeho koncích(okrajích). Tak vzniká složka proudění podél rozpětí a sice dole od středu křídla k oběma koncům a na straně horní směrem ke středu.

Ve vírech kolem křídla je mařena určitá energie, kterou létající stroj nenávratně ztrácí a je u křídla konečného rozpětí větší právě o ztrátu energie v okrajových vírech. Důsledkem toho je vyšší odpor a nižší dosažitelný vztlak skutečného křídla oproti profilu(ů), který je v něm použit.

Vírový pohyb vzduchu kolem křídla(vzpomeňte na cirkulaci kolem profilu) odchyluje původní směr proudu nabíhajícího na křídlo o rychlosti V_∞ . Skutečně působící proud na křídlo o rychlosti V je odkloněn o tzv. indukovanou složku v_i dolů. Hodnoty rychlostí se od sebe příliš neliší, jejich směry však ano. A to tím více, čím většího vztlaku se snažíme dosáhnout.

Skutečné křídlo je pak obtékáno proudem vzduchu pod menším úhlem náběhu α_e ve srovnání s původně předpokládaným α (viz obrázek). Jejich rozdíl je zván indukovaným úhlem náběhu α_i. Tato změna směru skutečného proudění má za následek odchýlení vztlaku směrem po proudu právě o indukovaný úhel náběhu. Jeho část(průmět do směru letu) vytváří tak, zdánlivě paradoxně u vztlaku, přídavný, jinak již nám svým názvem známý, indukovaný odpor. To je jeden důsledek křídla konečných rozměrů.

Druhým důsledkem je nemožnost dosáhnout stejného maximálního součinitele vztlaku jako u profilu, protože stavu proudění kolem tohoto křídla, kdy může nastat odtržení proudu, je již dosaženo při skutečném úhlu náběhu menším než u profilu.

Doplňujeme jakousi útěchu – indukovaný odpor nevzniká u skutečného křídla, které nevyvozuje vztlak. Na to si vzpomeneme, ale jen ve střemhlavém letu, o který mnohdy ani nemusíme stát.

Aerodynamické charakteristiky křídla konečného rozpětí se tedy oproti charakteristikám samotného profilu, vždy zhorší.

Velikost indukovaného odporu je možné do jisté míry omezit vhodnými opatřeními, kterými mohou být například winglety nebo jiné účinné úpravy konců křídel, včetně jejich aerodynamického a geometrického kroucení.

Nepříznivé účinky indukovaných jevů se při letech velmi blízko povrchu Země zmenšují. To sice usnadňuje starty, ale zase prodlužuje přistání.

V následujícím obrázku je grafické znázornění předchozího početního postupu pro získání poláry skutečného křídla. Polára profilu je vytažena slabou čarou a průběh součinitelů indukovaného odporu čarou čerchovanou. Výsledná polára křídla je pak znázorněna silnou, plnou čarou.

Všimněte si jak polára křídla značně kopíruje parabolický tvar křivky součinitelů indukovaného odporu. Na tom je založena jedna z přibližných výpočtových metod výkonů letadel, kdy je s polárou matematicky „zacházeno“ jako s parabolou prognózovaného tvaru. To ale nyní není náš případ.

A jsou tu ještě, v pravé části tohoto obrázku, vztlakové čáry skutečného křídla a profilu. Podívejte se jak se vztlaková čára křídla nejen sklonila, ale ještě snížila svůj vrchol, takže maximálně dosažitelný součinitel vztlaku je tu jen asi 1,6.

Jak k tomu došlo?

Bylo třeba spočítat hodnoty indukovaných úhlů náběhu pro již dříve zvolené součinitele vztlaku podle tohoto vztahu

α_i = 57,3 . c_y / ( π . λ )      [ ^o ]

a pak je sečíst s původními hodnotami úhlů náběhu α, čímž jsme získali nové hodnoty úhlů náběhu α_e s nimiž nyní nabíhá proud vzduchu ke křídlu, aby se pokusilo dosáhnout dříve zvolených součinitelů vztlaku. Jak rychle uvidíte z následující tabulky, již se mu to nepodařilo.

αi	0,64	1,3	1,94	2,6	3,2	3,8	4,4	4,8	5,4	[ o ]
α	-2,6	-1	0,7	2,5	4,1	6	7,9	9	15	[ o ]
αe	-1,96	0,3	2,64	5,1	7,3	9,8	12,3	13,8	20,4	[ o ]

Proč?

Ze vztlakové čáry profilu je patrné, že maximum součinitele vztlaku je cca 1,75 při úhlu náběhu cca 15,5^o odpovídajícímu dvourozměrnému proudění. Při dalším zvětšování úhlu náběhu již vztlak nestoupá, ale jen klesá. Znamená to, že profil není schopen při větším úhlu náběhu zvyšovat vztlak. A také to znamená, že maximálního součinitele vztlaku bude tedy schopen dosahovat v nejlepším případě při α_e = 15,5^o. Tato hodnota se nachází v předchozí tabulce výpočtu úhlů náběhu při trojrozměrném proudění přibližně uprostřed mezi hodnotami součinitele vztlaku 1,5 ≤ α_e ≤ 1,75 . Takže interpolací v tomto rozmezí úhlů náběhu můžeme určit maximálně dosažitelný součinitel vztlaku u našeho skutečného křídla v hodnotě cca 1,6. A to je právě se změněným sklonem vztlakové čáry a tvarem horní části poláry z předchozího obrázku patrné.

Naše skutečné křídlo se štíhlostí 6,2 tedy nebude schopno vyvozovat větší součinitel vztlaku než asi 1,6 a jeho účinnost se, až na případ kdy c_y = 0, zhorší a to tím více, čím větších úhlů náběhu bude využívat. A jeho předpokládaná minimální rychlost letu se při stejném zatížení nosné plochy zvýší cca √1,75/1,6 = 1,05krát.

A to jsou, mimo jiné důsledky konečnosti rozpětí a půdorysného tvaru nosné plochy. Pak mohou přicházet v úvahu vlivy způsobené výrazným poklesem Re čísel u konců křídel, což jsou případy všech modelů letadel a mnoha větroňů s velkými štíhlostmi apod.

Tím asi dnes skončíme, aby toho nebylo zase příliš na urovnání a vyhodnocení předložených informací a s vědomím toho, že jsme jen velmi stručně a přibližně přiblížili možný postup při pátrání po tom, jaké výkony může poskytnout samotné křídlo daných rozměrů a tvarů létajícímu stroji u něhož známe jeho předpokládanou tíhu.

Příště se pokusíme posoudit celý létající stroj s tímto křídlem.