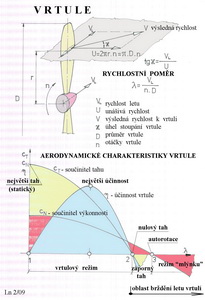
Otázky našich příznivců
a naše odpovědi

OTÁZKY

V.R. 3.2.2009

Vliv pevné nebo volně se otáčející vrtule na výkony elektroletu?!?!

1. Má volně se otáčející vrtule větší odpor než zabržděná?

2. Když ano tak:

  a) proč

  b) když má vrtule větší odpor tak proč se nezastaví?

3. Když ne, tak proč má model s volně se otáčející vrtulí horší klouzavost?

NAŠE ODPOVĚDI

Nejprve na otázku č.3.

Volně se otáčející vrtule nevyvozuje patrně žádný vztlak působící proti tíze modelu. Protože je klouzavost poměrem vztlaku ku odporu a tazatel nabyl zkušenosti(í), že model má s otáčející se vrtulí horší klouzavost, pak se musel zvětšit odpor modelu zřejmě přispěním otáčející se vrtule. Otáčející se vrtule měla tedy větší odpor než vrtule pevná. Důkazy se pokusíme podat v dalším textu.

Otáčela se ale vrtule zcela volně nebo přemáhala ještě nějaké jiné odpory než svoje vlastní?

Kdyby tomu tak bylo a vrtule se otáčela zcela volně, pak by byly znevěrohodněny nesčíslné dřívější zkušenosti s volně se otáčejícími vrtulemi u modelů poháněných gumovými svazky. Což se neprokázalo. Naopak výkony těchto modelů, ve srovnání s těmi co měly nepohyblivé vrtule v klouzavém letu, mírně stouply.

A teď na zbývající otázky.

K tomu ale potřebujeme něco málo informací o tom jak si vrtule počíná ve vzduchu. Některé argumenty je třeba také podepřít jednoduchými matematickými popisy. Bez toho se neobejdeme, jinak by to bylo málo smyslné tlachání, které přenecháme jiným, například do nějakého parlamentu.

Teď zaostřete na následující obrázek, kde jsou některé charakteristiky vrtule uvedeny.

Nejprve je nutné si ujasnit několik pojmů a výrazů. Ty jsou uvedeny v horní části obrázku.

Na každý element vrtule „dotírá“ jiná rychlost obtékajícího vzduchu, zde označená V. Tato rychlost je geometrickým součtem(vzpomeňte na sčítání vektorů, jež jsme již uvedli dříve) rychlosti letu V_L a rychlosti unášivé(rotace) U. Výsledná rychlost svírá s rovinou rotace úhel κ (kapa).

Jestliže uvedeme rotující vrtuli do pohybu můžeme s výhodou popisu jejich vlastností použít poměru rychlosti dopředného pohybu(letu) V_L a součinu otáček a průměru vrtule(ve jmenovateli). Tomuto výrazu se říká rychlostní poměr. Pomocí něho lze popsat pohyb vrtule ve vzduchu.

U vrtule nás zajímá především velikost tahu, který je schopna vyvinout a výkon, který je schopna přenést z motoru na letoun. Obě tyto veličiny vztaženy pomocí součinitele tahu c_T a součinitele výkonnosti c_N ku rychlostnímu poměru λ mají pak stejnou funkci jakou součinitele vztlaku a odporu v závislosti na úhlu náběhu(což již známe).

A teď ke spodní části obrázku. Zde jsou na svislou osu vynášeny součinitele tahu a výkonnosti společně s účinností vrtule. Na ose vodorovné je průběh rychlostního poměru.

V bodě 1 stojí otáčející se vrtule na místě a má největší tah, protože zkroucený list vrtule je ofukován po celé své délce(poloměru) pod velkými úhly náběhu. Pokud jsou takto posuzovány vrtule s většími hodnotami stoupání pak se setkáme s velkým spotřebovávaným výkonem motoru a také často s velkým hlukem způsobeným odtrháváním proudu od listů. Účinnost je rovna nule, přes značný příkon, protože vrtule stojí na místě a nekoná proto svým tahem užitečnou práci. V podstatě pouze rozhání vzduch.

Jestliže se letoun dá s rotující vrtulí do pohybu dostáváme se do tzv. vrtulového režimu, kdy účinnost celého procesu nejprve rychle stoupá, aby po dosažení svého maxima začala zase klesat. Když stále zvyšujeme rychlostní poměr λ, k tomu dochází např.při stejných anebo menších otáčkách a snahou o zvýšení rychlosti letu, využitelný tah vrtule se zcela vytratí stejně tak jako účinnost. Pro to, aby se vrtule mohla stále otáčet i v tomto režimu potřebuje nezbytnou výkonnost pro překonání aerodynamických odporů. Je to bod 2 v diagramu.

Naší snahou je proto vždy zvolit pro svůj létající stroj takový rychlostní poměr, aby účinnost vrtule byla co největší. S tím bezprostředně souvisí i volby průměru a úhlů nastavení listů. To je dost komplikovaná záležitost, kterou teď nebudeme vysvětlovat.

Při dalším zvětšování λ se dostáváme s vrtulí do režimu brzdění. Vrtule mezi body 2 a 3 vyvozuje záporný tah(proti směru letu a tedy se sčítá s celkovým odporem), i když stále ještě nějakou výkonnost spotřebovává.

Jakoukoliv výkonnost přestane vrtule potřebovat dostane-li se do režimu autorotace, je to bod 3, kdy se samovolně otáčí(pokud jí v tom nebrání nějaké odpory). Takhle běžně pracují rotory vírníků a také rotory vrtulníků při sestupu bez motoru.

Dalším posunutím na ose rychlostního poměru vpravo se dostane vrtule do tzv. režimu „mlýnku“, kdy sice stále brzdí, ale je již schopna dodávat výkonnost. To je princip využívaný u větrných elektráren nebo pro znovu spuštění motoru letadla dynamickým účinkem vzduchu při zvýšené rychlosti klouzavého letu.

To byl jen velmi stručný výklad o tom, jak se může vrtule chovat při různých velikostech rychlostního poměru λ, který je přímo úměrný rychlosti letu a nepřímo úměrný součinu otáček a jejího průměru.

A teď pokus o zodpovězení zbývajících otázek.

Podle nesčíslných zkušeností s „volnoběhem“ vrtulí u dřívějších modelů poháněných gumovým svazkem lze usuzovat na to, že jejich stojící vrtule o velkém průměru a stoupání a tím i značného čelního průřezu, měly větší odpor než později používané vrtule volnoběžné.

U dnešní elektroletů nebo i jiných modelů mohou mít používané vrtule jiných tvarů a čelních ploch odpory menší než tytéž vrtule nacházející se v brzdném režimu, za bodem 2 diagramu.

Přestože neznáme žádné bližší údaje o velikosti stroje, pohonné jednotce, vrtuli, rychlostech letu atd. od tazatele, pokusíme se spekulovat o tom co bylo pozorováno.

Předpokládejme, že máme elektrolet o nosné ploše cca 0,35m² ,pohybující se ve stoupání rychlostí cca 20m/s, při otáčkách vrtule 9000 ot./min, která má ø 300mm.

a) Těmto poměrům odpovídá rychlostní poměr v hodnotě cca 0,444 a ten určuje, že úhel jakým nabíhá proud vzduchu k vrtuli na 70% průměru má velikost 11,4^o. Přiřadíme-li k tomu ještě úhel náběhu 5^o je úhel nastavení listu k rovině rotace v tomto místě 16,4^o .

b) V bezmotorovém letu má volně otáčející se vrtule, dejme tomu, 10 ot/s a rychlost letu je 7m/s. Rychlostní poměr má nyní hodnotu cca 2,33(5 x větší než prve). Úhel proudu nabíhajícího k vrtuli má, i s původním úhlem náběhu, hodnotu cca 41,7^o. List vrtule je nyní v tomto místě obtékán proudem s úhlem náběhu 41,7 – 16,4= 25,3^o. A teď následuje odvážný odhad, ne však asi příliš přehnaný, o tom co se zde děje. Zřejmě zde vzniká výsledná aerodynamická se záporným součinitelem vztlaku. Zvolme jeho hodnotu c_y = -0,5. Vrtule za těchto podmínek vyvozuje tedy záporný tah o velikosti cca 0,17N.

c) Celkový odpor modelu bude při odhadnutém součiniteli odporu c_x= 0,055 asi X = 0,58N. Jestliže se k tomu nyní přidá prve spočítaný záporný tah volně se otáčející vrtule bude nyní klouzavý let brzděn silou 0,58 + 0,17 = 0,75N. A to je o cca 30% více než byl celkový odpor modelu. O tolik se tedy zhorší i klouzavost, čehož si musel každý všimnout a proto asi také vznikl tento dotaz. Odpor stojící vrtule může být v našem případě asi 0,16N.

Víc si zatím netroufáme předložit v odpovědi na dotaz, protože ve skutečnosti je to nepochybně poněkud složitější. Snad to postačí pro upozornění na to, že volně se otáčející vrtule spalovacích a elektrických motorů, zhoršují zřejmě aerodynamické vlastnosti létajících strojů, v jejichž pohonných jednotkách jsou použity, více než vrtule nepohyblivé, neřkuli vrtule sklopné.