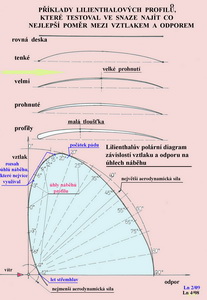
Polára letounu

Nyní, když jsme obeznámeni s odporem, vztlakem, momentem, výslednou aerodynamickou silou a jejich součiniteli a když víme, že jejich velikosti závisí na rozměrech letadla (hlavně křídla), rychlosti letu, poloze (úhlu náběhu) při níž se letoun pohybuje vzduchem a na teplotě a tlaku vzduchu, můžeme sestavit diagram, kde na vodorovnou osu vynášíme součinitelé odporu cx a na osu svislou součinitelé vztlaku cy, příslušející vždy stejným úhlům náběhu. To jako jeden z prvních udělal na konci 19. století neopomenutelný průkopník letectví Němec Otto Lilienthal. Viz následující obrázek.

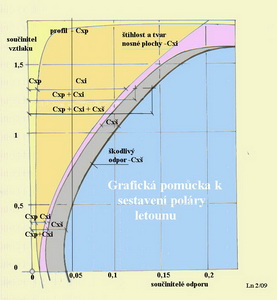
Polára letounu je aerodynamickou charakteristikou křídla, k níž jsou přiřazeny aerodynamické vlivy dalších jeho částí, jimiž je v převážné míře jejich odpor. Jejich součtem je pak křivka, která je od té původní, náležející pouze křídlu, posunutá v souřadných osách, obou prve uvedených součinitelů, vpravo. A sice o hodnotu tak zvaného součinitele škodlivého odporu c_xš.

Jak ji určíme ?

Postup, zase jen zjednodušený a proto jen přibližný, je obdobný jako v případě předchozím, kdy jsme sestrojovali(počítali) poláru křídla z poláry profilu. Začneme s polárou křídla a k ní připojíme ke všem dříve zvoleným hodnotám součinitelů vztlaku hodnoty součinitele prve zmíněného součinitele škodlivého odporu. Do něj započítáváme poměrné odpory všech ostatních částí letadla mimo křídla. Je to - trup, ocasní plochy, podvozek, vyčnívající části motoru, odpor vznikající při průtoku vzduchu chladícími kanály, vrtule, anténa, případná výzbroj přesahující původní obrysy letadla, přídavné nádrže atd.

Hodnoty součinitele škodlivého odporu se mohou nacházet v rozmezí 0,0075 až asi 0,035. Ty nejmenší náleží například velmi dobře zpracovaným návrhům větroňů, které mají velmi hladké a nezvlněné povrchy, bez výčnělků. Ty největší pak motorovým letadlům, jejichž tvary jsou pragmaticky podřízeny jejich poslání, takže se vyznačují liniemi značně vystupujícími ze základního obrysu letadla s mnoha nástavbami a dodatečnými součástmi a jejichž mnohé povrchy nectí příliš zákonitosti zachování co nejmenšího aerodynamického odporu.

Velikost součinitele škodlivého odporu se uplatňuje hlavně při létání vysokými rychlostmi, kdy je jeho hodnota srovnatelná nebo dokonce mnohem vyšší než součinitel odporu samotného křídla. Součinitel indukovaného odporu je při tom zanedbatelný, protože vztlak je velmi nízký. Při létání při větších úhlech náběhu, dejme tomu mezi asi 2 až 15 stupni, je jeho podíl na celkovém součiniteli odporu letadla mnohem menší. Obvykle se se součinitelem škodlivého odporu zachází při konečné kalkulaci poláry letadla tak, že se při menších a středních hodnotách součinitelů vztlaku, které budou hlavně provozně využívány, používá jeho stálá hodnota a teprve při větších úhlech se mírně zvětšuje.

Tento postup je graficky zachycen v následujícím obrázku.

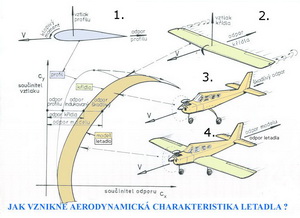
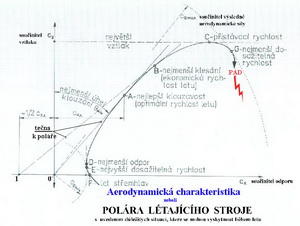
K čemu může být potom takový diagram dobrý, je-li vůbec k něčemu použitelný?

Pokusíme se z něho vytvořit něco užitečného a pro mysl příznivců létání zajímavého. Při troše představivosti, kterou povzbudíme několika obrázky, se nám to u vážných zájemců určitě podaří.

Co jsme schopni z takového diagramu vytěžit a nestát se zapřisáhlými odpůrci trochy zpopularizované teorie. Jak můžeme sami, aniž bychom byli ovlivňováni prodejci letounů, nebo těmi, co tvrdí, že létá všechno, poznat jak se bude letoun, jehož poláru máme, chovat v různých situacích během letu ?

Začněme třeba některými letovými stavy k nimž za letu dochází. V následujících obrázcích jsou uvedeny ty, co se mohou vyskytovat i u malých lehkých letadel.

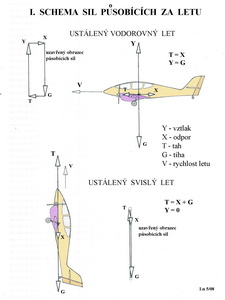
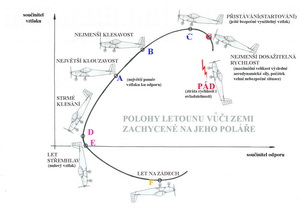
Když například ve stoupání přiměřenou rychlostí letu, chceme dosáhnout stoupavosti jakou potřebujeme (nebo si přejeme), pokud jsme ovšem nepřecenili výkon naší pohonné jednotky, je třeba k tomu připomenout, že tento manévr sestává v podstatě ze dvou pohybů, na něž musíme použít výkon pohonu. Je to překonání celkového odporu letadla, jež odpovídá vodorovnému letu při zvolené rychlosti letu a zároveň jeho zvedání směrem vzhůru (jako ve výtahu). Při zvedání musíme překonávat nejen tíhu letadla, ale i klesavost příslušející dané rychlosti letu. Z toho plyne, že čím vyšší rychlost zvolená pro stoupání, tím větší je nutný výkon pohonné jednotky. Je jen jeden letový stav, při němž je stoupání nejefektivnější a tím je jeho poloha vůči směru letu, kdy je jeho klesavost (zjištěná z poláry) nejmenší. Všechny ostatní jsou energeticky náročnější.

Ve vodorovném letu, jak již zmíněno prve, záleží velmi na zvolené rychlosti letu. Potřebný výkon pohonné jednotky je totiž přímo úměrný její třetí mocnině. Pro názornost přibližme tuto syrovou skutečnost takto : zvýšíme-li (pokud ovšem můžeme) rychlost letu dvakrát potřebujeme k tomu přibližně osmkrát větší výkon. Jedná se samozřejmě o letadlo se stejnými aerodynamickými charakteristikami.

V sestupném letu zase obvykle nepotřebujeme příliš mnoho výkonu z pohonné jednotky, neboť nám zásadně pomáhá zemská přitažlivost. Je třeba dokonce dát si pozor, aby rychlost letu nepřekročila hodnotu, která byla s určitou jistotou ve výpočtu použita pro dimenzování jednotlivých částí letounu. V praxi se například pro hrubou „regulaci“ rychlosti letu ve strmém sestupném letu může, celkem úspěšně, použít výrazné změny otáček motoru. Vrtule se tak stane méně účinnou, její odpor velmi stoupne a dokonce může nabýt záporných hodnot. Tato dodatečná síla pomůže zbrzdit příliš rychlý let. U letadel s aerodynamickými brzdami je třeba jejich použití správně načasovat, aby nedošlo k destrukci těch částí, na nichž jsou připevněny.

V letu střemhlav, kdy je vztlak roven nule, je dosahováno téměř maximální rychlosti letu. Výkon pohonné jednotky není obvykle prakticky využíván a jsou při něm obdobné poměry jak je popsáno v předchozím případě. Nebezpečí destrukce křídla a ocasních ploch je velké a při tomto letovém stavu je třeba respektovat podmínky, pro něž bylo letadlo navrhováno. Piloti by měli být velmi obezřetní jak před započetím tohoto manévru, tak i během jeho průběhu, zejména hodlají-li křivku dráhy letu, nebo polohu letadla výrazněji měnit.

V následujícím obrázku jsou zajímavé letové situace zachyceny.

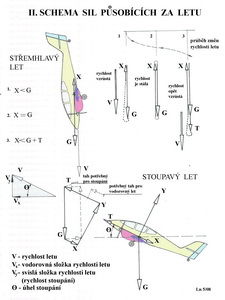
Můžeme procházet celou poláru a určit nebo posoudit letové stavy v celém rozsahu rychlostí od té, kdy letadlo začne již padat – bod G, protože velký úhel náběhu jeho křídla i nízká rychlost letu nestačí zajistit vztlak potřebný pro let, až po rychlost střemhlavého letu – bod E, kdy je na křídle nulový vztlak. Mezi těmito krajními polohami jsou všechny ostatní, při nichž je letadlo možné „provozovat“, pokud nepřekročíme meze namáhání konstrukce a osádky. Jestliže pokračuje letadlo ve změnách úhlů náběhu do dalších záporných hodnot, začne za bodem E přecházet do letu na zádech.

Podívejme se nyní na to jak letadlo mění svoji polohu mezi body G a F a to jednak z pozice pilota a jednak diváka na zemi.

Co by mohl zaznamenat pilot, kdyby chtěl a měl na to čas? Jestliže bude pilotovat letadlo s křídlem jež má profil dejme se 2% prohnutím, bude se toto křídlo v bodě E nacházet vůči směru letu po úhlem cca -2_o. V bodě G to bude naopak úhel kladný o velikosti cca 16_o. Celkový rozdíl úhlů náběhu křídla v rozmezí rychlostí pádu ( bod G ) a rychlostí letu střemhlav (bod E) bude tedy cca 18_o.

Jak to zaznamená divák stojící na zemi? Jestliže je schopen zaznamenat změny úhlů náběhu od asi 3_o může sledovat v podstatě jen postavení trupu letadla vůči zemskému povrchu (horizontu) a podle toho usuzovat na stav letu. Pád, let střemhlav a let na zádech pozná každý. Mezi tím to však není zas tak jednoduché a ani bezpečné.

A jak to vidí nebo spíše cítí pilot? Tomu se v pozici odpovídající části poláry mezi body C a G začne vytrácet horizont, až zmizí úplně a pilot hledí do nebe. Spousta zvuků, zejména u větroňů, utichá, let se zastavuje a pak letoun již jen padá. Nejprve po ocase a pak ve velmi strmém sestupném letu. Rychlost vzrůstá a zem se řítí proti pilotovi vstříc připomínajíc mu nekompromisní působnost zemské přitažlivosti. Na tyto „scenerie“ rychle narůstajících rozměrů předmětů, staveb, stromů, silnic, řek apod. je třeba si případně zvyknout.

Takže pokusíme-li se to shrnout můžeme konstatovat, že křídlo letounu změní mezi body F a G svoji polohu vůči směru letu ve vzduchu o cca 24_o až 27_o. Kdežto trup letounu vůči Zemi asi o 275_o ( při přemetu o celých 360_o). A toho si všimne každý pozornější divák na leteckém dnu, i když ho samotná polára nijak zvlášť nezajímá. Po pravdě řečeno ani neví, že něco takového existuje. Stoupenci létání by však takový nezájem projevovat neměli.

V následujícím obrázku je obdobné připomenutí důležitých letových situací s poněkud odlišným komentářem od obrázku předchozího.

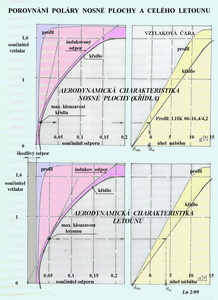
A teď se vraťme k článku v minulém magazínu AL, jmenovitě k motorovému letounu s rozpětím 9,5m a profilem LHK 06-16,4/4,2 , který jsme opustili ve fázi zhotovení poláry jeho nosné plochy a pokusme se sestavit jeho výslednou poláru.

Jak jsme již naznačili v úvodu tohoto článku postačí nyní ke grafickému sestrojení poláry letounu použít poláru jeho nosné plochy a přiřadit k ní odpovídají součinitel škodlivého odporu. Ten volíme pro tento případ v hodnotě 0,02. Je to docela jednoduchý postup, ale výsledky aerodynamických charakteristik se změní významně. Jak může bystrý čtenář vyčíst z následujícího obrázku.

Do jeho horní části je převzata polára křídla letounu, tak jak jsme k ní dospěli minule. V jeho levé části jsou průběhy součinitelů odporu profilu a odporu indukovaného. Jejich součtem je pak součinitel odporu křídla(nosné plochy)- silně vytažená křivka vpravo. Jestliže zavedeme tečnu z počátku souřadnic k této křivce získáme v bodě dotyku součinitele odporu a vztlaku odpovídající maximální klouzavosti neboli nejmenšímu úhlu klouzání. Když se posuneme rovnoběžně s vodorovnou osou do pravého diagramu ke vztlakové čáře křídla a z takto získaného průsečíku spustíme svislici na osu úhlů náběhu, dostaneme se k hodnotě cca -0,4 stupně. To by byl úhel náběhu samotné nosné plochy při němž by mohlo být dosahováno maximální klouzavosti. Pozor: nezaměňovat úhel náběhu s úhlem nastavení nosné plochy na trupu letounu.

V dolní části je stejný grafický zápis jako byl ten předchozí, „pouze“ s tím rozdílem, že počátek souřadnic je jednoduše posunut o hodnotu součinitele škodlivého odporu ( hodnotu 0,02 zde uvažujeme stálou pro celý rozsah součinitelů vztlaku, což sice není zcela správné, ale pro naše zpopularizované výklady to postačí) doleva. A podívejme se co z toho vzniklo. Vedeme-li nyní tečnu z počátku souřadnic k původní poláře křídla-nyní ale posunuté vpravo vlivem součinitele škodlivého odporu, získáme v bodě dotyku úplně jiné hodnoty součinitelů vztlaku a odporu příslušející maximální klouzavosti, tentokrát celého letounu. Úhel klouzání se oproti pouhému křídlu výrazně zvětšil, takže letoun klesá k zemi mnohem rychleji a nedoletí ze stejné výšky tak daleko. Změnil se i tomu odpovídající úhel náběhu letounu a to na hodnotu cca 4 stupně.

Takhle nějak to dopadne vždycky, když se kdokoliv rozhodne začít navrhovat létající stroj s pevným křídlem. Původní vysněná přání, když si myslíme, že máme nejskvělejší profil jaký lze opatřit, se postupně rozplývají až je nutné se smířit s výsledkem, jehož jsme dosáhli například, v našem magazínu, uvedeným způsobem.

A přesto nakonec ještě jedno opakování pomocí grafické pomůcky zachycené v následujícím obrázku.

V něm je uveden jeden z možných postupů grafického sestrojení poláry celého letounu. Ve známém souřadném systému svislé osy součinitelů vztlaku a vodorovné osy součinitelů odporu vyneseme průběh poláry profilu, tak jak jsme jej získali předminule.K němu přidáme průběh součinitele indukovaného odporu cxi. Součtem součinitelů odporu profilu a indukovaného odporu získáme poláru nosné plochy. Povšimněte si znovu jak její tvar ovlivnil zejména průběh indukovaného odporu a jak se její vrchol snížil (vlivem působení cirkulace kolem profilu).

To všechno vyhotovujeme vždy pro stejnou hodnotu součinitele vztlaku, jak jsme poznali minule. Nyní přidáme k tomuto grafickému zápisu(poláře nosné plochy) ještě hodnoty součinitele škodlivého odporu cxš. Předchozí křivka se posune o hodnotu 0,02 doprava, tj. do oblasti větších odporů. Je to ta nejsilněji vytažená čára vpravo. A to je polára celého letounu sestavená pomocí zjednodušené metody, která nám, při zde uplatňované úrovni poznávání, postačí.

Když se podíváte do místa se součinitelem vztlaku s hodnotou cca 1,3 a porovnáte velikosti všech tří součinitelů odporu tak poznáte, že výkony letounu nosné plochy daného tvaru a velikosti ovlivňuje nejvíce součinitel indukovaného odporu cxi.

Jestliže se, ale budete posouvat po poláře dolů tak snadno zjistíte, že se vliv jednotlivých součinitelů odporu na výkony letounu mění zásadně. O tom podává důkaz uvedený příklad pro součinitel vztlaku cca 0,35. Zde má největší vliv součinitel škodlivého odporu a teprve po něm součinitel indukovaného odporu. Z toho lze usuzovat na to, že při vyšších rychlostech létání ovlivňují výkony letounu všechny ostatní jeho části stále více než profil a tvar a velikost nosné plochy.

Při nulovém součiniteli vztlaku, let střemhlav, začíná vedle indukovaného odporu nabývat většího vlivu, než tomu bylo před tím, i odpor profilu. Indukovaný odpor, protože zmizel vztlak, zde také nepůsobí.

To jsou poznatky zásadního významu, které by měly být uplatněny při navrhování jakéhokoliv létajícího stroje s pevným křídlem.

A ještě opravdu poslední poznámka o tom, že není všechno zase tak úplně jednoduché. Prostý algebraický součet všech součinitelů odporu je nutno, s ohledem na vzájemné ovlivňování se všech částí letounu, ještě vynásobit obvykle násobkem větším než 1. Takže se polára letounu posune znovu o trochu více vpravo a zaznamená tak další zhoršení výkonů. Pro úplnost je třeba říci, že hodnota uvedeného násobku bývá někdy i nepatrně menší než 1, ale to bychom doporučovali ponechat nepovšimnuto v rámci početních postupů. Obvykle má násobek, zvětšující součet odporů, hodnotu v rozmezí cca 1,03 až 1,15.

Tím nyní končíme povídání o polárách letounů s pevnými křídly. Ne však o všech, jak poznáte příště.