O některých momentech
provázejících létající stroje

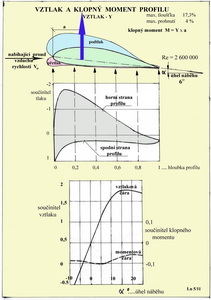
O některých věcech je třeba mluvit častěji, než by se zdálo již jenom proto, že nově přicházející adepti letectví, nemluvě ani o mnoha současných, nebyli s tím souvisejícími informacemi dotčeni. Tentokrát to bude populárně o momentech provázejících létání k tomu určených strojů neboli letounů i jejich modelů.

Síly působící na letoun jednak mění svoje velikosti a jednak se nacházejí na jeho různých místech a proto vyvolávají různé momenty k jeho těžišti. To jsme již naznačili v dřívějších magazínech několikrát.

V rovnovážném letu musí být nejen všechny síly, ale i momenty působící na letoun v rovnováze.

Moment, obecně řečeno, vzniká působením síly na nějakém rameni, které vztahujeme u letounů převážně k jeho těžišti. Pokud se jedná o nosnou nebo ocasní plochu pak je to její hloubka.

Jak to asi vypadá na profilu jestliže je obtékán proudem vzduchu o rychlosti Vo je zachyceno v prvním obrázku.

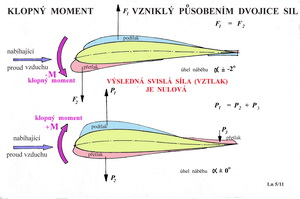
Vztlak, který je výslednicí podtlaku nad profilem a přetlaku pod ním působí na nějakém rameni, například k jeho náběžnému bodu a snaží se profil(křídlo nekonečného rozpětí) překlopit. Tak vzniká klopný moment.

Vztlak nemá však na profilu stálé působiště. S rostoucím úhlem náběhu se pohybuje směrem k náběžné hraně a naopak a proto je jím vytvářený klopný moment proměnný. Bez dalších zdůvodnění konstatujme, že na profilu existuje bod nacházející se přibližně v jedné čtvrtině jeho hloubky, nám již dobře známý aerodynamický střed profilu, k němuž je v určitém rozsahu úhlů náběhu( kdy ještě nedochází k velkým deformacím proudění kolem profilu) tento moment přibližně stálý.

V tomto obrázku je v horní části zakreslen přibližný průběh rozložení tlaků podél hloubky profilu na jeho horní a spodní straně. Pod ním je uveden průběh tlakového součinitele pro stejné podmínky. Ve spodní části jsou pak uvedeny závislosti součinitele vztlaku a klopného momentu na úhlu náběhu profilu. Z těchto údajů je pak, mimo jiné, možné stanovit jak se síly tlaku snaží profilem klopit, tj. otočit jím ve směru hodinových ručiček nebo proti němu.

Zvláštním, ale velmi známým je případ působení dvojice sil stejné velikosti a opačného smyslu. Viz následující obrázek.

Jedná se o obtékání prohnutých profilů se záporným nebo velmi malým úhlem náběhu, při němž je výsledná vztlaková síla rovna nule (ne ale odpor). Výsledkem tohoto silového působení pak je pouze moment snažící se profil (nosnou plochu) natočit(klopit) buď proti smyslu hodinových ručiček ( jednoduše prohnuté profily) nebo v jejich smyslu (dvojitě prohnuté tzv. „autostabilní“ profily). Takto vzniklý moment se snaží klopit letoun jeho přídí dolů ( značený záporným znaménkem) nebo nahoru ( s kladným znaménkem). To již ale známe z dřívějších našich textů. Jen to zde pro úplnost připomínáme.

V různých letových situacích lze dosáhnout původní nebo nové rovnováhy všech působících sil a momentů tím, že využijeme například sil a momentů vznikajících pomocí systémů řízení na ovladatelných částech nosné plochy (křidélka, klapky, spoilery) a ocasních plochách (výškové a směrové kormidlo).

Jedná se například o situace, kdy na letoun zapůsobí vnější vlivy – poryvy větru nebo nevhodně zaujmuté letové polohy porušující rovnovážné stavy – let při velkém úhlu náběhu nebo s velkým vybočením, strmý sestupný let nebo jiné akrobatické obraty apod.

Vezměme ku pomoci následující obrázek.

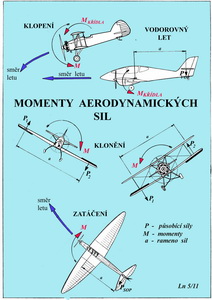
O působení klopného momentu, který jsme se snažili v předchozím textu znovu připomenout, vypovídají obě horní schemata tohoto obrázku.

Levé schema představuje situaci, kdy klopný moment nosné plochy (křídel) není vyrovnáván žádnou další sílou působící na vhodném rameni. Letoun se může pohybovat po strmé sestupné dráze až přejde do polohy letu „na zádech“. Ten však netrvá dlouho a stroj se v nekontrolovaném letu zřítí na Zem. Taková je nejen teorie, ale i praxe, když letící stroj přijde o VOP. Některým modelům se to stává a následuje pohyb k Zemi popsaný prve. Takhle se ale vzduchem pohybovat nechceme.

Druhé schema podává obraz toho jak VOP a na ni vzniklý vztlak působící na rameni a dokáže eliminovat klopný moment nosné plochy. Je to docela prostá rovnováha dvou momentů jak může každý pochopit. A takto působí síly na pohybujícím se letounu. Vztlak nosné plochy i VOP, stejně tak jako klopný moment, mohou působit ale i opačně.

Oba tyto příklady souvisely s rovnováhou stroje podél příčné osy (viz trojrozměrnou aerodynamickou soustavu ve „Sborníku vybraných výrazů“) klopením.

Pohyby kolem podélné osy letounu jsou zvány kloněním. V těchto případech je po předchozím porušením letu dosahováno původní nebo nové rovnováhy letu například působením křidélek. Obě (předpokládáme, že obvykle funguje na každé polovině křídla jedno křidélko, což ale nemusí být vždy zajištěno) křidélka jsou při tom nesouhlasně vychýlena. Tím je porušena předchozí fáze letu tím, že na každé polovině křídla vznikne jiná aerodynamická síla (geometrický součet vztlaku a odporu). Tento stav je podobný působení dvojice sil(ty však ale nemusí být stejně velké) a snaží se letoun navrátit do původní polohy(pokud o to pilot stojí) nebo tuto, obvykle, nerovnovážnou, polohu ještě jinak změnit. To je na obou prostředních schematech zachyceno.

Tento pohyb je možné ještě ovlivňovat(pokud k tomu jsou dostatečné možnosti) výchylkami výškového kormidla a pak je možné v náklonu stoupat či klesat nebo letět v horizontu.

Někdy, pokud má nosná plocha nějaké vhodné vzepětí, je možné ovládat příčné náklony i jen pouhou SOP. Týká se to však převážně jen modelů letadel.

A spodní schema ukazuje možnost jak ovlivňovat výchylkami směrového kormidla pohyby kolem svislé osy letounu, zvaná zatáčení. Síla vzniklá na SOP začne letounem zatáčet vlevo nebo vpravo, podle výchylky směrového kormidla na rameni a , což je jeho vzdálenost od těžiště a vytvoří tak zatáčivý moment, který uvede letoun na jinou než přímou dráhu. Jestliže je výchylka směrového kormidla, vůči velikosti a tvaru vzepětí, nevhodně veliká přejde letoun po poměrně krátké době do strmého sestupného letu. V tomto stavu je nutné využít funkce křidélek k nápravě porušené rovnováhy nebo opačné výchylky směrového kormidla, což využívají často modely letadel.

To bylo připomenutí některých momentů vyskytujících se na pohybujícím se letounu, jež byly výsledkem aerodynamických sil vzniklých na jeho nosných a ocasních plochách.

Jsou tu ještě další momenty vyskytující se na nosných a ocasních plochách pokud jsou tyto opatřeny pohyblivými plochami-kormidly. Ta jsou otočná kolem vhodné osy, mají nějakou plochu a vykazují oboustranné výchylky ve vhodném rozmezí úhlů.

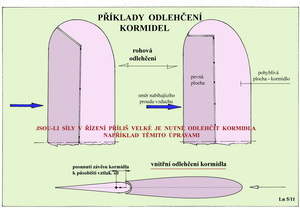
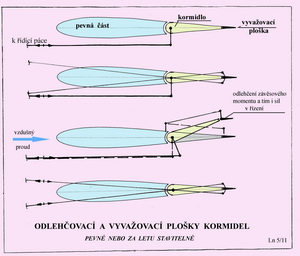
V přední, obvykle větší, části plochy je část pevná a na ní je otočně upevněna část pohyblivá. Jestliže je pohyblivá část v neutrální poloze – její výchylka je nulová (viz horní část obrázku), pak se obvykle další síly, vyjma odporu, na ní nevyskytují.

Jestliže se ale ze své neutrální polohy vychýlí vznikne další síla, kterou můžeme popsat jako vztlak (i když působí například na SOP převážně vodorovně). Tato síla se snaží vychýlit letoun z původní dráhy letu. To ví skoro každý z vlastní nebo zprostředkované zkušenosti.

Při tom však na otočné závěsy kormidla začne působit ještě moment (viz spodní část obrázku), jehož velikost je určena součinem síly vzniklé na kormidle a její vzdálenosti od středu otáčení. To je tak zvaný závěsový moment. Síla vzniklá na ploše vlivem výchylky jejího kormidla (křidélka) se přenáší soustavou řízení až k pilotovi ( u modelu letadla k servopohonu). Tyto síly mohou dosahovat značných hodnot, jež pilota unavují nebo je v krajních případech není schopen zvládnout vůbec. U modelů letadel mohou vést snadno ke zničení převodů servomechanismů.

V praxi se proto postupuje například tak jak ukazuje další obrázek.

Okraje ocasních nebo nosných ploch jsou upraveny tak, aby pohyblivé části v těchto místech přesahovaly před osy otáčení. Tyto části pak vykazují při vychýlení kormidla opačně působící vztlakové síly ve srovnání s ostatní plochou kormidla a zmenšují tak závěsový moment a tím i výsledné síly v řízení. Je to způsob rohového odlehčení kormidla, který je známý dlouhou dobu.

Ve spodní části tohoto obrázku je příklad jiného řešení vedoucího ke zmenšení účinků závěsového momentu kormidla. Osa otáčení kormidla je posunuta blíže k působišti jeho vztlakových sil. Tím se zmenší rameno na němž síla působí a závěsný moment se proto také zmenší. Je to tzv. vnitřní odlehčení kormidla.

Ještě je třeba poznamenat, že úplné odstranění účinků závěsných momentů není žádoucí. Síly v řízení by se mohly případně zmenšit tak, že by jednak neupozorňovaly pilota na jejich stav a hlavně by nevracely kormidla do neutrálních poloh v případě uvolnění řídící páky dostatečně rychle a spolehlivě.

Následující obrázek přibližuje příklady použití a funkce tzv. vyvažovacích či odlehčovacích plošek umístěných v zadních částech a to obvykle jen na částech rozpětí kormidel. Jejich cílem je jednak vymezit účinky závěsových momentů kormidel a také umožnit trvalejší vyvážení rovnováhy letu, aby pilot nebyl nucen během letu neustále působit na řídící systém ( páky, pedály,..), pokud nemá automat.

V horní části obrázku by to mohl být případ vyvažovací plošky pevně nastavitelné na Zemi, jejíž výchylka je trvale nastavena tak, aby kompenzovala nebo úplně odstranila účinky jiných sil, například na SOP od vrtulového proudu nebo na VOP při nevhodně zvoleném úhlu seřízení VOP a nosné plochy a podobně.

Druhý příklad z obrázku představuje schema řešení vyvažovací plošky ovládané během letu pomocí řídících mechanizmů.

Další dvě řešení uvádějí schema řešení pro odlehčení závěsového momentu v návaznosti na výchylku kormidla.

Je vhodné si uvědomit, že jiným nastavením řídící páky aerodynamického vyvážení, to byly všechny předchozí řešení ovlivňující velikost závěsových momentů, se nemění síly nastávající při vychylování kormidel.

Ještě upozorníme na hmotové vyvážení kormidel. Oč se jedná?

Kormidla mají obvykle vlastní hmotové těžiště za osou otáčení, takže při neustálených stavech na něm vznikají vedle aerodynamických i síly setrvačné, které vyvolávají nežádoucí momenty a z toho plynoucí nechtěné výchylky kormidla. To se vedle nežádoucích průběhů závěsových momentů mnohdy projeví i tak, že dochází k třepotání kormidel, což je jev velmi nebezpečný. Zkoumání tohoto jevu souvisí s disciplínou zvanou aeroelasticita. Těmto nežádoucím efektům se předchází umístěním přídavných závaží uvnitř i vně předních částí tak, aby se hmotové těžiště kormidla přiblížilo ose jeho otáčení.

V následujících obrázcích jsou uvedeny příklady skutečných rohových odlehčení kormidel, jejich vyvažovacích - odlehčovacích plošek a hmotová vyvážení kormidel.

A teď něco o momentech, jejichž příčinou jsou rotační části pohonných jednotek, tj. vrtule, rotory motorů i dmychadel. To jsou všechno setrvačníky, které ovlivňují pohyb letounů nejen s pevnými křídly. Na pořadu je proto populárně podané vysvětlení jejich působení. Jedná se o jimi způsobený reakční a gyroskopický moment.

Pro co nejjednodušší vysvětlení použijeme opět grafické vyjádření okolností, které to provázejí.

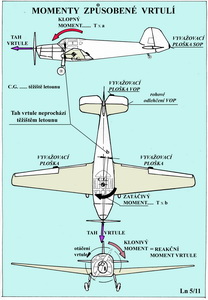
V tomto obrázku jsou schematicky zachyceny případy vlivu rotující vrtule na pohyby letounu a také příklad rozmístění pevných, na Zemi stavitelných, vyvažovacích plošek na letounu. Je tu také příklad rohového odlehčení výškového kormidla.

Na rotující vrtuli vzniká vedle hluku a vibrací i síla, kvůli které je vrtule na letoun instalovaná, zvaná tah a také reakční moment o který však nijak nestojíme (podle 3. Newtonova zákona – principu akce a reakce).

V horní části obrázku je příklad, kdy tah vrtule míjí těžiště letounu (měřeno ve svislé rovině) a vytváří tak klopný moment, v tomto případě „těžký na hlavu“. Čím větší je rameno tahu vůči těžišti a čím větší je tah, tím větší je i z toho vzniklý klopný moment.

Ve střední části obrázku je příklad, kdy tah vrtulové pohonné jednotky také neprochází těžištěm (zjišťováno ve vodorovné rovině) a vytváří tak zatáčivý moment na letounu.

Ve spodní části je pohled zepředu na letoun s rotující vrtulí, kdy vzniklý reakční moment všech rotujících částí pohonné jednotky se snaží letoun naklonit ve smyslu proti smyslu rotace. Čím jsou hmotnosti rotujících částí větší a čím je změna jejich otáček prudší, tím je reakční moment větší. To lze snadno poznat při zapnutí nebo vypnutí motoru. Stejně tak jako při náhlém zvýšení výkonu jednotky za letu s hmotnější vrtulí velkého průměru. Při startu mohou v takovýchto případech nastat vážné potíže.

Pro docílení přímého, nebo jemu velmi blízkého tvaru, letu se často kompenzuje vliv reakčního momentu rotujících částí pohonné jednotky vyosením osy rotace ve vodorovném směru (viz střední část obrázku),takže proti sobě působí zatáčivý moment tahu a klonivý moment způsobený reakčním momentem rotujících hmot.

U letounů s několika pohonnými jednotkami je nutno všechny tyto vlivy zohlednit podrobněji a navíc ještě posoudit možné vlivy vrtulových proudů na jeho jednotlivé části nebo jeho modelu.

Následuje ještě jeden obrázek na němž je schema působení vrtule a dalších rotujících částí pohonné jednotky na pohyb letounu. Tyto rotující hmoty se chovají jako setrvačník a pokud se letoun pohybuje přímočaře nebo se otáčí kolem své podélné osy, žádné další účinky se jejich působením nevyskytují (vyjma setrvačných sil ostatních částí letounu). Prve jsme ale připomenuli reakční moment rotující částí pohonné jednotky.

Jiné situace nastávají, jestliže letoun zatáčí nebo stoupá či klesá nebo vykonává všeliké akrobatické obraty. V následujícím obrázku je učiněn pokus tyto jevy velmi zjednodušeně a populárně vysvětlit.

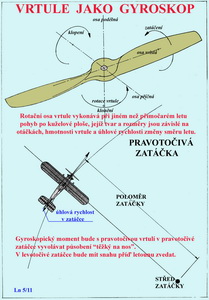
V horní části obrázku je připomenutí tzv. precesního pohybu setrvačníku, v našem případě rotující vrtule, jenž je podepřen v ose rotace pod rovinou otáčení. Může to být vzdálenost vrtule od těžiště letounu. V tomto případě jakýkoliv vnější podnět, snažící se změnit původní osu rotace vrtule, má za následek změnu jejího pohybu, která nyní opisuje kuželovou plochu. Dále to nebudeme rozvádět. Uvedeme pouze Žukovského pravidlo: je-li setrvačník nucen vykonávat precesní pohyb, pak se vzniklý gyroskopický moment snaží natočit osu rotace setrvačníku do směru osy nuceného pohybu.

Ve spodní části obrázku je příklad letounu s pravotočivou vrtulí zatáčejícího vpravo. Letoun tímto manévrem nutí konat rotační osu vrtule precesní pohyb. Reakcí setrvačníku = vrtule + další rotující části pohonné jednotky, vzniká reakční silová dvojice. Této reakční dvojici říkáme gyroskopický moment. Ten se pak snaží natočit letoun podle jedné ze dvou dalších volných os. V tomto případě kolem příčné osy letounu, při čemž je jeho smysl „těžký na hlavu“. Jestliže by letoun konal zatáčku vlevo pak by vznikl gyroskopický moment ve smyslu „těžký na ocas“.

Jiný příklad : při rozjezdu letounu s ostruhovým kolem vznikne při zvedání jeho zadní části trupu s ocasními plochami také gyroskopický moment kolem osy svislé.

Pro snazší pochopení účinků gyroskopických momentů uveďme jeden konkrétní příklad jeho výpočtu pro letoun konající pravotočivou zatáčku o poloměru 280 m, rychlostí 450 km/h, jehož rotační části pohonné jednotky mají moment setrvačnosti 25 kgm2 a vrtule se otáčí 2 400 krát za minutu. Po krátkém výpočtu, který si odpustíme, zjistíme, že výsledný gyroskopický moment působí na letoun v této letové situaci velikostí 2 805 Nm a to ve smyslu „těžký na hlavu“.

Vypůjčil jsem si tento příklad ze zdroje: Bohumil Vybíral-Setrvačníky a jejich aplikace.

Modeláři mohou snadno poznat účinky reakčního i gyroskopického momentu mají-li k dispozici trup modelu s rotující vrtulí. Stačí pozorně sledovat reakci trupu při spuštění motoru a pak při jeho vypnutí a také při pohybech ve vodorovné a svislé rovině. Účinky obou momentů jsou při těchto demonstračních testech „hmatatelné“.

Vedle momentů připomenutých v tomto článku existují ještě další, které provázejí létající stroje. O těch se můžeme zmínit v případech, kdy na ně narazíme, pokud jsme tak již neučinili někdy dříve.