 Vznášení, vzácní páni, není létání. Je to jen jakési toulání atmosférou Země a to víceméně na základě její libovůle. I když ta je rozmarná, nachází se na Zemi již asi 320 let, obrovské množství těch, kteří tento způsob pohybu v atmosféře vyznávají. Pomocí čeho se toulají vzduchem mezi nebem a Zemí?
Vznášení, vzácní páni, není létání. Je to jen jakési toulání atmosférou Země a to víceméně na základě její libovůle. I když ta je rozmarná, nachází se na Zemi již asi 320 let, obrovské množství těch, kteří tento způsob pohybu v atmosféře vyznávají. Pomocí čeho se toulají vzduchem mezi nebem a Zemí?
Jsou to balony plněné látkou lehčí než okolní vzduch a pak také jejich příbuzné – vzducholodě, které mají možnost díky pohonné jednotce ještě plout, tak trochu, kam se jim zamane. Zůstaňme však dnes jen u balonů a u toho co jim umožňuje plout a vznášet se stovky metrů i desítky kilometrů nad Zemí.
Oč se jedná????
Je to pouhá praktická aplikace Archimedova zákona, jenž vyhodnotil před drahnou dobou to, že všechna tělesa ponořená do tekutiny jsou v ní nadlehčována silou rovnající se tíze tekutiny objemem tělesa vytlačené. S tím se setkal každý, kdo se alespoň pokoušel plavat nebo brodit vodou. Stavitelé lodí o tom vědí své. Stavitelé vzdušných lodí – balonů a vzducholodí také. Podívejme se na to trochu blíže. V podstatě to bude jen opakování toho co jsme si měli zapamatovat ze školy.
Síla, kterou je uzavřené těleso nadlehčováno v tekutině (kapalině či plynu) je nazývána u balonů a vzducholodí nosností. Mohli bychom to popsat zjednodušeně třeba tak, že její velikost se rovná rozdílu mezi tíhou plynu v balonu a tíhou jím vytlačeného vzduchu. Takže z toho vyplývá, že nosnost balonu bude tím větší čím větší bude rozdíl měrných vah plynu v balonu a okolním vzduchem a také čím větší bude objem balonu. Plyny jsou od sebe odděleny pokud možno neprodyšnou a pevnou elastickou tkaninou, která případně umožňuje měnit poněkud objem balonu, neboť tlaku v atmosféře s výškou ubývá a plyn uvnitř balonu se rozpíná.
Pro bližší pochopení tohoto poněkud jiného výkladu Archimedova zákona použijme dva extrémní příklady:
-jestliže bude v balonu vzduch stejné teploty a tlaku jako má vzduch okolní nebude mít takovýto vzduchoplavecký prostředek žádnou nosnost neboť všechny síly působící uvnitř i vně balonu budou vyrovnány (mimo tíhy balonu)
-jestliže však bude v balonu vzduchoprázdno (vakuum) pak bude jeden metr krychlový jeho objemu vykazovat nosnost asi 12,2 N při teplotě 15 stupňů Celsia a u nás obvyklém atmosférickém tlaku při Zemi. Bylo by sice poněkud méně snadné zhotovit takovou nádobu odolávající vnějšímu přetlaku, ale nebylo by to nemožné
-když však naplníme balon plynem, který bude mít měrnou tíhu menší než okolní vzduch, pak bude mít snahu stoupat(podobně jako bublinky kysličníku uhličitého v sycených nápojích) a při dostatečném objemu balonu ho dokonce zvedat vzhůru.
K plnění balonů, jejichž obal sestává například z polyesterové hedvábné tkaniny s vetkanou zpevňující mřížkou opatřenou akrylátovou nebo polyuretanovou folií, je pak možno použít :
| plyn |
výbušný vodík |
netečné, ale drahé helium |
výbušný svítiplyn |
horký vzduch |
| nosnost 1 m³ plynu v kg |
1,14 |
1,05 |
0,63 |
0,17 – 0,23 |
Vzduch je obvykle ohříván na teploty mezi 80 a 100 °C.
Z této tabulky je patrné, že vzduch má sice nosnost nejmenší, ale zato je nejlevnější a nejbezpečnější (odmyslíme-li si láhve s propan-butanem pro jeho ohřívání).
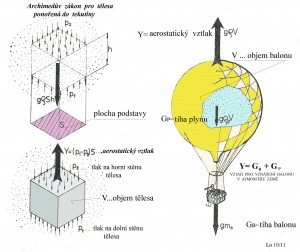
Podívejte se na následující obrázek kde je učiněn pokus graficky znázornit Archimedův zákon a silové poměry na balonu.
Balon o nějaké hmotnosti mB a objemu V je naplněn plynem o měrné hmotnosti ρp .
Na balon působí aerostatický vztlak o velikosti Y=g ρ V , kde ρ je měrná hmotnost vzduchu.
Rovnováha pro vznášení balonu nastane při rovnosti všech působících sil, jak je to uvedeno v obrázku. Z ní je pak možné spočítat hmotnost vznášejícího se balonu mB0 = ( ρo – ρpo ) V.
Výraz v závorce udává hmotnost jakou unese 1 m³ objemu balonu. To jsou ty údaje z předchozí tabulky.
Uvedeme jednoduchý příklad posouzení balonu o maximálním objemu V = 5 m³ , jehož hmotnost je 2,5 kg. Obal balonu je na Zemi naplněn vodíkem s měrnou hmotností 0,09 kg/m³ do objemu jen V = 3 m³ . Po úplném naplnění balonu ve větší výšce, kde je menší tlak, může vodík unikat otvorem ve spodní části volně do atmosféry. Předpokládáme, že balon stoupá jen tak rychle, že se teploty vodíku rovnají teplotám okolí a že není ohříván ani slunečním zářením.
Měrná hmotnost plynu bude se stoupající výškou klesat stejně jako měrná hmotnost okolního vzduchu. Objem balonu se však bude zvětšovat až do jeho úplného naplnění (5 m³ ). Ve větších výškách se však již měnit nebude.
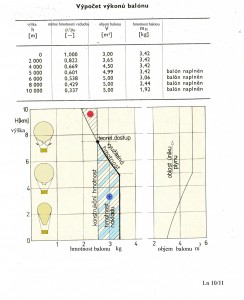
Výšku úplného naplnění balonu zjistíme ze zadaného ( nenaplněného) objemu na zemi V ku maximálnímu objemu V porovnáním s odpovídajícím poměrem měrných hmotností vzduchu v charakteristikách standardní atmosféry ρ /ρ . Takže obdržíme hodnotu 3/5 = 0,6 . Tomu odpovídá podle tabulky u následujícího obrázku výška 5 000 m. V této výšce bude tedy balon naplněn. ³
Jak můžemě spočítat dostup balonu?!
Balon se bude právě vznášet vždy jen při určité celkové hmotnosti. Ta bude například u Země
mBo = ( ρo – ρpo ). Vo = ( 1,23 – 0,09). 3 = 3.42 kg
V libovolné výšce pak musí, po zjednodušení, platit, že
mB = mBo . ρ/ρo . V / Vo
Balon tedy bude stoupat až do výšky 5 000 m, protože jeho nosnost je větší než hmotnost při vypuštění na Zemi a jeho objem se bude při tom zvětšovat až do V = 5 m³.
Podle předchozího výrazu může stoupat tak dlouho až se hodnota ρ ⁄ ρ bude rovnat témuž výrazu odpovídajícímu poměrům v dané výšce, takže to bude
ρ⁄ρo = 2.5/3,42 . 3/5 = 0,438
a této hodnotě, z prve uvedené tabulky, odpovídá maximálně možná dosažitelná výška balonu ( jeho teoretický dostup ), kolem 7 500 m. A v ní by se měl balon vznášet.
Výš však již nevystoupí, pokud ovšem nedojde k nějakému vzestupnému proudění okolního vzduchu.
Na připojeném obrázku a tabulce je celý postup výpočtu uveden.
Pokládali jsme za zajímavé pro naše příznivce uvést tento jednoduchý příklad a také výklad toho jak se tělesa lehčí vzduchu v něm mohou vznášet. Když jsme již před tím upozornili na dva úspěšné pokusy těchto letadel a jejich modelů dosažených u nás v roce 2011.
Balony, ať již plněné jakýmkoliv vhodným plynem, nemají jinou možnost pro volbu směru letu než změnu výšky, kde proudí vzduch jiným směrem. Jinak by musely být vybaveny nějakou pohonnou jednotkou. čemuž zase nesvědčí jejich tvar. Přesto byly některé pokusy v minulosti uskutečněny.
Logickým vyústěním z této situace byl vznik vzducholodí, které svým podlouhlým, víceméně aerodynamickým tvarem umožnily, společně s dostatečně dimenzovanými pohonnými jednotkami, pohyb požadovaným směrem. První úspěšnější pokusy byly vykonány již v 19. století. Nejznámějšími výtvory pak byly stroje Zeppelinovy.
Dnešní nejnovější projekty vzducholodí jsou koncipovány tak, že jejich aerostatický vztlak je o něco menší než jejich letová hmotnost a potřebný zbývající přírůstek vztlaku je zajišťován přiměřeně velkými nosnými plochami – křídly, stejně jako u letounů. Pohonné jednotky mají možnost měnit směr tahu vychylováním do svislé polohy, kvůli zkrácení délky startu. Jsou to tedy jakési hybridy aerostatů a aerodynů.
Teď už jen krátce na závěr trochu úřední řeči:
Letadlo je zařízení, které je schopné udržovat se v atmosféře působením vzdušných sil.
Letadla se dělí na : lehčí vzduchu – bezmotorová…..balony
– motorová……….vzducholodě
těžší vzduchu – z nich nejrozšířenější je letoun.
Balony jsou pak jako letadla lehčí vzduchu zařazeny
v nomenklatuře FAI ve třídách:
plynové …………………….. tř. AA s objemy 250 až 22 000 m³
horkovzdušné ……………. tř. AX se stejnými objemy.
28.10.2011 © Jaroslav Lněnička

Dobrý den, bylo by prosím možné uvést zdroje tohoto článku, zejména zdroje obrázků? Děkuji Novák
Milý hochu,
zdrojů bylo více z různých pramenů a také z mojí hlavy, co si ještě občas pamatuji.
Snad by se dalo něco najít například v knížce z roku 1977 -B.Hoření, J.Lněnička :Letecké modelářství a aerodynamika na stranách 43 až 50.
J.Lněnička
Velice Vám děkuji za odpověď. Novák
Dobrý den, pane Lněničko.
Omlouvám se za svou připomínku k Vašemu dílu seriálu o létání v RC revue 1/2017. Obrázek 1011 je samozřejmě správný, jen by si snad zasloužil trochu vysvětlení textem. Teprve, když jsem spočítal tlakové poměry ve standardní atmosféře jsem zjistil pro mě neuvěřitelnou věc. Na metrovou krychli skutečně shora působí síla o 12 N menší, než na spodní stranu. To přesně odpovídá tíze vytlačeného vzduchu a tak je všechno v pořádku. Člověk si neuvědomuje, že síla atmosférického tlaku je 10 tun na m^2. Přeji Vám hodně zdraví. PS
Jsem rád, milý hochu, že jsme si porozuměli.
Díky za připomínky.
Seriál v RC R již skončil, protože čtenáři byli, podle mě již trochu přesyceni těmi mými povídáními.
S pozdravem
J. Lněnička