 Jak to může být s tahem pohonné vrtulové jednotky během letu v porovnání s jejím statickým tahem, který bývá velmi často předmětem diskuzí. Tahem vrtulové pohonné jednotky zde rozumíme sílu, kterou je tato jednotka schopna vyvinout. Tato síla nemá stálou velikost, protože na ni mají vliv například – průměr a stoupání vrtule, její otáčky, a účinnost , rychlost letu, tvar a počet listů a použité profily vrtule atd. Já ji však v tomto příspěvku použiji, ač ne úplně správně, ke zjednodušenému výkladu o tom, jak se statický tah může přeměňovat v tah potřebný a ještě využitelný.
Jak to může být s tahem pohonné vrtulové jednotky během letu v porovnání s jejím statickým tahem, který bývá velmi často předmětem diskuzí. Tahem vrtulové pohonné jednotky zde rozumíme sílu, kterou je tato jednotka schopna vyvinout. Tato síla nemá stálou velikost, protože na ni mají vliv například – průměr a stoupání vrtule, její otáčky, a účinnost , rychlost letu, tvar a počet listů a použité profily vrtule atd. Já ji však v tomto příspěvku použiji, ač ne úplně správně, ke zjednodušenému výkladu o tom, jak se statický tah může přeměňovat v tah potřebný a ještě využitelný.
Upozorňuji, že jsem na rozdíl od naší společné publikace s Bohouškem Hořením – „Letecké modelářství a aerodynamika“ z roku 1977 (str. 207 a 208), v tomto článku poněkud pozměnil vzájemné vztahy mezi tahem potřebným a tahem použitelným, když jsem je doplnil výrazem tah celkový. Ten je tady součtem obou částí síly zvané tah. Tu je možno měnit během letu například změnou otáček vrtule nebo změnou jejího stoupání.
Pokusil jsem se znázornit na jednom z připojených obrázků, jak se asi může vzájemný poměr potřebného a ještě využitelného tahu měnit v závislosti na rychlosti pohybu letounu a tedy i jeho pohonné jednotky. Vrtule je pevná, to jest bez možnosti změn úhlů nastavení jejich listů.
Je to jen jakýsi demonstrativní pokus jak jinak přiblížit to co je možné očekávat, jestliže máme k dispozici údaj o statickém tahu a chtěli bychom, po čemž mnoho stoupenců letectví touží, z něj získat napříkla údaje o tom jak asi nejrychleji ten stroj s takovou pohonnou jednotkou poletí. Je to jen velmi přibližné poukázání na to co by se mohlo ze statického tahu získat.
I přes očekávanou nelibost, těch co se snaží ledacos nepatřičně zjednodušovat i těch co o tom již něco vědí, chci připomenout, že jsou to údaje jen velmi přibližné, protože se počínaje motorovou zkouškou (statický tah) a dosažením nejvyšší možné rychloti letu mění nejen úhly náběhu listů vrtule, ale i jejich obtékání a tím přirozeně i tah a moment, který musí být schopen motor překonávat. A pak je tu ještě potřeba znát celkový součinitel odporu letounu (tedy i jeho modelu), abychom se dobrali nějaké přibližné hodnoty průběhů rychlostí letu.
Přesto by to nemuselo alespoň některé mudrlanty odradit od pochopení toho o čem bude řeč.
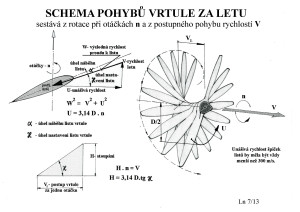
Jak si asi počíná vrtule během letu je zachyceno v následujícím, již několikrát dříve uvedeném, obrázku.
Z něho je možné pochytit některé dost zajímavé (důležité) informace. Například to, že při měření úhlu nastavení listu na zvoleném poloměru, pokud chceme získat jednoduchým přepočtem velikost místního stoupání, získáme součet úhlu nastavení a úhlu náběhu. Úhel náběhu, pokud se nejedná o list s proměnným stoupáním, by se pak mohl nacházet v rozmezí 3 – 5 stupňů po celé délce listu. Což záleží mimo jiné také na použitém profilu listu.
Stoupání vrtule H pak lze spočítat ze vztahu uvedeného dole uprostřed.
Nebo je tu připomenutí, že by unášivá rychlost špiček listu U měla být menší než 300 m/s, a možná jen asi 270 m/s, aby nedocházelo k překročení rychlosti zvuku. I když místní rychlosti na profilech špiček listů mohou této hodnoty dosáhnout. Profily špiček listů by se pak měly svými tvary lišit od profilů použitých třeba v 70% průměrů vrtulí.
To by snad jako připomenutí známých okolností mohlo stačit.
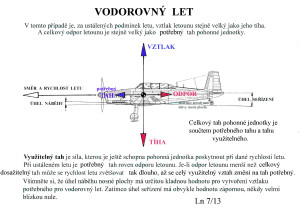
A nyní by mohly ještě napomoci následující tři obrázky, v nichž je schematicky naznačeno jaké aerodynamické síly, síly tahu a tíže působí na létající stroje (tedy i modely) ve vodorovném letu, ve svislém letu a v letu stoupavém.
Když si je pozorně prohlédnete, tak v nich najdete nemálo významných informací pro to, co se asi děje v uvedených třech fázích letů. Jsou zde již zmíněny všechny tři složky tahů jak je uvedeno v názvu tohoto článku celkový, potřebný a využitelný. Odpustil jsem si klopivý moment stroje, let s vybočením a účinnost pohonné jednotky jako celku. Naopak připomínám, že se jedná o rovnovážné ustálené stavy v daném časovém intervalu, který chceme posoudit.
Nyní dostává příležitost pokus o populární vysvětlení toho jak probíhají proměny jednotlivých složek tahů pohonné jednotky, jestliže si dodáme přiměřené odvahy a jako výchozí údaj použijeme hodnotu statického tahu.
Tah vrtulové pohonné jednotky vzniká na základě 3. Newtonova zákonu a to principu akce a reakce. To konečně platí pro jakoukoliv pohonnou jednotku létajících strojů. Jestliže se podaří uvést do pohybu nějakou vzdušnou hmotu, to je ten ohromný vítr ve vrtulovém proudu, pak energii do toho vloženou lze využít ve formě vzniklé síly opačného smyslu, kterou nazýváme tah.
Rotující vzdušný šroub, ať je to vrule, rotor, oběžné kolo dmychadla a pod., svým tvarem, průměrem a vhodným zkroucením listů (lopatek) uvede do pohybu ve směru osy otáčení právě takové množství vzduchu (nebo i jiné tekutiny), které „si to nechá líbit“. Je vhodné se o tom poučit v příslušné literatuře, kde lze nalézt několik teorií o tom, jak si takový rotující prvek počíná.
Tak vzniká tah, který je odvislý především od průměru vrtule, jejich otáček, jejího tvaru a zkroucení a použitých profilů. Takovou sílu jsme schopni rozpoznat a dokonce i poměrně snadno změřit, pokud pohonná jednotka stojí na místě. Tuto sílu nazýváme statickým tahem.
Rotující nástroj – vrtule, nassává přední stranou vzduch, prožene ho svým průřezem a vypudí směrem za sebe. Toto množství ( vzduchu) vzduchu je urychlováno z nulové rychlosti před vrtulí až k hodnotě mnohem větší rychlosti při níž opouští vrtuli.
Z 2. Newtonova zákona, který definuje sílu jako součin hmoty a jejího zrychlení, pak snadno spočítáme takto vzniklý tah, jestliže známe rychlost vrtulového proudu hned za vrtulí. Anebo můžeme ze změřeného statického tahu naopak spočítat rychlost vzduchu ve vrtulovém proudu.
Takovýto tah je často předmětem ohromného nadšení u těch, kteří to pokládají za velké vítězství ducha nad hmotou. Jenže to není tak jednoduché. Připomenu pouze známou skutečnost, že statický tah a tah získaný při malých rychlostech letu je například tím větší, čím menší je v určitém rozsahu stoupání vrtule.
A jak to nyní chápat???
Potřebným tahem je zde míněna síla, kterou potřebuje letoun k právě zvolenému pohybu, ať již v laboratoři, na ploše či za letu.
Využitelným tahem zase ta část celkového tahu, která ještě zbývá k použití. Je to tedy rezerva tahu, kterou ještě lze využít, pokud to pohonná jednotka umožní. Obvykle je pak třeba změnit počet otáček vrtule nebo její stoupání, když předpokládáme stále týž průměr.
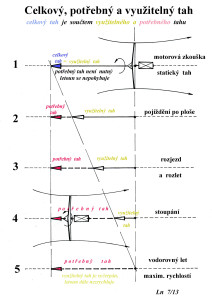
Podívejte se na následující obrázek, kde je pět možností skladeb tahu pohonné jednotky a tedy i letounu (modelu) pro zvolené situace.
1. Je to motorová zkouška, obvykle při maximálních otáčkách, při níž je zaznamenán celkový tah pohonné jednotky. Před vrtulí, dejme ve vzdálenosti větší než je asi dvojnásobek jejího průměru, není obvykle žádný pohyb vzduchu. Směrem k rotující vrtuli se však proud vzduchu začne urychlovat, až těsně před ní dosáhne přibližně poloviční hodnoty výsledné rychlosti vrtulového proudu, za ní. Celkový nárůst druhé mocniny rychlosti vzduchu urychleného vrtulí, násobený poloviční hodnotou hustoty vzduchu a ještě plochou kruhu danou jejím průměrem, dává potom sílu zvanou statický tah. Je ovšem potřeba do ní zahrnout ještě vliv účinnosti vrtule, pokud posuzujeme osamocenou vrtulovou jednotku. Pokud bychom chtěli připojit ještě vliv částí trupu za pohonnou jednotkou, pak se hodnota tahu znovu zmenší.
Předpokládejme, že máme k dispozici nějaký údaj statického tahu, který jsme třeba změřili sami nebo použili hodnot výrobce motoru s uvedením parametrů vrtule a počtu otáček.
A tuto hodnotu bychom chtěli využít k pohonu létajícího stroje.
Záměrně zde vynechávám okolnosti související například s úhly náběhu (budou větší než za letu), se kterými se vrtule musí vypořádat při statickém testu. Vrtule se stejným průměrem, ale s menším stoupáním na tom budou v tomto případě lépe než ty druhé. Změní se i otáčky, jichž bude schopna vrtule při stejném příkonu motoru vykonávat.
2. Jakmile se začne letoun po ploše pohybovat, začne k němu přicházet proud vzduchu o rychlosti dané pohybem letounu a změní se nejen otáčky vrtule, ale i úhly náběhu pod nimiž bude přicházet vzduch k listům vrtule.
K pohybu letounu (modelu) po ploše bude třeba určitý výkon, který zde zastupuje potřebný tah. O tuto hodnotu se zmenší původní celkový (statický) tah a k využití zbývá již jen jeho část, zde zvaná tah využitelný.
3. Když se začne letoun rozjíždět a postupně dosáhne rychlosti nutné pro vzlet, tak se poměry na vrtuli začnou měnit výrazněji. Zvýšená rychlost vzduchu přicházejícího k vrtuli zmenší úhly náběhu proudu vzduchu a její otáčky poněkud vzrostou. Na pohonné jednotce se nastaví jiné poměry, ve srovnání se statickým tahem. Ten je nyní zmenšen o tah potřebný ke vzletu.
4. Než přejde letoun do stoupání s optimálními parametry – rychlost letu a rychlost stoupání, bývá nutné zvýšit otáčky vrtule, aby byl získán další přírůstek potřebného tahu na úkor tahu ještě využitelného. Pokud tomu tak je a pohonná jednotka to zvládne, zbývá ještě nějaká rezerva ve využitelném tahu.
Tu je pak možné využít například k dosažení maximální či optimální rychlosti v ustáleném vodorovném letu.
Nastává případ 5 a veškerý původní tah se změní na tah potřebný a žádná rezerva zde obvykle v pohonu již nebývá.
Na tyto podmínky se navrhují vrtule a jejich geometrické parametry společně s použitými motory.
To bylo velmi zjednodušené a stručné povídání o tom jak to dopadne se statickým tahem u pevných vrtulí.
U vrtulí s možností nastavovat změnu stoupání během chodu pohonné jednotky je to jinak a účinněji.
Ti, kdo chtějí se s tím zabývat podrobněji mohou z hodnoty statického tahu a znalostí celkových součinitelů odporu stroje spočítat přibližnou hodnotu maximální rychlosti v ustáleném vodorovném letu. Celkový odpor stroje je za těchto okolností roven tahu pohonné jednotky, ať jsou k dispozici jakékoliv složky tahu.
25. 7. 2013 © Jaroslav Lněnička

So záujmom som si prečítal tento teoretický článok. Myslím si, že pri návrhu pohonu je jeho ťah zásadný parameter. Ako ho ale čo najjednoduchšie stanoviť.
Všetky doporučenia a aj modelári obyčajne vychádzajú pri výpočte pohonu z tabuľky, kde na jednej strane je typ modelu (napr. cvičný, F3A, 3D…) a na strane druhej je výkon/kg modelu.
To dáva jeden pohľad pre výpočet.
Pri výpočte treba ale zohľadniť aj jeho ťah. Nie je možné spraviť podobnú tabuľku, ale na pravej strane by bol ťah/kg modelu, alebo prenesene ťah, vyjadrený ako násobok hmotnosti modelu?
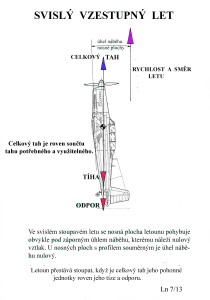
Je správne tvrdenie, že pre ustálené visenie modelu na vrtuli musí byť ťah pohonu rovný.
Ďakujem
-tabulku, kde by byl na jedné straně tah/kg by asi bylo možno udělat, ale nevím jak a já to nepoužívám
-při visení modelu by měl být tah pohonné jednotky rovný tíze modelu
– potřebný a využitelný tah vrtulové pohonné jednotky je možné pro různé režimy letů spočítat, jestliže jsou známy: rychlost letu, otáčky, přenášený výkon, průměr, počet listů vrtule a její tvar.
J.L.
Definícia visu je dôležitá a podľa toho je už možné nahrubo stanoviť potrebný ťah modelu.
Napr. 3D model – ťah omnoho väčší, ako jeho hmotnosť
cvičný hornoplošník – ťah omnoho menší, ako jeho hmotnosť
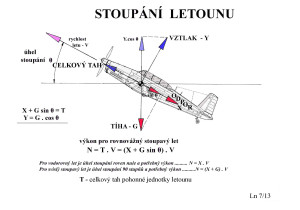
Ovšem tie slovká „omnoho väčší“, „omnoho menší“ je ešte treba kvantifikovať. Ponúkajú sa tu vzorce z obrázkov. Stanovím si max. uhol stúpania modelu a vypočítam:
1. Celkový ťah modelu zo vzorca
T= X + G sin0
alebo
2. Výkon pre rovnovážny stúpavý let zo vzorca
N = T . V = (X + G sin0) . V
3. Výkon pre zvislý stúpavý let
N = (X + G) . V ……sin0 = 1
Je tu ale jedna neznáma a to je odpor modelu X. A tu som už v koncoch.
Vzorce by mali platiť pre uhly stúpania 0 – 90°, t.j. pre vodorovný let až kolmý ustálený let hore. Ak bude nutné v kolmom lete aj zrýchlenie, ťah by mal byť ešte väčší.
Adamovič
-nezbývá než ten odpor vypočítat.
-jestli se Ti do toho nechce, tak vezmi například pro model o nosné ploše 30qdm a rychlost letu 10m/s přibližnou hodnotu odporu (1,1 – 1,4)N. Nebo pro rychlost 20m/s odpor (4,5 – 5,5)N.
To jsou jen jakési odhady, žádný solidní výpočet. Ale ve srovnání s celkovou hmotností Ti dají obraz o tom, jak to asi může fungovat, jestliže se mění rychlost a co je třeba překonávat tahem pohonné jednotky.
J.Lněnička
Tak po Vianociach som tu znova. Pre výpočet odporu modelu som vo wikipedii našiel tento vzorec:
F = C . S . ró . v2 . 1/2
C ~ 0.02 pre lietadlá
S – čelný prierez telesa
ró – hustota prostredia
v – rýchlosť
Je to vzorec, ktorým by sa dal približne vypočítať odpor modelu lietadla?
Zdraví
Adamovič
cx je celkový odpor letounu(modelu)
S je nosná plocha(křídlo)
J.L.
Dobry den pan Lněnička
rad citam Vase komentare. Tiez mam od Vas knihu Lide a letadla ktoru ste mi osobne podpisali a zaslali postou. Zaujimalo by ma ci je mozne zostrojit vrtulu ktora by fungovala ako fan o priemere 500mm a statickom tahu 75kg. Ide mi iba o staticky tah. Na prevedeni a otackach vrtule nezalezi. Co by ma este zaujimalo je aky velky prikon by potrebovala.
Dakujem
Bucuric
Stefane,
musel bych se na to podrobněji podívat. A to nějakou dobu trvá.
Těch 75 kg(/750N) se mi zdá na jednu vrtuli příliš.
J.L.
Dobry den
casu dost. Ja rad pockam.
Bucuric
Pekný článok, hľadal som informácie o ťahu elektromotora, ale prečítal som si aj toto.
Veľmi dobré obrázky, najmä ten graf „Celkový, potřebný a využitelný tah“.