V jednom z  minulých článků jsme poukázali na dvě nesmrtelné a převážně nežádoucí síly provázející aviatiku trvale. Byla to tíha a odpor tělesa pohybujícího se nějakým prostředím.

Dovolil jsem si upozornit na to, že přemrštěná snaha snižovat hmotnost v očekávání úžasných výkonů a možná i letových vlastností se může míjet účinkem, pokud se autor neseznámí důvěrněji s tím jaký je vlastně jejich skutečný vliv. V podstatě lze navázat na minulý článek.

V tomto článku upozorníme  na vliv odporu na pohyb v atmosféře Země, ale jenom jeho jedné složky vyskytující se u nosných a ocasních ploch letounů a jejich vrtulí, včetně těch co používají koptéry, rotorů vrtulníků a vírníků, oběžná kola dmychadel, ventilátorů, kompresorů, čerpadel, všelikých  turbin a podobně. Tedy všude tam, kde dochází k proudění nějaké tekutiny (plynu či kapaliny) kolem pohybujících se těles konečných rozměrů.

Ačkoliv bychom měli, tak vzhledem k populárně pojatému našemu magazínu nebudeme sáhodlouze vysvětlovat princip Bernoulliho rovnice, která v podstatě pojednává o zákonu zachování energie v proudících tekutinách.

Pouze opatrně pro některé naše čtenáře připomeneme, že jakmile dojde kdekoliv k pohybu tekutin, změní se jejich původní tlak za vzniku nevratných ztrát. Tyto změny tlaku se projeví v proměnách tlakových sil, jež tím vzniknou a působí tak ve svém okolí. Mohou-li tyto síly působit na stěny nějakých těles, které se v takovýchto skutečných proudících tekutinách nacházejí, pak vzniká odpor vždy a vztlak, o který nám v pozemské aviatice jde skoro vždy, jen někdy. Ale ty ztráty musejí být něčím nahrazeny. A protože jsou to ztráty energií jsou nahrazovány rovněž energiemi, ale z jiných zdrojů. U letounů je to například energie, kterou dodává pohonná jednotka.

Jak velký odpor či vztlak nebo následně je doprovázející i moment vzniknou, záleží na více okolnostech. Především však na vlastnostech prostředí a druhé mocnině  rychlosti proudu vůči tělesu.

My v tomto článku nejsme schopni, a mnozí čtenáři by nám to nepřipočetli k dobru, kdybychom se snažili zeširoka popisovat co se děje při proudění tekutin kdekoliv. Náš cíl je skromnější a pro stoupence aviatiky snad i  zajímavější.

Zkusme si představit nějakou pohybující se tekutinu v neomezeném prostoru nějakou rychlostí. Ta rychlost má velikost a směr. Tyto dvě fyzikální veličiny se znázorňují úsečkou ve tvaru šipky a tento geometrický obrazec je nazýván vektorem rychlosti.

Dále předpokládejme, že  si v této proudící mase zvolíme libovolnou rovinu, která je ale rovnoběžná se směrem proudění tekutiny. Podmínku rovnoběžnosti směru proudění a smyšlené v  ní roviny je nutné prozatím dodržet. Pokud je tedy směr proudění stálý a rovnoběžný s rovinou v něm smyšlenou chovají se jak proudící tekutina ( ať kapalina či plyn) tak i  smyšlená rovina k sobě celkem vlídně. Nepostrkují se, ani se nesnaží změnit svoje původní postavení. Tenká vrstva tekutiny však na rovinné desce ulpívá a tak se ji vzniklým třecím odporem snaží ve směru proudu posunout. Nic jiného by se dít nemělo.

Pokud však deska není rovinná nebo proud tekutiny změní směr či rychlost začnou se dít věci zajímavé.

Proudící tekutina začne působit na desku silami, které se ji budou snažit natočit. A to tím více, když bude nějak prohnutá.

Vedle prve zmíněného třecího odporu, který se snaží desku posunout ve smyslu proudění, vzniknou další síly způsobené změnami směru a rychlostí proudění umocněné ještě zakřiveními povrchu desky. V podstatě se jedná o dynamický účinek proudu, který je úměrný součinu měrné hmotnosti tekutiny ρ a místní rychlosti proudění  V. Je to známý vztah …….ρ÷2×V².

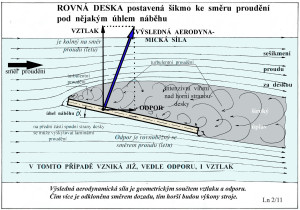
Nyní vyměníme „kulisy“ našeho pomyslného  jeviště a do proudu tekutiny   umístíme rovinnou desku. Zatím ponecháme stranou například křídlo či ocasní plochu, list rotoru či vrtule a pod. Co se stane a co se opravdu stává???

Předpokládejme na začátku pro jednoduchost, že deska zaujímá vůči směru proudění dohodnutou výchozí polohu, která je dostatečně popsána nějakým úhlem, označeným po dohodě třeba  α. Co se stane jestliže je  tento úhel rovný nule jsme popsali o několik odstavců dříve. A zachycuje to zjednodušeně následující obrázek.

Tlaky v proudící tekutině jsou nyní nad deskou stejně velké jako pod ní. Takže žádný svislá síla zde nevzniká. Je tu jen odpor – síla působící proti směru letu. A to je odpor způsobený převážně třením o povrch desky.

Když však  úhel náběhu není nulový dojde, jak jsme již předeslali prve, k výrazným změnám. A to je v obrázku dalším.

Nad deskou je nějaká rychlost horního proudu a jí odpovídající tlak a pod deskou je tlak jiný odpovídající rychlosti dolního proudu.

A tlaky nad deskou vlivem rozdílných rychlostí jsou pak  :

nahoře  ……………. ρ÷2×Vh²

dole     …………….. ρ÷2×Vd².

Jestliže bude například  horní rychlost Vh větší bude i dynamický účinek jejího proudu větší než na spodku desky.

Zde vzniká již vedle odporu i síla svislá a tou je tady aerodynamický vztlak, který je jednou z podmínek létání. Jsou tu tedy síly dvě – odpor a vztlak (zaujímají vůči sobě pravý uhel).

A sice v poměru ………….. Vh²/Vd². V jakémsi názorném příkladu tedy pro 2x větší rychlost na horní straně desky bude místní dynamický účinek proudu  4x větší než na spodní straně desky. 

Za jistých okolností ( v omezeném rozsahu úhlů náběhu) bude tedy z celkového rozdílů tlaků, nad a pod deskou, na horní straně desky  jeho podíl asi 80%-ní.

 Geometrickým součtem( což je použití věhlasné Pythagorovy věty) odporu a vztlaku je pak výsledná aerodynamická síla působící na desku. A s tou se musíme při létání vypořádávat neustále, když nechceme jenom padat.

Dejme tomu, že to je všechno asi tak, jak jsem zde napověděl. A teď zákonitě vznikne mudrlantská (  celkem správná) otázka.

A jak to vypadá v místech kde ta deska končí, když jsou tlaky nahoře a dole rozdílné????

Neumíme přeci postavit desku ( nebo křídlo, ocasní plochu, vrtuli, rotor,…) nekonečně dlouhou. Jakkoliv jsme smířeni s tím, že Vesmír je nekonečný a  kolik jich vlastně vůbec je?!

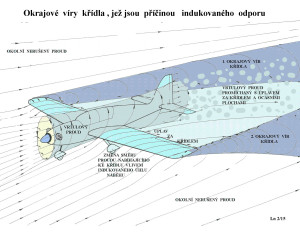
Takže co se asi děje na obou okrajích desky konečných rozměrů – křídla, když nás nyní zajímá hlavně  vzdálenost mezi jimi a tu nazýváme rozpětím.

Cokoliv ve Vesmíru a tedy i v Přírodě kolem nás má snahu nastavit, po poruše původního stavu, vhodnou rovnováhu mezi čímkoliv, ať okamžitě či po nějaké době. To se děje na úkor vložených energií za vzniku obvykle, pro probíhající děj,  nevratných ztrát.

Takže zde se snaží vyrovnat tlaky nad deskou a pod ní. Tekutina, v našem případě atmosférický vzduch, proudí z místa vyššího tlaku do míst s tlakem nižším za vzniku intenzivního víření. Tento vír má tvar jakési rotující prostorové spirály(pokud je to správný výraz)  se smyslu zprava doleva na pravém okraji křídla a ve smyslu opačném na druhém okraji. Při pohledu zezadu. Předpokládáme, že vztlak působí směrem vzhůru.

Velmi snadno to můžete demonstrovat třeba na letu modelu letadla, jehož okraje křídla jsou opatřeny tenkými papírovými pásky v délkách odpovídajících přibližně rozpětí křídla. Je to velmi instruktivní.

U velkých letounů působí tyto okrajové víry do vzdáleností několika set metrů, takže jsou pro dopravní letadla předepsány zhruba kilometrové vzdálenosti mezi nimi pokud letí po stejné trase.

     

Oba tyto okrajové víry, které vznikají nejen na okrajích křídel a ocasních ploch letounů, ale i listů vrtulí a rotorů, lopatek dmychadel, ventilátorů,…jsou příčinou vzniku intenzivního odporu. Nese název odpor indukovaný. Nevzniká pouze tehdy pokud jsou tlaky na obou stranách okraje pohybujícího tělesa stejné.

A když přijmeme za fakt, že výsledný aerodynamický odpor létajícího stroje s pevnými plochami je součtem :

1. odporu profilu

2. odporu nosné plochy a v něm především odporu indukovaného

a za   3. odporu ostatních částí a jejich vzájemných vlivů 

pak při rozboru jejich hodnot ( po nezbytném aerodynamickém výpočtu ) dojde každý kdo bude chtít k tomu, jakým dílem samy o sobě ovlivňují výsledný odpor.

Záleží na mnoha okolnostech, které to ovlivňují. Není zase však tak složité takovou analýzu udělat.

Odpor profilu by měl být znám pro potřebný rozsah letových stavů ( to je to Reynoldsovo číslo ).

Indukovaný odpor je přímo závislý na druhé mocnině součinitele vztlaku, dělené číslem 3,14 a štíhlostí nosné plochy  a to všechno násobené koeficientem, obvykle trochu větším než jedna.

Pro stejný rozsah letových stavů je potřebné získat dílčí odpory -trupu, ocasních ploch, podvozku, pohonné jednotky, všech jiných výrazně vyčnívajících částí z obrysu letounu a pod. A to všechno „svázat do pytlíčku“ a vynásobit koeficientem trochu větším než jedna. Jako prve.

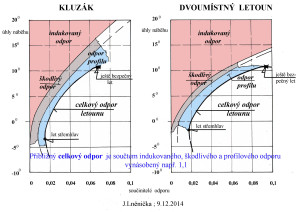
Když jsou k dispozici tyto údaje, pak je velmi vhodné je uspořádat do přehledné tabulky nebo grafu. Z nich je pak například patrné, který odpor ovlivňuje v dané letové fázi největším dílem  celkový odpor. To by mohlo být patrné z dalšího obrázku, kde je příklad odporů létajícího stroje.

A proč jsme to vlastně všechno tady dělali, když mnozí mohou namítnout, že je to již dříve v magazínu, sice odlišně, ale přesto již popsané.

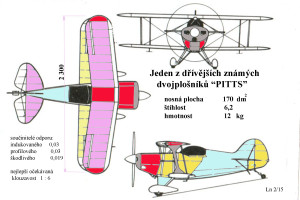
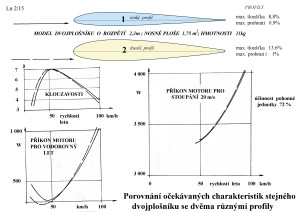
Je to například proto, aby si mnozí stoupenci aviatiky pevných ploch uvědomili, že ne vždycky je to kdovíjaká výhra použít tenčí profil v nosné ploše. Markantní je to zejména u plošníků s menšími štíhlostmi. A k tomu jsme použili jako příklad jeden z dřívějších a někdy i dodneška úspěšných strojů, který je v následující skice připomenut.

Pro něj jsem se uvolil spočítat očekávané výkony pro dva profily poměrně rozdílných tlouštěk a blízkého prohnutí, abych znovu upozornil na to, že očekávání neobvyklých výkonů jenom tím, že bude změněna tloušťka profilu nosné plochy, jsou v určité části aviatiky nenaplnitelná.

V dalším obrázku je stručný výsledek tohoto snažení, jež snad přispěje k osvětě pro více nadšenců, kteří jsou přesvědčeni, že tenčí je vždycky rychlejší.

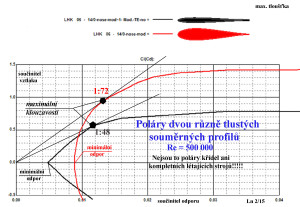
Pro ty kdo se budou chtít zamyslet trochu hlouběji uvádím ještě následují polární  diagram.

V něm jsou poláry dvou výrazně odlišných tlustých profilů. Z nich jsou patrné i velké rozdíly minimálních hodnot součinitelů odporů. Ale zároveň jsou i zřetelné ještě výraznější rozdíly v aerodynamických jemnostech ( klouzavostech) obou profilů ve prospěch toho tlustšího.

A tak je to v letectví dost často. Hledání kompromisů je hlavní činností navrhovatelů a konstruktérů letadel.

9. 2. 2015 © Jaroslav Lněnička

P.S.

Zapomněl jsem uvést přibližné tloušťky obou mých profilů označených LHK v posledním diagramu.

Ten tenčí má maximální tloušťku cca 6,5% a ten tlustší asi 16%.

9. 2. 2015 © J.Lněnička